「 This is my participation 2022 For the first time, the third challenge is 16 God , Check out the activity details ：2022 For the first time, it's a challenge 」.

The school committee said that we should roll up the built-in queue , As shown earlier, there is a simple first in and last out , First in first out queue .

The previous article showed the priority queue in the restaurant scene , And quickly explained the operation logic behind the priority queue out operation （ Use binary heap ）.

Queue out of priority queue

Do you remember how to get out of the queue ？

As shown in the figure below , This is the parent class of the queue queue.Queue Class get Method （ Take out the elements of the queue ）.

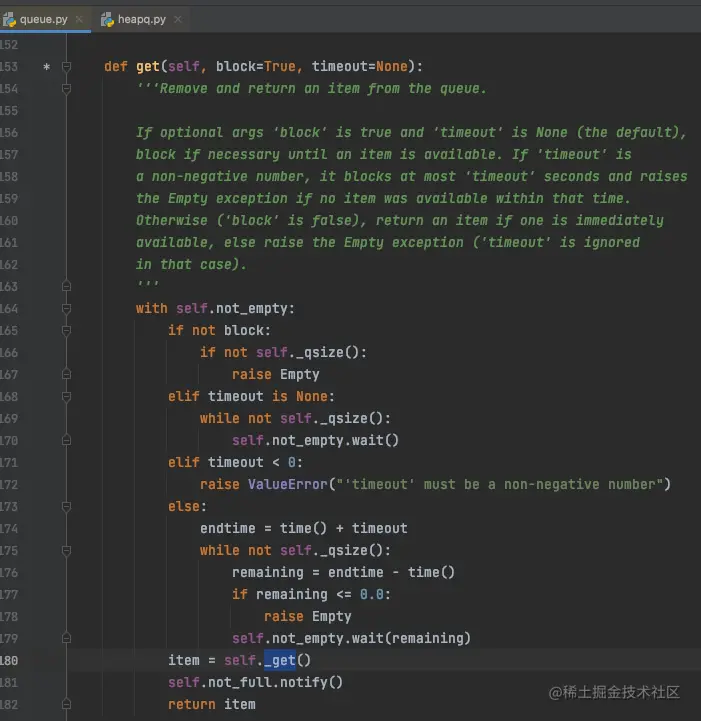
stay get The priority queue is called in the method. _get Method （ Because quilt PriorityQueue covers ）

The following is the method called by the out of queue operation of the priority queue _get

def _get(self):
return heappop(self.queue)
 Copy code 

Here is the binary stack , Let's continue to look at its implementation ：

def heappop(heap):
lastelt = heap.pop()
if heap:
returnitem = heap[0]
heap[0] = lastelt
_siftup(heap, 0)
return returnitem
return lastelt
 Copy code 

In the way ：

first line ： Pop up elements directly from the list （ Take out ）. When the entire priority queue is taken , An empty list is encountered here , The program immediately reports an error .（ Readers can generate a separate list object , direct pop. That is to say '[].pop()')

The second line ： Continue to test the list heap（ Maintain a binary stack structure ） Is it empty , If it is , Run the last line directly （ Returns the last element of the list ）, also if Statements within are not executed . There is only one element in the current list , This is the simplest .

otherwise （ The third line begins ）, Need to dynamically balance the binary tree , Make executive judgment . There are mainly two steps ：

• First step , That is, we directly remove the top node of the binary tree , Minimum heap top element priority value , The highest priority , Just take it directly .
• The second step , Replace the top element with the last element added , Directly join the remaining two subtrees . But the binary tree is not the smallest binary heap , So here comes the following method .

For the convenience of parsing , Post directly _siftup Source code here , Readers can read it quickly ：

def _siftup(heap, pos):
endpos = len(heap)
startpos = pos
newitem = heap[pos]
childpos = 2*pos + 1 # leftmost child position
while childpos < endpos:
rightpos = childpos + 1
if rightpos < endpos and not heap[childpos] < heap[rightpos]:
childpos = rightpos
heap[pos] = heap[childpos]
pos = childpos
childpos = 2*pos + 1
heap[pos] = newitem
_siftdown(heap, startpos, pos)
 Copy code 

The first three lines in the method first determine the starting position of the second , Upper left element position （childpos）, Top element newitem.

Into the loop , The exit condition here is whether the node position of the left child is => The length of the remaining list . Because every time you put in elements, you always put them in each layer from left to right .

Let's look inside the loop , The left node of the binary tree is 2pos+1, The node on the right is （2pos+1）+1.

Through this line of code ‘rightpos < endpos and not heap[childpos] < heap[rightpos]’ , It can ensure that there is always ：

The new node at the top replaces the smallest element in the left and right nodes （heap[pos] = heap[childpos]） , That is, move up the smaller value in the left and right nodes to rise to the root of the node , The following subtree satisfies the minimum binary heap condition .

Until there is no subsequent leaf node comparison .. At this time, it is equivalent to obtaining the minimum value on one side to , Put it on top and execute _siftdown Method , This has been analyzed in the previous article .

summary

Priority queue , The minimum binary heap is used as the core , It realizes efficient out of queue and in queue .

Let's show it in the drawing later , It's efficient , The priority queue mainly uses binary tree structure to deal with incoming and outgoing queues , You don't need to traverse the entire list at a time （ The specific operation efficiency is shown in the next chapter ）.

like Python Friend, , Please pay attention to Python Basic column or Python From getting started to mastering the big column

Continuous learning and continuous development , I'm Lei Xuewei ！
Programming is fun , The key is to understand the technology thoroughly .
Welcome to wechat , Like support collection !