目錄
1 電力系統環境經濟調度數學模型
2 算例——IEEE10節點
2.1 數據
2.2 Python代碼學習
3 一點拓展知識




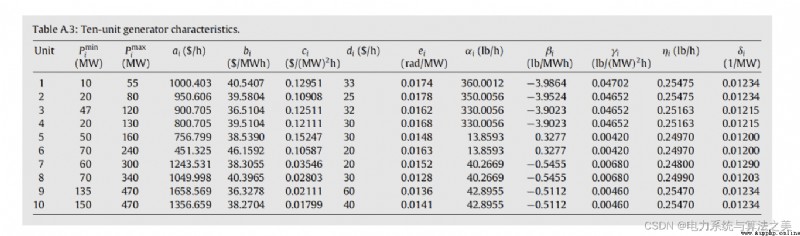
我弄成一個表格,方便編程讀寫:
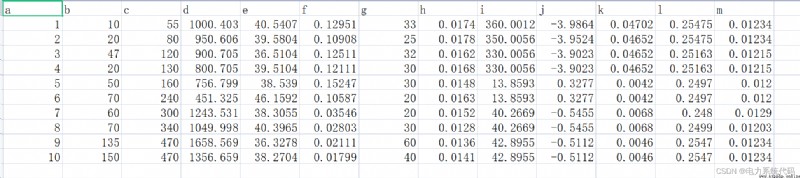
本文只展現部分代碼,全部代碼點這裡:正在為您運送作品詳情
多目標遺傳算法NSGAII在電力系統多目標問題有廣泛的應用,只要把文中的目標函數和約束條件換了,就搞定啦。
#========導入第三方庫=============
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默認字體
mpl.rcParams['axes.unicode_minus'] = False # 解決保存圖像是負號'-'顯示為方塊的問題
import matplotlib;
matplotlib.use('TkAgg')
from tqdm import tqdm # 進度條設置
# ========導入數據=============
# ~~~~~~~~~~~~~~~~~~~~~讀取文件~~~~~~~~~~~~~~~~~~~~~~
file=pd.read_csv('IEEE10.csv')#機組參數
#B=pd.read_csv('B10.csv')
#B=np.reshape()
B=np.array([[0.000049, 0.000014 ,0.000015, 0.000015, 0.000016, 0.000017 ,0.000017, 0.000018 ,0.000019, 0.00002],
[0.000014, 0.000045, 0.000016, 0.000016, 0.000017 ,0.000015, 0.000015 ,0.000016 ,0.000018, 0.000018],
[0.000015, 0.000016, 0.000039, 0.00001 ,0.000012, 0.000012 ,0.000014, 0.000014, 0.000016, 0.000016],
[0.000015, 0.000016, 0.00001, 0.00004, 0.000014 ,0.00001 ,0.000011, 0.000012, 0.000014, 0.000015],
[0.000016, 0.000017, 0.000012, 0.000014, 0.000035, 0.000011, 0.000013, 0.000013, 0.000015, 0.000016],
[0.000017, 0.000015, 0.000012, 0.00001, 0.000011 ,0.000036, 0.000012, 0.000012, 0.000014, 0.000015],
[0.000017 ,0.000015 ,0.000014, 0.000011, 0.000013, 0.000012, 0.000038, 0.000016, 0.000016, 0.000018],
[0.000018 ,0.000016, 0.000014, 0.000012, 0.000013, 0.000012, 0.000016 ,0.00004, 0.000015, 0.000016],
[0.000019 ,0.000018 ,0.000016, 0.000014, 0.000015 ,0.000014 ,0.000016, 0.000015, 0.000042 ,0.000019],
[0.00002, 0.000018 ,0.000016 ,0.000015, 0.000016, 0.000015, 0.000018 ,0.000016, 0.000019 ,0.000044]])
P_max = file['b'] #機組上限
P_min = file['c'] # #機組下限
# ~~~~~~~~~~~~~~~~~機組特性系數~~~~~~~~~~~~~~~~~~~~~~~~·
ai = file['d']
bi=file['e']
ci=file['f']
di=file['g']
ei=file['h']
# ~~~~~~~排放特性系數~~~~~~~~~~~~~~~~·
ali=file['g']
beti=file['h']
gari=file['i']
eti=file['l']
dali=file['m']
# ======多目標優化算法一次 只能求解單個時刻的解===============
class GaMultiobjective(object):
def __init__(self, Pload1, P_max, P_min, ai, bi, ci, di, ei, ali, beti, gari, eti, dali):
self.Pload1 = Pload1 # 負荷
self.P_max = P_max # 機組上限
self.P_min = P_min # 機組下限
self.ai = ai
self.bi = bi
self.ci = ci
self.di = di
self.ei = ei
self.ali = ali
self.beti = beti
self.gari = gari
self.eti = eti
self.dali = dali
# ===初始化種群====
def Initialize(self):
X = np.zeros((self.NP, 10)) # 初始化群體,10代表 個機組出力
for n in range(self.NP): # 遍歷每一個粒子
X[n, 0] = np.random.uniform(10, 55, 1)[0] # G1
X[n, 1] = np.random.uniform(20, 80, 1)[0] # G2
X[n, 2] = np.random.uniform(47, 120, 1)[0] # G3
X[n, 3] = np.random.uniform(20, 130, 1)[0] # G4
X[n, 4] = np.random.uniform(50, 160, 1)[0] # G5
X[n, 5] = np.random.uniform(70, 240, 1)[0] # G6
X[n, 6] = np.random.uniform(60, 300, 1)[0] # G7
X[n, 7] = np.random.uniform(70, 340, 1)[0] # G8
X[n, 8] = np.random.uniform(130, 470, 1)[0] # G9
X[n, 9] = np.random.uniform(150, 470, 1)[0] # G10
return X
# ==========定義目標函數、和對應的懲罰項=============
# ===定義函數1 目標函數1:系統運行成本===
def function1(self, X1):
"""
個體目標函數
:param X1: (個體[G1,G2,G3,G4,G5,G6,G7,G8,G9,G10]
:return: 函數1目標函數值
"""
SUMCOST = [] # 存儲總的成本
for i in range (9): # 遍歷每一台機組,Python是從0開始索引,0-9:10台機組
cost = self.ci[i] * X1[i] * X1[i] + self.bi[i]* X1[i] +self.ai[i]+\
np.abs(self.di[i]*np.sin(ei[i]*(self.P_min[i]-X1[i]))) #考慮閥點效應
SUMCOST.append(cost)
return np.sum(SUMCOST)
# ====定義函數2 總污染排放量====
def function2(self, X1):
"""
個體目標函數
:param X1: (個體[G1,G2,G3,G4,G5,G6,G7,G8,G9,G10]
:return: 函數2目標函數值
"""
emission=[] #儲存總的污染排放量
for i in range(9):
e=self.ali[i]+self.beti[i]*X1[i]+self.gari[i]*X1[i]*X1[i]+self.eti[i]*np.exp(self.dali[i]*X1[i])
emission.append(e)
return np.sum(emission)
# ===對應的約束 負荷平衡約束(本例子calc_e() 不起作用,已通過其它方法解決掉負荷平衡約束)===
def calc_e(self, X1):
"""
函數1 對應的個體懲罰項
:param X1: (個體[G1,G2,G3,G4,G5,G6,G7,G8,G9,G10]
:return:
"""
Ploss=0
for i in range(9):
for j in range(9):
Ploss+=X1[i]*B[i][j]*X1[j]
# cost=np.abs(X1[0]+X1[1]+X1[2]+X1[3]+X1[4]+X1[5]+X1[6]+X1[7]+X1[8]+X1[9]-np.sum(Ploss)-self.Pload1)
# return cost
return max(0,abs(sum(X1)-Ploss-Pload1-0.1))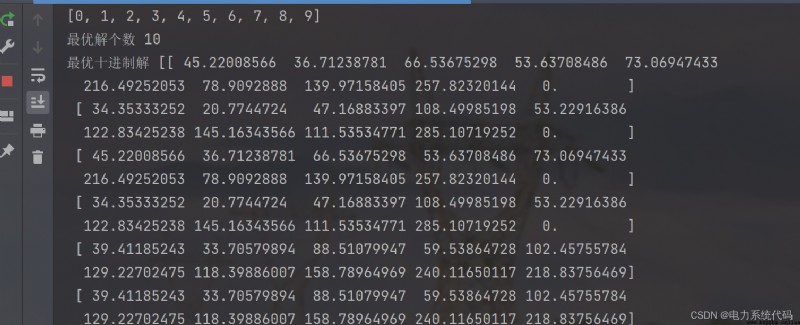
現代這種“探索、征服”的心態,從世界地圖的演變可以看得一目了然。早在歷史進到現代之前,許多文化就已經有了自己的世界地圖。當然,當時並沒有人真正知道全世界是什麼樣子,在亞非大陸上的人對美洲一無所知,美洲文化也不知道亞非大陸上的情形。但碰到不熟悉的地區,地圖上不是一筆未提,就是畫上了想象出來的怪物和奇景。這些地圖上並沒有空白的空間,讓人覺得全世界就在自己的掌握之中。
在15、16世紀,歐洲人的世界地圖開始出現大片空白。從這點可以看出科學心態的發展,以及歐洲帝國主義的動機。地圖上的空白可以說是在心理及思想上的一大突破,清楚表明歐洲人願意承認自己對於一大部分的世界還一無所知。
圖1 1459年歐洲人的世界地圖。可以看到地圖上似乎巨細靡遺,就算是當時歐洲人根
本一無所知的南非地區,都有密密麻麻的信息。
1492年,哥倫布從西班牙出發向西航行,希望能找到一條前往東亞的新航線。哥倫布當時相信的仍然是舊的世界地圖,以為全世界在地圖上一覽無遺。哥倫布從舊地圖推算,日本應該位於西班牙以西大約7000公裡遠。但事實上,從西班牙到東亞的距離要超過兩萬公裡,而且中間還隔著個他不知道的美洲大陸。1492年10月12日大約凌晨2點,哥倫布一行人與這片未知大陸有了第一次接觸。皮塔號(Pinta)的瞭望手胡安·羅德裡格斯·貝爾梅霍(Juan Rodriguez Berme jo)從桅桿上看到了現在的巴哈馬群島,高呼著:“有陸地!有陸地!”
哥倫布當時相信這個小島就位於東亞海外,屬於“Indies”(印度地方,包含今日印度、中南半島及東印度群島等地),所以他把當地人稱為“Indians”(這正是美國原住民也被稱為“印第安人”的原因)。一直到他過世,哥倫布都不認為自己犯了一個大錯。不論是對他還是許多當代的人來說,說他發現了一個完全未知的大陸,這根本難以想象。畢竟千百年來,不管是那些偉大的思想家和學者甚至是不可能犯錯的《聖經》,都只知道有歐洲、非洲和亞洲。怎麼有可能他們全錯了呢?難道《聖經》居然漏了大半個世界,只字未提?這種情況,就好像是說在1969年阿波羅11號要前往月球的途中,居然撞到了另一個從來沒人看到的月亮。而正因為哥倫布不願意接受自己的無知,我們可以說他仍然是個中世紀的人,深信著自己已經知道了全世界,所以就算已經有了如此重大的發現,也無法說服他。