預測酒店評論是好評還是差評:
1. 房間真棒,離大馬路很近,非常方便,不錯。 好評 0.9954
2. 房間有點髒,廁所還漏水,空調不制冷,下次再也不來了。 差評 0.99
3. 地板不太干淨,電視沒信號,但是空調還可以,總之還行。 好評 0.56
pip3 install nltk -i
https://pypi.tuna.tsinghua.edu.cn/simple/
pip3 install jieba -i
https://pypi.tuna.tsinghua.edu.cn/simple/
import nltk.tokenize as tk
# 把樣本按句子進行拆分 sent_list:句子列表
sent_list = tk.sent_tokenize(text)
# 把樣本按單子進行拆分 word_list:單詞列表
word_list = tk.word_tokenize(text)
# 把樣本按單詞進行拆分 punctTokenizer:分詞器對象
punctTokenizer = tk.WordPunctTokenizer()
word_list = punctTokenizer.tokenize(text)
doc = "Are you curious about tokenization? Let's see how it works! We need to analyze a couple of sentences with punctuations to see it in action."
# 分句子
sents = tk.sent_tokenize(doc)
for i in range(len(sents)):
print(i+1, ':', sents[i])
""" 1 : Are you curious about tokenization? 2 : Let's see how it works! 3 : We need to analyze a couple of sentences with punctuations to see it in action. """
# 分單詞
words = tk.word_tokenize(doc)
for i in range(len(words)):
print(i+1, ':', words[i])
""" 1 : Are 2 : you 3 : curious 4 : about 5 : tokenization 6 : ? 7 : Let 8 : 's 9 : see 10 : how 11 : it 12 : works 13 : ! 14 : We 15 : need 16 : to 17 : analyze 18 : a 19 : couple 20 : of 21 : sentences 22 : with 23 : punctuations 24 : to 25 : see 26 : it 27 : in 28 : action 29 : . """
tokenizer = tk.WordPunctTokenizer()
words = tokenizer.tokenize(doc)
for i in range(len(words)):
print(i+1, ':', words[i])
""" 1 : Are 2 : you 3 : curious 4 : about 5 : tokenization 6 : ? 7 : Let 8 : ' 9 : s 10 : see 11 : how 12 : it 13 : works 14 : ! 15 : We 16 : need 17 : to 18 : analyze 19 : a 20 : couple 21 : of 22 : sentences 23 : with 24 : punctuations 25 : to 26 : see 27 : it 28 : in 29 : action 30 : . """
This hotel is very bad. The toilet in this hotel smells bed. The environment of this hotel is very good.
This hotel is very bad.
The toilet in this hotel smells bed.
The environment of this hotel is very good.
import sklearn.feature_extraction.text as ft
# 構建詞袋模型對象
cv = ft.CountVectorizer()
# 訓練模型,把句子中所有可能出現的單詞作為特征名,每一個句子為一個樣本,單詞在句子中出現的次數為特征值
bow = cv.fit_transform(sentences).toarray()
print(bow)
# 獲取所有特征名
words = cv.get_features_names()
import sklearn.feature_extraction.text as ft
sents = ['This hotel is very bad.',
'The toilet in this hotel smells bad.',
'The environment of this hotel is very good.']
cv = ft.CountVectorizer()
bow = cv.fit_transform(sents)
print(bow)
print(bow.toarray())
print(cv.get_feature_names())
""" (0, 9) 1 (0, 3) 1 (0, 5) 1 (0, 11) 1 (0, 0) 1 (1, 9) 1 (1, 3) 1 (1, 0) 1 (1, 8) 1 (1, 10) 1 (1, 4) 1 (1, 7) 1 (2, 9) 1 (2, 3) 1 (2, 5) 1 (2, 11) 1 (2, 8) 1 (2, 1) 1 (2, 6) 1 (2, 2) 1 [[1 0 0 1 0 1 0 0 0 1 0 1] [1 0 0 1 1 0 0 1 1 1 1 0] [0 1 1 1 0 1 1 0 1 1 0 1]] ['bad', 'environment', 'good', 'hotel', 'in', 'is', 'of', 'smells', 'the', 'this', 'toilet', 'very'] """
這家酒店棒,裝修棒,早餐棒,環境棒。 1
這家酒店爛,爛爛爛,真的爛。 0
這家酒店裝修棒,服務爛。 ?
文 檔 頻 率 : D F = 含 有 某 個 單 詞 的 文 檔 樣 本 數 總 文 檔 樣 本 數 ( 與 樣 本 語 義 貢 獻 度 反 相 關 ) 文檔頻率: DF = \frac{含有某個單詞的文檔樣本數}{總文檔樣本數}(與樣本語義貢獻度反相關) 文檔頻率:DF=總文檔樣本數含有某個單詞的文檔樣本數(與樣本語義貢獻度反相關)
逆 文 檔 頻 率 : I D F = l o g ( 總 樣 本 數 1 + 含 有 某 個 單 詞 的 樣 本 數 ) ( 與 樣 本 語 義 貢 獻 度 正 相 關 ) 逆文檔頻率: IDF = log\left(\frac{總樣本數}{1+含有某個單詞的樣本數}\right)(與樣本語義貢獻度正相關) 逆文檔頻率:IDF=log(1+含有某個單詞的樣本數總樣本數)(與樣本語義貢獻度正相關)
# 構建詞袋模型對象
cv = ft.CountVectorizer()
# 訓練模型,把句子中所有可能出現的單詞作為特征名,每一個句子為一個樣本,單詞在句子中出現的次數為特征值
bow = cv.fit_transform(sentences).toarray()
# 獲取TF-IDF模型訓練器
tt = ft.TfidfTransformer()
tfidf = tt.fit_transform(bow).toarray()
tt = ft.TfidfTransformer()
tfidf = tt.fit_transform(bow).toarray()
print(np.round(tfidf, 3))
print(cv.get_feature_names())
""" [[0.488 0. 0. 0.379 0. 0.488 0. 0. 0. 0.379 0. 0.488] [0.345 0. 0. 0.268 0.454 0. 0. 0.454 0.345 0.268 0.454 0. ] [0. 0.429 0.429 0.253 0. 0.326 0.429 0. 0.326 0.253 0. 0.326]] ['bad', 'environment', 'good', 'hotel', 'in', 'is', 'of', 'smells', 'the', 'this', 'toilet', 'very'] """
import numpy as np
import pandas as pd
import sklearn.datasets as sd
import sklearn.model_selection as ms
import sklearn.linear_model as lm
import sklearn.metrics as sm
# 加載數據集
data = sd.load_files('20news', encoding='latin1')
len(data.data) # 2968個樣本
""" 2968 """
import sklearn.feature_extraction.text as ft
# 整理輸入集與輸出集 TFIDF 把每一封郵件轉成一個特征向量
cv = ft.CountVectorizer()
bow = cv.fit_transform(data.data)
tt = ft.TfidfTransformer()
tfidf = tt.fit_transform(bow)
# tfidf.shape # (2968,40605)
# 拆分測試集與訓練集
train_x, test_x, train_y, test_y = ms.train_test_split(tfidf, data.target, test_size=0.1, random_state=7)
# 交叉驗證
model = lm.LogisticRegression()
scores = ms.cross_val_score(model, tfidf, data.target, cv=5, scoring='f1_weighted')
# f1得分
print(scores.mean()) # 0.9597980963781605
# 訓練模型
model.fit(train_x, train_y)
# 測試模型,評估模型
pred_test_y = model.predict(test_x)
print(sm.classification_report(test_y, pred_test_y))
""" 0.9597980963781605 precision recall f1-score support 0 0.81 0.96 0.88 57 1 0.97 0.89 0.93 65 2 1.00 0.95 0.97 61 3 1.00 1.00 1.00 54 4 1.00 0.95 0.97 60 accuracy 0.95 297 macro avg 0.96 0.95 0.95 297 weighted avg 0.96 0.95 0.95 297 """
# 整理一組測試樣本進行模型測試
test_data = ["In the last game, the spectator was accidentally hit by a baseball injury and has been hospitalized.",
"Recently, Lao Wang is studying asymmetric encryption algorithms.",
"The two-wheeled car is pretty good on the highway."]
# 把樣本按照訓練時的方式轉換成tfidf矩陣,才可以交給模型進行預測
bow = cv.transform(test_data)
test_data = tt.transform(bow)
pred_test_y = model.predict(test_data)
print(pred_test_y)
print(data.target_names)
""" [2 0 1] ['misc.forsale', 'rec.motorcycles', 'rec.sport.baseball', 'sci.crypt', 'sci.space'] """
data.target_names
""" ['misc.forsale', 'rec.motorcycles', 'rec.sport.baseball', 'sci.crypt', 'sci.space'] """
概率是反映隨機事件出現的可能性大小. 隨機事件是指在相同條件下,可能出現也可能不出現的事件. 例如:
(1)拋一枚硬幣,可能正面朝上,可能反面朝上,這是隨機事件. 正/反面朝上的可能性稱為概率;
(2)擲骰子,擲出的點數為隨機事件. 每個點數出現的可能性稱為概率;
(3)一批商品包含良品、次品,隨機抽取一件,抽得良品/次品為隨機事件. 經過大量反復試驗,抽得次品率越來越接近於某個常數,則該常數為概率.
我們可以將隨機事件記為A或B,則P(A), P(B)表示事件A或B的概率.
指包含多個條件且所有條件同時成立的概率,記作 P ( A , B ) P ( A , B ) P(A,B) ,或 P ( A B ) P(AB) P(AB),或 P ( A ⋂ B ) P(A \bigcap B) P(A⋂B)
已知事件B發生的條件下,另一個事件A發生的概率稱為條件概率,記為: P ( A ∣ B ) P(A|B) P(A∣B)
p(下雨|陰天)
事件A不影響事件B的發生,稱這兩個事件獨立,記為:
P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)
因為A和B不相互影響,則有:
P ( A ∣ B ) = P ( A ) P(A|B) = P(A) P(A∣B)=P(A)
可以理解為,給定或不給定B的條件下,A的概率都一樣大.
先驗概率也是根據以往經驗和分析得到的概率,例如:在沒有任何信息前提的情況下,猜測對面來的陌生人姓氏,姓李的概率最大(因為全國李姓為占比最高的姓氏),這便是先驗概率.
後驗概率是指在接收了一定條件或信息的情況下的修正概率,例如:在知道對面的人來自“牛家村”的情況下,猜測他姓牛的概率最大,但不排除姓楊、李等等,這便是後驗概率.
事情還沒有發生,求這件事情發生的可能性的大小,是先驗概率(可以理解為由因求果). 事情已經發生,求這件事情發生的原因是由某個因素引起的可能性的大小,是後驗概率(由果求因). 先驗概率與後驗概率有不可分割的聯系,後驗概率的計算要以先驗概率為基礎.
貝葉斯定理由英國數學家托馬斯.貝葉斯 ( Thomas Bayes)提出,用來描述兩個條件概率之間的關系,定理描述為:
P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P ( B ) P(A|B) = \frac{P(A)P(B|A)}{P(B)} P(A∣B)=P(B)P(A)P(B∣A)
其中, P ( A ) P(A) P(A)和 P ( B ) P(B) P(B)是A事件和B事件發生的概率. P ( A ∣ B ) P(A|B) P(A∣B)稱為條件概率,表示B事件發生條件下,A事件發生的概率. 推導過程:
P ( A , B ) = P ( B ) P ( A ∣ B ) P ( B , A ) = P ( A ) P ( B ∣ A ) P(A,B) =P(B)P(A|B)\\ P(B,A) =P(A)P(B|A) P(A,B)=P(B)P(A∣B)P(B,A)=P(A)P(B∣A)
其中 P ( A , B ) P(A,B) P(A,B)稱為聯合概率,指事件B發生的概率,乘以事件A在事件B發生的條件下發生的概率. 因為 P ( A , B ) = P ( B , A ) P(A,B)=P(B,A) P(A,B)=P(B,A), 所以有:
P ( B ) P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P(B)P(A|B)=P(A)P(B|A) P(B)P(A∣B)=P(A)P(B∣A)
兩邊同時除以P(B),則得到貝葉斯定理的表達式. 其中, P ( A ) P(A) P(A)是先驗概率, P ( A ∣ B ) P(A|B) P(A∣B)是已知B發生後A的條件概率,也被稱作後驗概率.
假設一個學校中 60%的男生 和40%的女生 ,女生穿褲子的人數和穿裙子的人數相等,所有的男生都穿褲子,一個人隨機在遠處眺望,看一個穿褲子的學生,請問這個學生是女生的概率:
p(女) = 0.4
p(褲子|女) = 0.5
p(褲子) = 0.8
P(女|褲子) = 0.4 * 0.5 / 0.8 = 0.25
P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P ( B ) P(A|B) = \frac{P(A)P(B|A)}{P(B)} P(A∣B)=P(B)P(A)P(B∣A)
import sklearn.naive_bayes as nb
# 創建高斯樸素貝葉斯分類器對象
model = nb.GaussianNB()
model = nb.MultinomialNB()
model.fit(x, y)
result = model.predict(samples)
GaussianNB 更適合服從高斯分布的訓練樣本
MultinomialNB 更適合服從多項分布的訓練樣本
在sklearn中,提供了三個樸素貝葉斯分類器,分別是:
該示例中,樣本的值為連續值,且呈正態分布,所以采用GaussianNB模型. 代碼如下:
# 樸素貝葉斯分類示例
import numpy as np
import sklearn.naive_bayes as nb
import matplotlib.pyplot as mp
# 輸入,輸出
x, y = [], []
# 讀取數據文件
with open("../data/multiple1.txt", "r") as f:
for line in f.readlines():
data = [float(substr) for substr in line.split(",")]
x.append(data[:-1]) # 輸入樣本:取從第一列到倒數第二列
y.append(data[-1]) # 輸出樣本:取最後一列
x = np.array(x)
y = np.array(y, dtype=int)
# 創建高斯樸素貝葉斯分類器對象
model = nb.GaussianNB()
model.fit(x, y) # 訓練
# 計算顯示范圍
left = x[:, 0].min() - 1
right = x[:, 0].max() + 1
buttom = x[:, 1].min() - 1
top = x[:, 1].max() + 1
grid_x, grid_y = np.meshgrid(np.arange(left, right, 0.01),
np.arange(buttom, top, 0.01))
mesh_x = np.column_stack((grid_x.ravel(), grid_y.ravel()))
mesh_z = model.predict(mesh_x)
mesh_z = mesh_z.reshape(grid_x.shape)
mp.figure('Naive Bayes Classification', facecolor='lightgray')
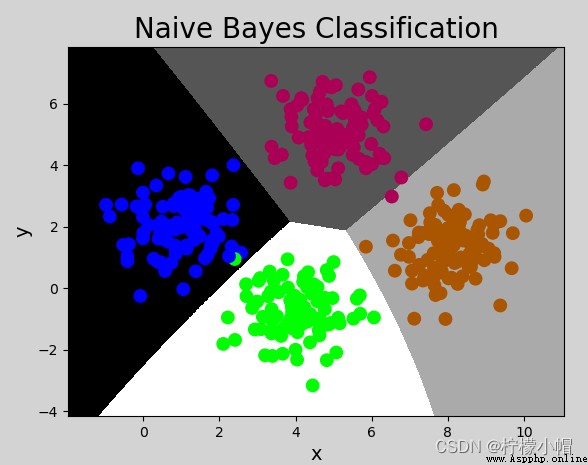
mp.title('Naive Bayes Classification', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x, grid_y, mesh_z, cmap='gray')
mp.scatter(x[:, 0], x[:, 1], c=y, cmap='brg', s=80)
mp.show()
import numpy as np
import pandas as pd
import sklearn.datasets as sd
import sklearn.model_selection as ms
import sklearn.linear_model as lm
import sklearn.metrics as sm
# 加載數據集
data = sd.load_files('20news', encoding='latin1')
import sklearn.feature_extraction.text as ft
# 整理輸入集與輸出集 TFIDF 把每一封郵件轉成一個特征向量
cv = ft.CountVectorizer()
bow = cv.fit_transform(data.data)
tt = ft.TfidfTransformer()
tfidf = tt.fit_transform(bow)
# tfidf.shape # (2968,40605)
# 拆分測試集與訓練集
train_x, test_x, train_y, test_y = ms.train_test_split(tfidf, data.target, test_size=0.1, random_state=7)
# 交叉驗證
# 使用樸素貝葉斯
import sklearn.naive_bayes as nb
model = nb.MultinomialNB()
scores = ms.cross_val_score(model, tfidf, data.target, cv=5, scoring='f1_weighted')
# f1得分
print(scores.mean())
# 訓練模型
model.fit(train_x, train_y)
# 測試模型,評估模型
pred_test_y = model.predict(test_x)
print(sm.classification_report(test_y, pred_test_y))
""" 0.9458384770112502 precision recall f1-score support 0 1.00 0.84 0.91 57 1 0.94 0.94 0.94 65 2 0.95 0.97 0.96 61 3 0.90 1.00 0.95 54 4 0.97 1.00 0.98 60 accuracy 0.95 297 macro avg 0.95 0.95 0.95 297 weighted avg 0.95 0.95 0.95 297 """
# 整理一組測試樣本進行模型測試
test_data = ["In the last game, the spectator was accidentally hit by a baseball injury and has been hospitalized.",
"Recently, Lao Wang is studying asymmetric encryption algorithms.",
"The two-wheeled car is pretty good on the highway.",
"Next year, China will explore Mars."]
# 把樣本按照訓練時的方式轉換成tfidf矩陣,才可以交給模型進行預測
bow = cv.transform(test_data)
test_data = tt.transform(bow)
pred_test_y = model.predict(test_data)
print(pred_test_y)
print(data.target_names)
""" [2 3 1 4] ['misc.forsale', 'rec.motorcycles', 'rec.sport.baseball', 'sci.crypt', 'sci.space'] """
① 優點
② 缺點