1 題目

在二維空間中有許多球形的氣球。對於每個氣球，提供的輸入是水平方向上，氣球直徑的開始和結束坐標。由於它是水平的，所以縱坐標並不重要，因此只要知道開始和結束的橫坐標就足夠了。開始坐標總是小於結束坐標。

一支弓箭可以沿著 x 軸從不同點完全垂直地射出。在坐標 x 處射出一支箭，若有一個氣球的直徑的開始和結束坐標為 x s t a r t ， x e n d x_{start}，x_{end} xstart​，xend​， 且滿足 x s t a r t ， ≤ x ≤ x e n d x_{start}，≤ x ≤ x_{end} xstart​，≤x≤xend​，則該氣球會被引爆。可以射出的弓箭的數量沒有限制。 弓箭一旦被射出之後，可以無限地前進。我們想找到使得所有氣球全部被引爆，所需的弓箭的最小數量。

給你一個數組 points ，其中 p o i n t s [ i ] = [ x s t a r t , x e n d ] points [i] = [x_{start},x_{end}] points[i]=[xstart​,xend​]，返回引爆所有氣球所必須射出的最小弓箭數。

2 解析

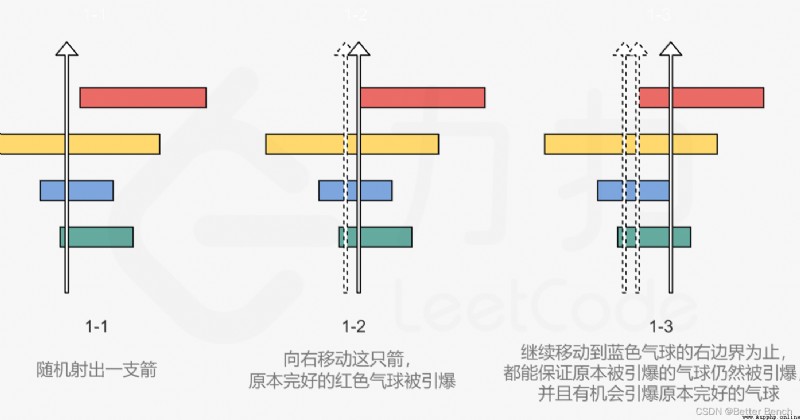
考慮所有氣球中右邊界位置最靠左的那一個，那麼一定有一支箭的射出位置就是它的右邊界（否則就沒有箭可以將其引爆了）。當我們確定了一支箭之後，我們就可以將這支箭引爆的所有氣球移除，並從剩下未被引爆的氣球中，再選擇右邊界位置最靠左的那一個，確定下一支箭，直到所有的氣球都被引爆。

3 python 實現

def findMinArrowShots(self, points: List[List[int]]) -> int:
if not points:
return 0
# 第一步，先將原數組進行一個排序的操作，將右端排序
points.sort(key = lambda x:x[1])
#右端最小的球
pos = points[0][1]
# 注意初始化是1，因為任意一針都可以射到一個氣球
ans = 1
for p in points:
# 如果某個氣球的左邊界在最小的右邊界內，則這個氣球就可以被射到
if p[0]>pos:
# 更新最小的右邊界
pos = p[1]
ans +=1
return ans