python Kalman濾波跟蹤（鏈接整理+理解）

Kalman濾波器真的太復雜了，因此整理了這篇文章，來記錄一下對自己有用的一些參考鏈接。
如果用我自己的話來總結kalman濾波器（可能不准確）：

1. 要觀測的目標自身存在一個運動狀態（狀態方程）；
2. 在這個目標身上我安裝了一些傳感器（觀測方程）；
3. 我可以通過它上一個的運動狀態，來預測此時刻的位置；
4. 我也可以通過傳感器來直接檢測出它此時刻的位置；
5. 但是這個世界存在著誤差，我無論預測還是檢測都可能不准；
6. 因此我打算將預測值和檢測值數據融合一下；
7. 在數據融合過程中，我更相信預測值還是檢測值，那就用到卡爾曼增益（K_k）;
8. Kalman幫我決定更相信預測值還是檢測值進行了量化，Kalman根據協方差矩陣、狀態觀測矩陣等寫出了一個方程，讓估計誤差最小。

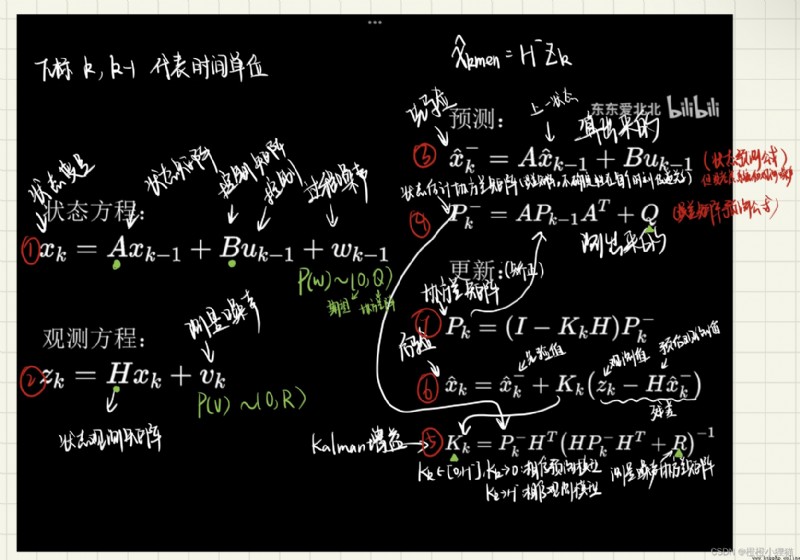
Kalman跟蹤直觀感受

鏈接說明用卡爾曼濾波器打造一個簡易單目標跟蹤器

Kalman原理

鏈接說明授之以漁： 卡爾曼濾波器 …大瀉蜜 …一個段子，啥都沒記住就記住了這個哈哈【卡爾曼濾波器】1_遞歸算法_Recursive Processing對卡爾曼原理解說的視頻，方便入門，也適合二刷三刷目標跟蹤之卡爾曼濾波—理解Kalman濾波的使用預測對狀態方程和觀測方程進行了比較詳細的解說。圖像處理之目標跟蹤（一）之卡爾曼kalman濾波跟蹤（主要為知識梳理）（轉載）對預測和更新方程進行了比較詳細的說明，但是寫得比較凌亂如何快速理解卡爾曼濾波跟蹤 python 目標跟蹤算法對預測和更新方程進行了比較詳細的說明，但是寫得比較凌亂

Kalman應用

鏈接說明卡爾曼濾波在目標跟蹤中的運用python中卡爾曼濾波的案例以及調用opencv自帶庫的寫法學習OpenCV2——卡爾曼濾波(KalmanFilter)詳解待讀使用Kalman濾波器做目標跟蹤待讀

opencv官方kalman函數說明
cv::KalmanFilter Class Reference

自己寫了個類
輸入值為目標的中心坐標和長寬，輸入預測的坐標位置和速度，可能存在部分錯誤，需後期修正。

import cv2
import numpy as np
# from myUtils.utils import xyxy_to_xywh
class KalmanTrack:
def __init__(self):
# 狀態數和觀測數需要修改
self.kalman = cv2.KalmanFilter(6, 4) # 6：狀態數，包括（xmin，ymin，xmax，ymax, dx，dy）坐標及速度（每次移動的距離）；
# 4：觀測量，能看到的是坐標值
# 狀態轉移矩陣
A = np.array([[1, 0, 0, 0, 1, 0],
[0, 1, 0, 0, 0, 1],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 1]], np.float32)
self.kalman.transitionMatrix = A # 狀態轉移矩陣
# 控制矩陣
B = None
self.kalman.controlMatrix = B
# 狀態觀測矩陣
H = np.array([[1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0]], np.float32)
self.kalman.measurementMatrix = H # 系統測量矩陣
# 觀測噪聲協方差矩陣R，p(v)~N(0,R)
# 觀測噪聲來自於檢測框丟失、重疊等
R = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]], np.float32)
self.kalman.measurementNoiseCov = R
# 過程噪聲協方差矩陣Q，p(w)~N(0,Q)，噪聲來自真實世界中的不確定性,
# 在跟蹤任務當中，過程噪聲來自於目標移動的不確定性（突然加速、減速、轉彎等）
Q = np.eye(6, dtype=np.float32) * 0.1
self.kalman.processNoiseCov = Q
# 狀態估計協方差矩陣P初始化
P = np.eye(6, dtype=np.float32)
self.kalman.errorCovPre = P
self.cur_measurement = np.nan
self.cur_prediction = np.nan
self.pre_measurement = np.nan
self.pre_prediction = np.nan
def get_cur_state(self, target_box):
"""獲取初始值狀態測量值"""
# target_box = [729, 238, 764, 339]
self.cur_measurement = target_box # 目標初始bouding box
# self.cur_measurement = xyxy_to_xywh(self.cur_measurement)
# [中心x,中心y,寬w,高h]
self.cur_measurement = np.array(
[[np.float32(self.cur_measurement[0]), np.float32(self.cur_measurement[1]),
np.float32(self.cur_measurement[2]), np.float32(self.cur_measurement[3])]]).T
return self.cur_measurement
def get_initial_state(self, target_box):
self.cur_measurement = self.get_cur_state(target_box)
self.pre_measurement = self.cur_measurement
self.cur_prediction = self.cur_measurement
self.pre_prediction = self.cur_measurement
def correct_and_predict(self, target_box):
# 將前線狀態進行存儲
self.pre_measurement = self.cur_measurement
self.pre_prediction = self.cur_prediction
# 用當前測量來校正卡爾曼濾波器
self.cur_measurement = self.get_cur_state(target_box)
self.kalman.correct(self.cur_measurement) # 用當前測量來校正卡爾曼濾波器
self.cur_prediction = self.kalman.predict() # 計算卡爾曼預測值，作為當前預測
return self.cur_prediction
if __name__ == '__main__':
kalman_tracker = KalmanTrack()
kalman_tracker.get_initial_state([729, 288, 35, 101]) # xywh
while True:
# 將先前的預測值作為當前的測量值
data = list([kalman_tracker.pre_prediction[0][0], kalman_tracker.pre_prediction[1][0],
kalman_tracker.pre_prediction[2][0], kalman_tracker.pre_prediction[3][0]])
print(kalman_tracker.correct_and_predict(data))