Python Kalman filter tracking (link sorting + understanding)

Kalman The filter is really too complicated , So I organized this article , To record some useful reference links .
If I use my own words to sum up kalman filter （ May not be accurate ）：

1. The target to be observed has a motion state （ Equation of state ）;
2. I installed some sensors on this target （ The observation equation ）;
3. I can use the motion state of the previous one , Come on forecast The position of this moment ;
4. I can also use sensors to directly testing The position at this moment ;
5. But there are errors in the world , I may not be able to predict or test ;
6. So I'm going to fuse the predicted value with the detected value ;
7. In the process of data fusion , I prefer the predicted value to the detected value , Then use the Kalman gain （K_k）;
8. Kalman Help me decide whether I believe in the predicted value or the measured value ,Kalman According to the covariance matrix 、 State observation matrix, etc. write an equation , Minimize the estimation error .

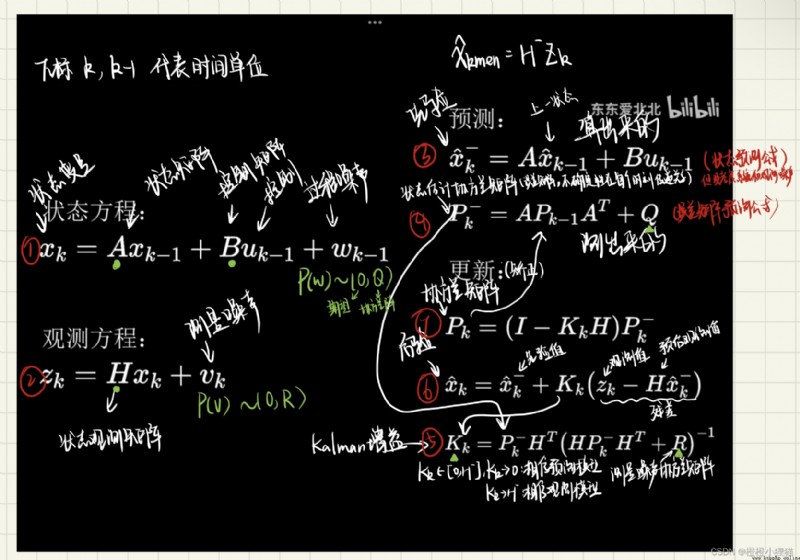
Kalman Track intuitive feelings

link explain Build a simple single target tracker with Kalman filter

Kalman principle

link explain Teach to fish ： Kalman filter … Diarrhea honey … A passage , I remember this without remembering anything 【 Kalman filter 】1_ A recursive algorithm _Recursive Processing Video explaining the principle of Kalman , Easy to get started , It is also suitable for two brushes and three brushes Kalman filter for target tracking — understand Kalman The use of filtering predicts The state equation and observation equation are explained in detail . Target tracking in image processing （ One ） It's Kalman kalman Filter tracking （ It mainly combs the knowledge ）（ Reprint ） The prediction and updating equations are explained in detail , But it's messy How to quickly understand Kalman filter tracking python Target tracking algorithm The prediction and updating equations are explained in detail , But it's messy

Kalman application

link explain Application of Kalman filter in target tracking python Kalman filter in the case and call opencv How to write the self-contained Library Study OpenCV2—— Kalman filtering (KalmanFilter) Detailed explanation To be read Use Kalman Filter for target tracking To be read

opencv official kalman Function description
cv::KalmanFilter Class Reference

I wrote a class myself
The input values are the center coordinates, length and width of the target , Enter the predicted coordinate position and speed , There may be some errors , It needs to be revised later .

import cv2
import numpy as np
# from myUtils.utils import xyxy_to_xywh
class KalmanTrack:
def __init__(self):
# The number of States and observations needs to be modified 
self.kalman = cv2.KalmanFilter(6, 4) # 6： Number of States , Include （xmin,ymin,xmax,ymax, dx,dy） Coordinates and speed （ The distance of each move ）;
# 4： Observation and measurement , What you can see is the coordinate value 
# State transition matrix 
A = np.array([[1, 0, 0, 0, 1, 0],
[0, 1, 0, 0, 0, 1],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 1]], np.float32)
self.kalman.transitionMatrix = A # State transition matrix 
# Control matrix 
B = None
self.kalman.controlMatrix = B
# State observation matrix 
H = np.array([[1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0]], np.float32)
self.kalman.measurementMatrix = H # System measurement matrix 
# Observation noise covariance matrix R,p(v)~N(0,R)
# The observation noise comes from the loss of detection frame 、 Overlap, etc. 
R = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]], np.float32)
self.kalman.measurementNoiseCov = R
# Process noise covariance matrix Q,p(w)~N(0,Q), Noise comes from uncertainty in the real world ,
# In the tracking task , The process noise comes from the uncertainty of target movement （ A sudden acceleration 、 Slow down 、 Turn, etc ）
Q = np.eye(6, dtype=np.float32) * 0.1
self.kalman.processNoiseCov = Q
# Covariance matrix of state estimation P initialization 
P = np.eye(6, dtype=np.float32)
self.kalman.errorCovPre = P
self.cur_measurement = np.nan
self.cur_prediction = np.nan
self.pre_measurement = np.nan
self.pre_prediction = np.nan
def get_cur_state(self, target_box):
""" Get the initial value state measurement value """
# target_box = [729, 238, 764, 339]
self.cur_measurement = target_box # Target initial bouding box
# self.cur_measurement = xyxy_to_xywh(self.cur_measurement)
# [ center x, center y, wide w, high h]
self.cur_measurement = np.array(
[[np.float32(self.cur_measurement[0]), np.float32(self.cur_measurement[1]),
np.float32(self.cur_measurement[2]), np.float32(self.cur_measurement[3])]]).T
return self.cur_measurement
def get_initial_state(self, target_box):
self.cur_measurement = self.get_cur_state(target_box)
self.pre_measurement = self.cur_measurement
self.cur_prediction = self.cur_measurement
self.pre_prediction = self.cur_measurement
def correct_and_predict(self, target_box):
# Store the front line status 
self.pre_measurement = self.cur_measurement
self.pre_prediction = self.cur_prediction
# Use the current measurement to correct the Kalman filter 
self.cur_measurement = self.get_cur_state(target_box)
self.kalman.correct(self.cur_measurement) # Use the current measurement to correct the Kalman filter 
self.cur_prediction = self.kalman.predict() # Calculate the Kalman prediction value , As a current forecast 
return self.cur_prediction
if __name__ == '__main__':
kalman_tracker = KalmanTrack()
kalman_tracker.get_initial_state([729, 288, 35, 101]) # xywh
while True:
# Take the previous predicted value as the current measured value 
data = list([kalman_tracker.pre_prediction[0][0], kalman_tracker.pre_prediction[1][0],
kalman_tracker.pre_prediction[2][0], kalman_tracker.pre_prediction[3][0]])
print(kalman_tracker.correct_and_predict(data))