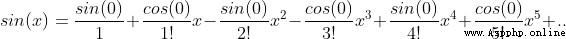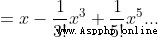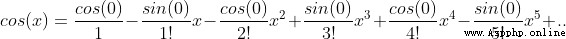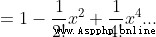The content of this article comes from learning MIT open class ： Single Variable Calculus - Taylor's series - Netease public class
Bullseye： Unit one use python Learning Calculus （ One ） Installation development environment Anaconda and derivative （ On ）- 1/x The derivative of
Centroid problem Center of Mass - Sciencetopia
The problem of focus Center of Gravity Definition, Equation and Calculation
Bullseye： Unit one use python Learning Calculus （ Two ）VSCode 、PYGame and derivative （ On ）- Instantaneous speed
Catalog
One 、 Center of gravity and center of mass
1、 centroid
（1） An object
（2） System centroid ：
2、 Focus
（1） Single object
（2） Center of gravity of the system ：
3、 Center of gravity positions of different shapes
Two 、 The problem of focus
1、 experiment
2、 Consider this problem with the idea of series , The teacher's thought experiment
（1） Set up
（2） Calculation
（3） Calculation spans 26 How many pieces of wood do you need to stack for a unit length distance ？
（4） The teacher asked for attention , Although this series has no limit , But the growth of this series is very slow .
3、 ... and 、 Power series
1、 Geometric series （Geomeric Series）
（1） prove
2、 The general form of power series
（1） The formula
（2） How to determine
3、 The law of convergence of power series （ Similar to polynomials ）
4、 Taylor formula （Taylor's Formula）
5、 The application of Taylor formula （ seek e ）
6、 seek sin(x)
7、 seek cos(x)
A rigid body is made up of a large number of particles , The mass of a rigid body is the sum of the masses of individual particles . however , We can consider a point on an object , So that all the mass of the object is concentrated on it , And when the same force is applied , The motion of this point is the same as that of a particle with the same mass as the object . This point is called the center of mass . therefore , The center of mass of an object is the point where the applied force produces linear acceleration but does not rotate .
The force on a single object is the sum of the forces on each particle above it
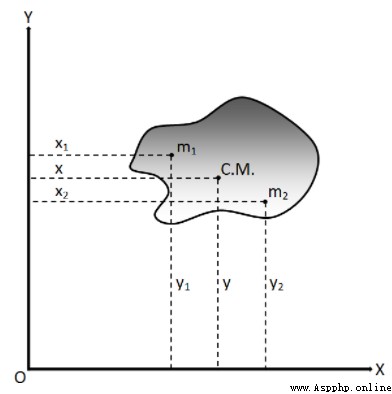
Set up ： As shown in the figure, the total mass is M; The center of mass is C.M.; 'm1, m2 ...' Is the mass of a point on an object
Centroid formula （center of mass [x, y]）=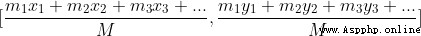 
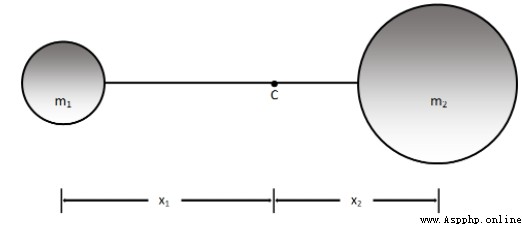
Set up ： The two masses are m1 and m2 The object , As shown in the figure . Let the mass be connected by a rigid rod , And let C Is their center of mass .
There's a formula ：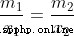 
The center of gravity is the point where the weight of the object acts and the total gravitational torque on the object is zero , Abbreviation C.G.
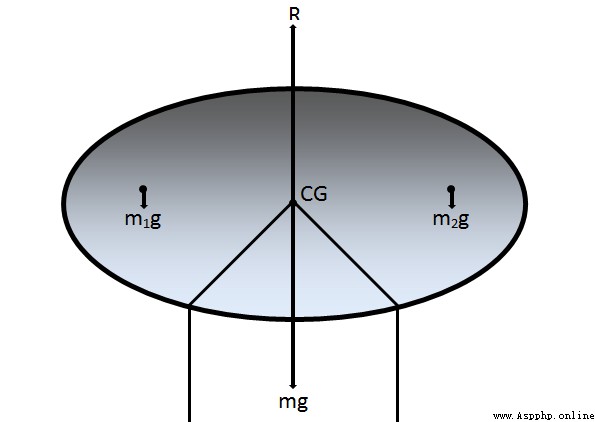
Set up ： The gravity of a particle on a body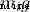 
, 
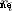It's this particle from the cardboard CG The position vector of , 
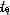It's the torque of gravity on this particle
We know that CG The total point gravity torque is 0, So there is
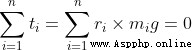
because g Is constant ,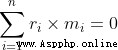 
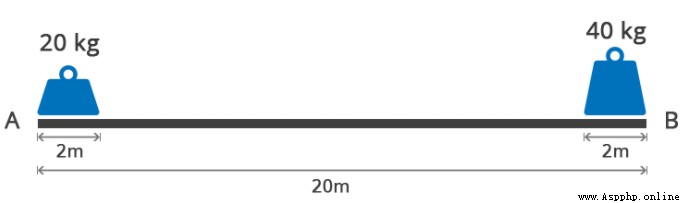
Set up ： Two widths 2m Iron block a, b, The difference is heavy 20kg,40kg, And placed on both sides of the board A、B, The board is long 20m.
a Center of gravity distance A spot 1m, and b Center of gravity distance A spot 19m
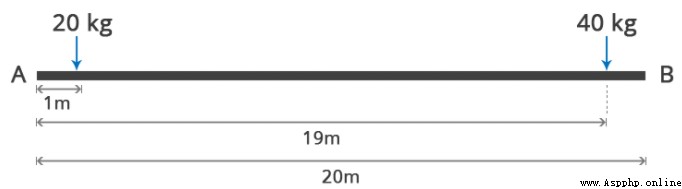
To the left A Point as a benchmark
Center of gravity of the system = Total gravity torque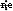 
Total arm of force = （A The arm of force 
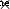A Point force + B The arm of force 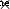B Point force 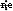） （A Point force + B Point arm ）
Total gravity torque =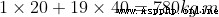 
The center of gravity of the system is to the left =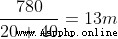 
size
CG Location
Thin uniform strips
The midpoint of the bar
ring
The center of the ring
The disk
Disk center
sphere 、 Hollow sphere 、 Annular disc
In the center of it
Cube or rectangular block
The intersection of diagonals
The triangle
The intersection of the center lines
Square layer 、 Parallelogram and rectangular layer
The intersection of diagonals
Cylinder
The midpoint of the axis
A cone or pyramid
On the line connecting with the center vertex of the bottom surface , The distance from the bottom is equal to the length of the line 1/4
Pictured , There are many building blocks together , Bottom up , Each piece is offset to the left by a certain distance , Ask if the right measurement of the top block can be shifted to the left measurement of the bottom block .
The teacher did the experiment with several building blocks , And succeeded in . The secret here is to arrange it from top to bottom .
The principle is , As long as there is support at the center of gravity of the building block , Building blocks can stand .
The center of gravity of the first building block is at its center , So the second block should be placed in half of the first block （ The building blocks are of equal size , So we only need to consider the horizontal position ,xCenter1）. The first and second building blocks form a new system , The center of gravity of the system is at the average position of the original center of gravity of the first block and the second block （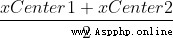 
）, And so on n When blocks are laid out in this way , The center of gravity of their system is ( 
)
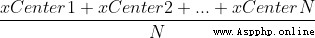Simulation program ：
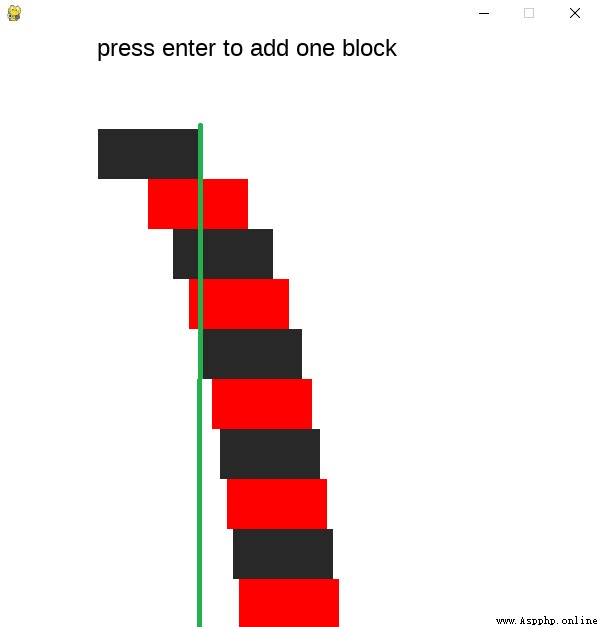
pygame Based on the simulation program
link ： Baidu SkyDrive Please enter the extraction code
Extraction code ：1g1u
decompression 7z, And run in the extracted directory AddRectangles.py. Click enter in the program to add a building block .
and 
The average of . Because the weight of each building block is equal , Is the first n Blocks have accumulated n Weight of , and n+1 Blocks have weight 1, Their average value is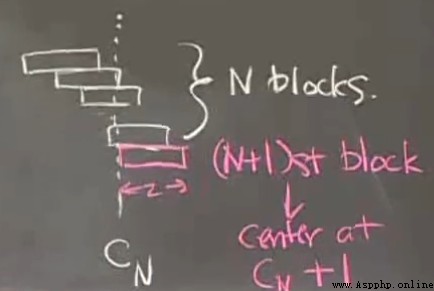 
Consider the formula of the center of gravity of the system in the center of gravity
Based on the origin ,
Center of gravity of the system = Total gravity torque 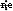Total arm of force = （A The arm of force 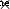A Point force + B The arm of force 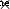B Point force 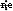） （A Point force + B Point arm ）
That is the first. n+1 The left side of the block is in front n The center of gravity of the block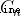 
（W=1, Gravity is n ） below , That is to say, No n+1 The center of gravity of the block is 
（ Gravity is 1 ）
Take the weight into account , Then the new focus is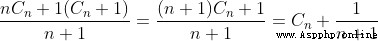 
Program ：
import numpy as np
from sympy import *
import matplotlib.pyplot as plt
def GetCenter(steps, weight, length):
Cn = 0
for i in range(steps):
n = i
Cn = (Cn*weight*n + (Cn + length/2.0)*weight)/(n+1)
print(Cn)
W = 1
L = 2
GetCenter(100,weight=W,length =L)
1.0
1.5
1.8333333333333333
2.083333333333333
2.2833333333333328
...
5.177377517639616
5.187377517639615Expand by formula ：
....
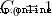
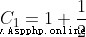
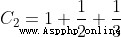
It is known from the previous chapter that ：
Bullseye： Unit 5 use python Learning Calculus （ Thirty-three ） Anomalous integral （ Next ）-- Infinite series and convergence criterion
Riemannian upper sum （ 
）
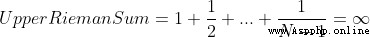
Obviously this 
（ Diverging ）
From the knowledge in the previous chapter , 
Approximate and less than （
）,
Pay attention here , Each block is defined as 2 Unit distance , So when we need to cross 26 Unit distance ,
First of all, subtract the bottom piece 2 Unit distance , Then is the distance from the center of gravity of the rest of the building blocks to the target position, that is 24 Unit distance , That is to say 
, because 
, That is to say, let the 24 This is the unit distance n The center of gravity of the block , seek n+1（ obviously n Is an integer ）.
x = symbols('x')
eq = ln(x)-24
eq1 = Eq(eq,0)
solveX = solve(eq1)
print(int(solveX[0]))
26489122129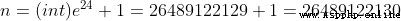
Suppose the wood block is high 3cm, How high are these wooden blocks piled up ？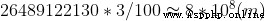 
, About the distance from the earth to the moon 2 times
When |x| < 1
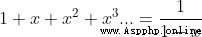
Suppose there is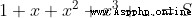 
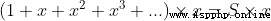
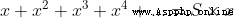
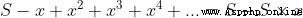
because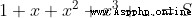
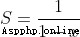
This certification requires S First, there must be , That is, if this power series converges , It cannot be divergent .
When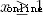 
when , equation 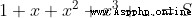Will become 
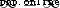, The result is meaningless .
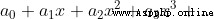
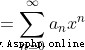
( The radius of convergence radius of converges)
（ Series convergence point set interval ）
When R" class=mathcode src="//img.inotgo.com/imagesLocal/202206/28/202206280438092099_19.gif"> ,
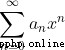It's divergent
When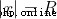 
, Is the boundary , Will not be used
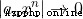Tending at an exponential rate 0 , When
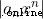Will not tend to 0 , When R" class=mathcode src="//img.inotgo.com/imagesLocal/202206/28/202206280438092099_19.gif">
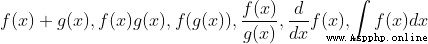These operations are valid for power series
（1） Examples of operations
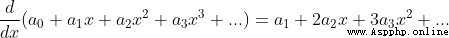
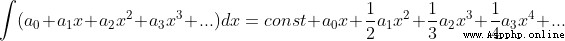
Be careful ： When using Taylor's formula , When n=0 when , conventional 0! = 1
The essence of Taylor's formula is approximation , When f(x) stay 
There is n Derivative, , Then there is a function that can be approximated by a power function , There's a formula
When this function is in x=0 There is n Derivative, , Taylor's formula is transformed into the more commonly used McLaughlin's formula
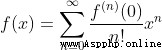
When this expansion n The bigger the value is. , The higher the approximation
Usually in power series ,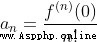 
prove ：
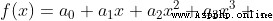
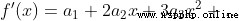
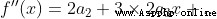
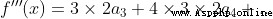
x take 0,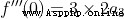 
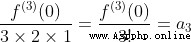
We know , When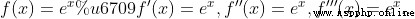 
,
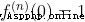
So we can bring it into Taylor's formula , Yes
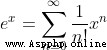
and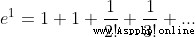 
We know , When 
