One 、 The history of Hamiltonian problem

         Hamiltonian path problem in the early 1970s , It turned out to be “NP Completely ” Of . It is said that problems of this nature , It's hard to find an effective algorithm . In fact, for some vertices less than 100 Network of , Using the best algorithms and computers available also takes absurd time （ For example, hundreds of years ） To determine whether there is such a path .

Two 、 Definition of Hamiltonian cycle in graph theory

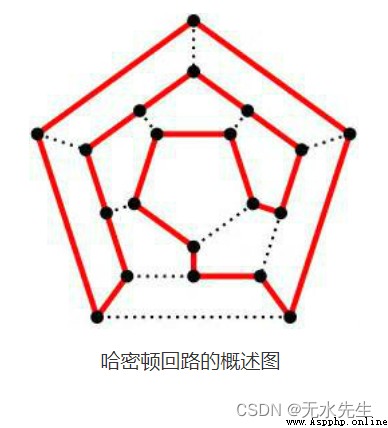
         Definition of Hamiltonian circuit ： G=(V,E) It's a picture , if G A path passes through each vertex only once , Call this path Hamiltonian path . if G A loop in the passes through and only passes through each vertex once , Call this ring Hamiltonian loop . If a graph has a Hamiltonian loop , It is called Hamiltonian graph .

3、 ... and 、 Depth-first traversal （Depth First Search, abbreviation DFS）

         The main idea of depth first traversal is from an unreachable vertex in the graph V Start , Go all the way to the end , Then back from the node at the end of the road to the previous node , Start from another road to the end …, Repeat this process recursively , Until all the vertices are traversed , It is characterized by not hitting the south wall and not looking back , Go one way first , Another way to go .

         To find the Hamiltonian loop , We will use backtracking and DFS To traverse all possible different types of Hamiltonian paths .

• Let's first create a path list , This list will store the current path we have taken
• then , We start from the root DFS, And when traversing the graph, we attach the different roots we get .
• We use it to view a node in DFS The parameter of whether to jump safely in is ：

      If there is no node in the path that we have passed .

      If we find a Hamiltonian loop , Then we don't need to traverse anymore .

Four 、 Reference code  

#------------------------------------------
'''
Defining our safe vertex as
something which is not in our
path
'''
def safeVertex(node):
if(node in path):
return False
return True
#-------------------------------------------
#-------------------------------------------
'''
Defining our DFS and
Backtracking Logic
'''
def cycleDetection(E,n,root):
path.append(root)
#Seeing all the neigbours of the current root
for i in E[root]:
#Checking if our vertex satisfies the safe Vertex
if(safeVertex(i)):
#Checking if a cycle has already been detected or not in the
#---------------------previous recursion--------------------
if(cycleDetection(E,n,i)):
return True
#Checking if our current path has all the vertices
if(len(path) == n):
#If there is an edge from last vertex to the first vertex in our path
#-------------then we have an hamiltonian cycle---------------------
if(path[0] in E[path[len(path)-1]]):
return True
else:
return False
#once we are done we remove that particle from the iteration
path.pop()
#-------------------------------------------
#-------------------------------------------
'''
Printing True or False
based on our output from Cycle Detection
'''
def HamiltonianCycle(E,n,root):
if(cycleDetection(E,n,root)):
print("True")
else:
print("False")
#-------------------------------------------
path = []
N_Vertices = int(input())
matrix = list()
for i in range(N_Vertices):
matrix.append([])
N_Edges = int(input())
for j in range(N_Edges):
edge_vertices = input().split()
u = int(edge_vertices[0])
v = int(edge_vertices[1])
matrix[u-1].append(v-1)
matrix[v-1].append(u-1)
HamiltonianCycle(matrix,N_Vertices,0)
#This path is actually a Hamiltonian cycle.
print(path)