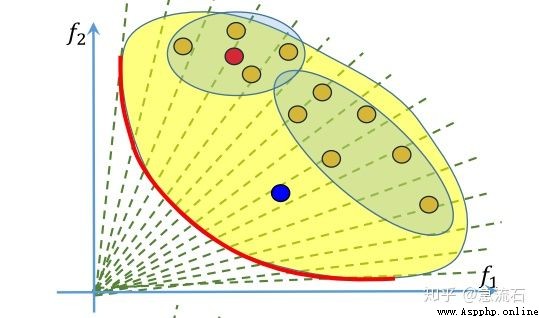
answer : Each solution corresponds to a set of weights , That is, the sub problem , Four dots near the red dot , That is, how can its neighbors be sure ? Determined by weight , At the initialization stage of the algorithm, the neighbors corresponding to each weight are determined , That is, the neighbor subproblem of each subproblem . Weighted neighbors are judged by Euclidean distance . Take the nearest few .
https://blog.csdn.net/Twobox/p/16408751.html
https://www.zhihu.com/question/263555181?sort=created Two of the answers were very good
1. Input N m
# N Indicates the point density m Represents the problem dimension
1.1 Input T
# Means to take the nearest T As neighbors
2. Generate uniformly distributed weight vector
2.1 Calculate the Euler distance between each weight vector
3. The number of weight vectors is : Number of initial population
4. Initial population , Each individual corresponds to the weight one by one
4.1 More weighted distance , Take before T As neighbors person
5. EP = empty
# Maintain the best frontier
6. Calculate the initial global optimum Z
# Bring each into f1 f2 in , Minimum value z1 z2
7. Start the cycle N generation
7.1 For each individual , Select... In the field 2 Individuals cross mutate , get 2 A new individual
7.1.1 Update global solution z
7.2 Select randomly in the field 2 Individuals , Compare the new with the old
# The new individual brings in the sub goal problem , Direct comparison value is enough
7.3 If it's better , Replace the old individual dna
7.4 to update EP
# If there is a new solution not received , Combine the new solution with EP Compare each one , Delete the , If the new solution is not dominated by the old solution , Then join in EP
Code implementation design
# analysis
Data structures to be maintained :
The most recent T Neighbors : Consider using an object list
Uniformly distributed weight vector : A two-dimensional ndarray The array can be
The weight vector corresponds to the individual : Individual objects , Directly save the weight vector array
Distance matrix between weight vectors : Start initialization , constant
EP list, The individual inside is the reference of the object
z list
Set of objective functions ,F list domain list
# Interface design
class Person
attribute:
dns: A one-dimensional ndarray
weight\_vector: A one-dimensional ndarray
neighbor: list
o\_func:Objective\_Function Objective function
function:
mutation
cross\_get\_two\_new\_dna: return 2 Duan Xin dna
compare# Compare with the offspring
accept\_new\_dna
choice\_two\_person:p1,p2
class Moead\_Util
attribute:
N
M
T:
o\_func:Objective\_Function
pm: Mutation probability
EP:[dna1,dna2,..]
weight\_vectors: Two dimensional array
Euler\_distance: Two dimensional array
pip\_size
Z:[] # The elements here are one-dimensional ndarray Array , namely dna, Immediate solution
function:
init\_mean\_vector: Two dimensional array
init\_Euler\_distance: Two dimensional array
init\_population:[]
init\_Z: One dimensional genus pig
update\_ep
update\_Z
class Objective\_Function:
attribute:
F:[]
domain:[[0,1],[],[]]
function:
get\_one\_function:Objective\_Function
1 import numpy as np
2
3
4 class Person:
5 def \_\_init\_\_(self, dna):
6 self.dna = dna
7 self.weight\_vector = None
8 self.neighbor = None
9 self.o\_func = None # Objective function
10
11 self.dns\_len = len(dna)
12
13 def set\_info(self, weight\_vector, neighbor, o\_func):
14 self.weight\_vector = weight\_vector
15 self.neighbor = neighbor
16 self.o\_func = o\_func# Objective function
17
18 def mutation\_dna(self, one\_dna):
19 i = np.random.randint(0, self.dns\_len)
20 low = self.o\_func.domain[i][0]
21 high = self.o\_func.domain[i][1]
22 new\_v = np.random.rand() * (high - low) + low
23 one\_dna[i] = new\_v
24 return one\_dna
25
26 def mutation(self):
27 i = np.random.randint(0, self.dns\_len)
28 low = self.o\_func.domain[i][0]
29 high = self.o\_func.domain[i][1]
30 new\_v = np.random.rand() * (high - low) + low
31 self.dna[i] = new\_v
32
33 @staticmethod
34 def cross\_get\_two\_new\_dna(p1, p2):
35 # A single point of intersection
36 cut\_i = np.random.randint(1, p1.dns\_len - 1)
37 dna1 = p1.dna.copy()
38 dna2 = p2.dna.copy()
39 temp = dna1[cut\_i:].copy()
40 dna1[cut\_i:] = dna2[cut\_i:]
41 dna2[cut\_i:] = temp
42 return dna1, dna2
43
44 def compare(self, son\_dna):
45 F = self.o\_func.f\_funcs
46 f\_x\_son\_dna = []
47 f\_x\_self = []
48 for f in F:
49 f\_x\_son\_dna.append(f(son\_dna))
50 f\_x\_self.append(f(self.dna))
51 fit\_son\_dna = np.array(f\_x\_son\_dna) * self.weight\_vector
52 fit\_self = np.array(f\_x\_self) * self.weight\_vector
53 return fit\_son\_dna.sum() - fit\_self.sum()
54
55 def accept\_new\_dna(self, new\_dna):
56 self.dna = new\_dna
57
58 def choice\_two\_person(self):
59 neighbor = self.neighbor
60 neighbor\_len = len(neighbor)
61 idx = np.random.randint(0, neighbor\_len, size=2)
62 p1 = self.neighbor[idx[0]]
63 p2 = self.neighbor[idx[1]]
64 return p1, p2
1 from collections import defaultdict
2
3 import numpy as np
4
5
6 def zdt4\_f1(x\_list):
7 return x\_list[0]
8
9
10 def zdt4\_gx(x\_list):
11 sum = 1 + 10 * (10 - 1)
12 for i in range(1, 10):
13 sum += x\_list[i] ** 2 - 10 * np.cos(4 * np.pi * x\_list[i])
14 return sum
15
16
17 def zdt4\_f2(x\_list):
18 gx\_ans = zdt4\_gx(x\_list)
19 if x\_list[0] < 0:
20 print("????: x\_list[0] < 0:", x\_list[0])
21 if gx\_ans < 0:
22 print("gx\_ans < 0", gx\_ans)
23 if (x\_list[0] / gx\_ans) <= 0:
24 print("x\_list[0] / gx\_ans<0:", x\_list[0] / gx\_ans)
25
26 ans = 1 - np.sqrt(x\_list[0] / gx\_ans)
27 return ans
28
29 def zdt3\_f1(x):
30 return x[0]
31
32
33 def zdt3\_gx(x):
34 if x[:].sum() < 0:
35 print(x[1:].sum(), x[1:])
36 ans = 1 + 9 / 29 * x[1:].sum()
37 return ans
38
39
40 def zdt3\_f2(x):
41 g = zdt3\_gx(x)
42 ans = 1 - np.sqrt(x[0] / g) - (x[0] / g) * np.sin(10 * np.pi * x[0])
43 return ans
44
45
46 class Objective\_Function:
47 function\_dic = defaultdict(lambda: None)
48
49 def \_\_init\_\_(self, f\_funcs, domain):
50 self.f\_funcs = f\_funcs
51 self.domain = domain
52
53 @staticmethod
54 def get\_one\_function(name):
55 if Objective\_Function.function\_dic[name] is not None:
56 return Objective\_Function.function\_dic[name]
57
58 if name == "zdt4":
59 f\_funcs = [zdt4\_f1, zdt4\_f2]
60 domain = [[0, 1]]
61 for i in range(9):
62 domain.append([-5, 5])
63 Objective\_Function.function\_dic[name] = Objective\_Function(f\_funcs, domain)
64 return Objective\_Function.function\_dic[name]
65
66 if name == "zdt3":
67 f\_funcs = [zdt3\_f1, zdt3\_f2]
68 domain = [[0, 1] for i in range(30)]
69 Objective\_Function.function\_dic[name] = Objective\_Function(f\_funcs, domain)
70 return Objective\_Function.function\_dic[name]
1 import numpy as np
2
3 from GA.MOEAD.Person import Person
4
5
6 def distribution\_number(sum, m):
7 # take m Number , The sum of numbers is N
8 if m == 1:
9 return [[sum]]
10 vectors = []
11 for i in range(1, sum - (m - 1) + 1):
12 right\_vec = distribution\_number(sum - i, m - 1)
13 a = [i]
14 for item in right\_vec:
15 vectors.append(a + item)
16 return vectors
17
18
19 class Moead\_Util:
20 def \_\_init\_\_(self, N, m, T, o\_func, pm):
21 self.N = N
22 self.m = m
23 self.T = T # Neighbor size limit
24 self.o\_func = o\_func
25 self.pm = pm # Mutation probability
26
27 self.Z = np.zeros(shape=m)
28
29 self.EP = [] # the front
30 self.EP\_fx = [] # ep The corresponding target value
31 self.weight\_vectors = None # Uniform weight vector
32 self.Euler\_distance = None # Euler distance matrix
33 self.pip\_size = -1
34
35 self.pop = None
36 # self.pop\_dna = None
37
38 def init\_mean\_vector(self):
39 vectors = distribution\_number(self.N + self.m, self.m)
40 vectors = (np.array(vectors) - 1) / self.N
41 self.weight\_vectors = vectors
42 self.pip\_size = len(vectors)
43 return vectors
44
45 def init\_Euler\_distance(self):
46 vectors = self.weight\_vectors
47 v\_len = len(vectors)
48
49 Euler\_distance = np.zeros((v\_len, v\_len))
50 for i in range(v\_len):
51 for j in range(v\_len):
52 distance = ((vectors[i] - vectors[j]) ** 2).sum()
53 Euler\_distance[i][j] = distance
54
55 self.Euler\_distance = Euler\_distance
56 return Euler\_distance
57
58 def init\_population(self):
59 pop\_size = self.pip\_size
60 dna\_len = len(self.o\_func.domain)
61 pop = []
62 pop\_dna = np.random.random(size=(pop\_size, dna\_len))
63 # Of the original individual dna
64 for i in range(pop\_size):
65 pop.append(Person(pop\_dna[i]))
66
67 # Of the original individual weight\_vector, neighbor, o\_func
68 for i in range(pop\_size):
69 # weight\_vector, neighbor, o\_func
70 person = pop[i]
71 distance = self.Euler\_distance[i]
72 sort\_arg = np.argsort(distance)
73 weight\_vector = self.weight\_vectors[i]
74 # neighbor = pop[sort\_arg][:self.T]
75 neighbor = []
76 for i in range(self.T):
77 neighbor.append(pop[sort\_arg[i]])
78
79 o\_func = self.o\_func
80 person.set\_info(weight\_vector, neighbor, o\_func)
81 self.pop = pop
82 # self.pop\_dna = pop\_dna
83
84 return pop
85
86 def init\_Z(self):
87 Z = np.full(shape=self.m, fill\_value=float("inf"))
88 for person in self.pop:
89 for i in range(len(self.o\_func.f\_funcs)):
90 f = self.o\_func.f\_funcs[i]
91 # f\_x\_i: An individual , In the i Value on target
92 f\_x\_i = f(person.dna)
93 if f\_x\_i < Z[i]:
94 Z[i] = f\_x\_i
95
96 self.Z = Z
97
98 def get\_fx(self, dna):
99 fx = []
100 for f in self.o\_func.f\_funcs:
101 fx.append(f(dna))
102 return fx
103
104 def update\_ep(self, new\_dna):
105 # Combine the new solution with EP Compare each one , Delete the
106 # If the new solution is not dominated by the old solution , The retention
107 new\_dna\_fx = self.get\_fx(new\_dna)
108 accept\_new = True # Whether to add the new solution to EP
109 # print(f" Ready to start the cycle : EP length {len(self.EP)}")
110 for i in range(len(self.EP) - 1, -1, -1): # Go back and forth
111 old\_ep\_item = self.EP[i]
112 old\_fx = self.EP\_fx[i]
113 # old\_fx = self.get\_fx(old\_ep\_item)
114 a\_b = True # The old ruling line
115 b\_a = True # The new rules the old
116 for j in range(len(self.o\_func.f\_funcs)):
117 if old\_fx[j] < new\_dna\_fx[j]:
118 b\_a = False
119 if old\_fx[j] > new\_dna\_fx[j]:
120 a\_b = False
121 # T T : fx equal Do not change directly EP
122 # T F : The old rules the new Stay old , Never new , End of cycle .
123 # F T : The new rules the old Stay new , Don't be so old , Continue to cycle
124 # F F : Non dominant relationship Do not operate , Cycle to the next
125 # TF Why end the loop ,FT Why continue the cycle , You can think about
126 if a\_b:
127 accept\_new = False
128 break
129 if not a\_b and b\_a:
130 if len(self.EP) <= i:
131 print(len(self.EP), i)
132 del self.EP[i]
133 del self.EP\_fx[i]
134 continue
135
136 if accept\_new:
137 self.EP.append(new\_dna)
138 self.EP\_fx.append(new\_dna\_fx)
139 return self.EP, self.EP\_fx
140
141 def update\_Z(self, new\_dna):
142 new\_dna\_fx = self.get\_fx(new\_dna)
143 Z = self.Z
144 for i in range(len(self.o\_func.f\_funcs)):
145 if new\_dna\_fx[i] < Z[i]:
146 Z[i] = new\_dna\_fx[i]
147 return Z
import random
import numpy as np
from GA.MOEAD.Moead\_Util import Moead\_Util
from GA.MOEAD.Objective\_Function import Objective\_Function
from GA.MOEAD.Person import Person
import matplotlib.pyplot as plt
def draw(x, y):
plt.scatter(x, y, s=10, c="grey") # s Size of points c The color of the point alpha transparency
plt.show()
iterations = 1000 # The number of iterations
N = 400
m = 2
T = 5
o\_func = Objective\_Function.get\_one\_function("zdt4")
pm = 0.7
moead = Moead\_Util(N, m, T, o\_func, pm)
moead.init\_mean\_vector()
moead.init\_Euler\_distance()
pop = moead.init\_population()
moead.init\_Z()
for i in range(iterations):
print(i, len(moead.EP))
for person in pop:
p1, p2 = person.choice\_two\_person()
d1, d2 = Person.cross\_get\_two\_new\_dna(p1, p2)
if np.random.rand() < pm:
p1.mutation\_dna(d1)
if np.random.rand() < pm:
p1.mutation\_dna(d2)
moead.update\_Z(d1)
moead.update\_Z(d2)
t1, t2 = person.choice\_two\_person()
if t1.compare(d1) < 0:
t1.accept\_new\_dna(d1)
moead.update\_ep(d1)
if t2.compare(d1) < 0:
t2.accept\_new\_dna(d2)
moead.update\_ep(d1)
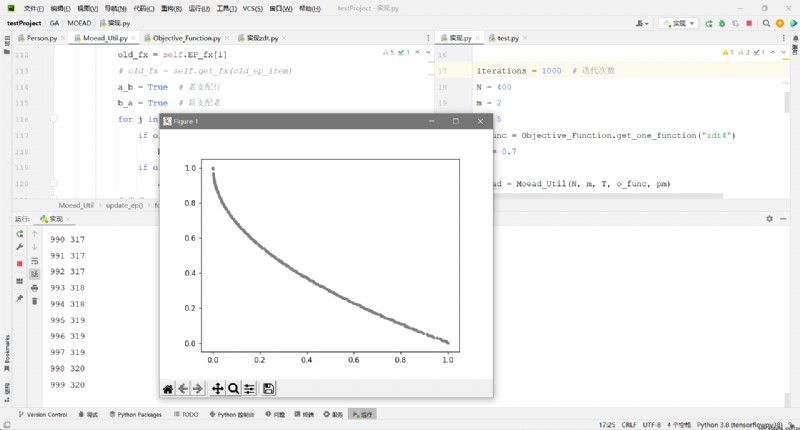
# Output result drawing
EP\_fx = np.array(moead.EP\_fx)
x = EP\_fx[:, 0]
y = EP\_fx[:, 1]
draw(x, y)