一、哈密頓問題的歷史

        哈密頓路徑問題在上世紀七十年代初，終於被證明是“NP完全”的。據說具有這樣性質的問題，難於找到一個有效的算法。實際上對於某些頂點數不到100的網絡，利用現有最好的算法和計算機也需要比較荒唐的時間（比如幾百年）才能確定其是否存在一條這樣的路徑。

二、哈密頓循環在圖論的定義

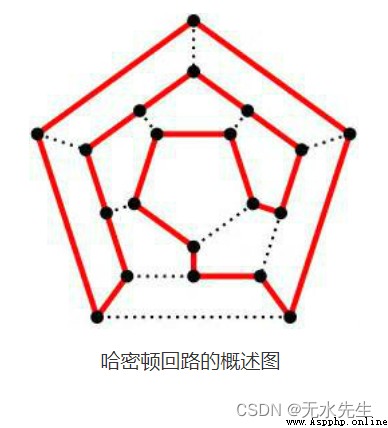
        哈密頓回路的定義： G=(V,E)是一個圖，若G中一條路徑通過且僅通過每一個頂點一次，稱這條路徑為哈密頓路徑。若G中一個回路通過且僅通過每一個頂點一次，稱這個環為哈密頓回路。若一個圖存在哈密頓回路，就稱為哈密頓圖。

三、深度優先遍歷（Depth First Search, 簡稱 DFS）

        深度優先遍歷主要思路是從圖中一個未訪問的頂點 V 開始，沿著一條路一直走到底，然後從這條路盡頭的節點回退到上一個節點，再從另一條路開始走到底…，不斷遞歸重復此過程，直到所有的頂點都遍歷完成，它的特點是不撞南牆不回頭，先走完一條路，再換一條路繼續走。

        為了找到哈密頓循環，我們將使用回溯和 DFS 來遍歷所有可能的不同類型的哈密頓路徑。

• 我們首先創建一個路徑列表，該列表將存儲我們走過的當前路徑
• 然後，我們從根開始一個 DFS，並在遍歷圖時不斷附加我們得到的不同根。
• 我們用來查看一個節點在 DFS 中是否可以安全跳轉的參數是：

     如果我們已經走過的路徑中不存在節點。

     如果我們找到了一個哈密頓循環，那麼我們就不需要再遍歷了。

四、參考代碼 

#------------------------------------------
'''
Defining our safe vertex as
something which is not in our
path
'''
def safeVertex(node):
if(node in path):
return False
return True
#-------------------------------------------
#-------------------------------------------
'''
Defining our DFS and
Backtracking Logic
'''
def cycleDetection(E,n,root):
path.append(root)
#Seeing all the neigbours of the current root
for i in E[root]:
#Checking if our vertex satisfies the safe Vertex
if(safeVertex(i)):
#Checking if a cycle has already been detected or not in the
#---------------------previous recursion--------------------
if(cycleDetection(E,n,i)):
return True
#Checking if our current path has all the vertices
if(len(path) == n):
#If there is an edge from last vertex to the first vertex in our path
#-------------then we have an hamiltonian cycle---------------------
if(path[0] in E[path[len(path)-1]]):
return True
else:
return False
#once we are done we remove that particle from the iteration
path.pop()
#-------------------------------------------
#-------------------------------------------
'''
Printing True or False
based on our output from Cycle Detection
'''
def HamiltonianCycle(E,n,root):
if(cycleDetection(E,n,root)):
print("True")
else:
print("False")
#-------------------------------------------
path = []
N_Vertices = int(input())
matrix = list()
for i in range(N_Vertices):
matrix.append([])
N_Edges = int(input())
for j in range(N_Edges):
edge_vertices = input().split()
u = int(edge_vertices[0])
v = int(edge_vertices[1])
matrix[u-1].append(v-1)
matrix[v-1].append(u-1)
HamiltonianCycle(matrix,N_Vertices,0)
#This path is actually a Hamiltonian cycle.
print(path)