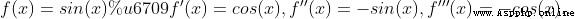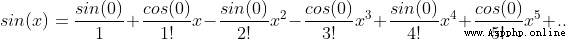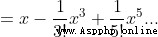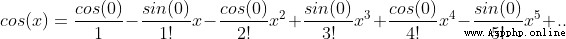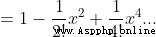本文內容來自於學習麻省理工學院公開課：單變量微積分-泰勒級數-網易公開課

Bullseye：第一單元 用python學習微積分（一） 安裝開發環境Anaconda 和 導數（上）- 1/x的導數

質心問題Center of Mass - Sciencetopia

重心問題Center of Gravity Definition, Equation and Calculation

Bullseye：第一單元 用python學習微積分（二）VSCode 、PYGame 和 導數（上）- 瞬時速度

目錄

一、重心和質心

1、質心

（1）一個物體

（2）系統質心：

2、重心

（1）單一物體

（2）系統重心：

3、不同形狀的重心位置

二、重心問題

1、實驗

2、用級數的想法來考慮這個問題,老師的思想實驗

（1）設置

（2）計算

（3）計算跨越26個單位長度距離需要多少木塊堆積？

（4）老師要求注意，盡管這個級數是沒有極限的，但是這個級數的增長十分的緩慢。

三、冪級數

1、幾何級數 （Geomeric Series）

（1）證明

2、冪級數的一般形式

（1）公式

（2）如何判斷

3、收斂冪級數的法則（和多項式類似）

4、泰勒公式（Taylor's Formula）

5、泰勒公式的應用（ 求取 e ）

6、求取sin(x)

7、求取cos(x)

一、重心和質心

1、質心

（1）一個物體

剛體由大量粒子組成，剛體的質量是單個粒子質量的總和。但是，我們可以考慮物體上的一個點，使得物體的全部質量都集中在它上面，並且當施加相同的力時，該點的運動與與物體質量相同的粒子的運動相同.這個點稱為質心。因此，物體的質心是施加的力產生線性加速度但沒有旋轉的點。

單個物體上的受力是由其上面每個粒子所受力的總和

​

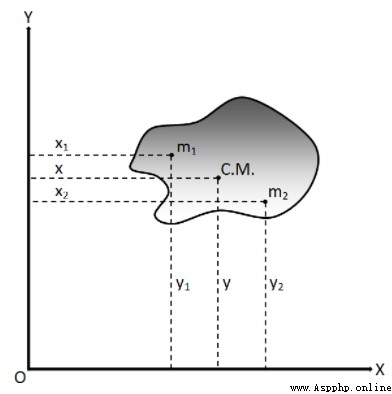
設置：如圖總質量為M；質心為C.M.； 'm1, m2 ...' 為物體上某點的質量

質心公式（center of mass [x, y]）=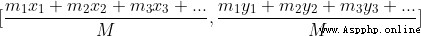

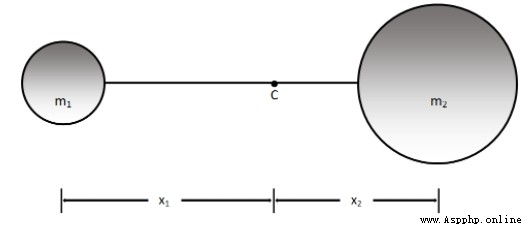
（2）系統質心：

​

設置： 兩個質量為m1和m2的物體，如圖所示。讓質量通過剛性桿連接，並讓C是它們的質心。

有公式：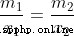

2、重心

重心是物體的重量作用並且物體上的總重力扭矩為零的點，簡寫C.G.

（1）單一物體

​

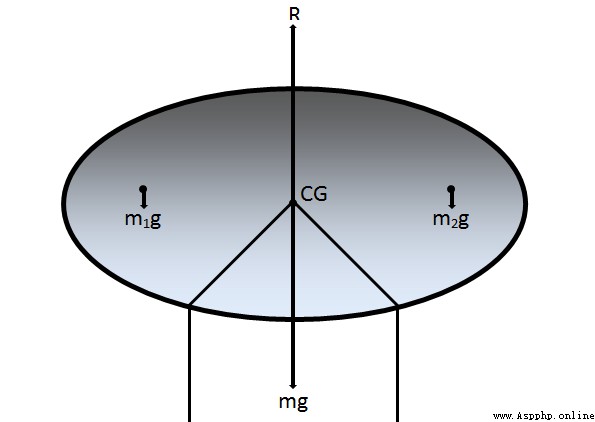
設置：物體上某粒子的重力 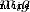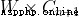， 是這個粒子從紙板的 CG 的位置向量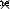， 是這個粒子上重力的扭矩

我們知道在CG點總重力扭矩是 0，所以有

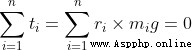
由於 g 是常數，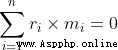

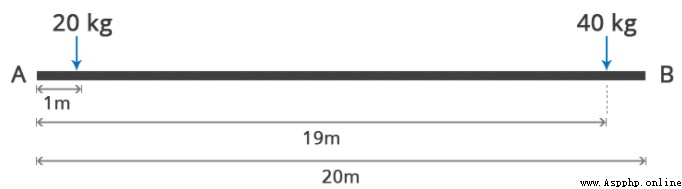
（2）系統重心：

設置：兩個寬2m的鐵塊 a, b，分別重20kg，40kg，並分別放置在木板兩側A、B，木板長20m。

​

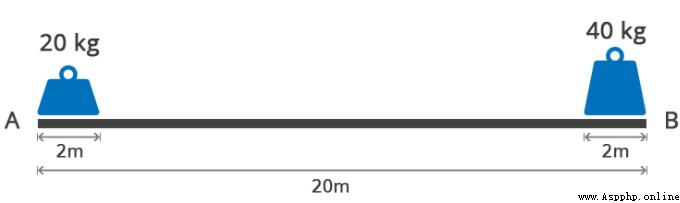
a 的重心距離 A 點1m，而 b 的重心距離A點19m

​

以左側A點為基准

系統重心 = 總重力扭矩 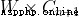總的力臂 = （A的力臂 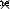A點受力 + B的力臂 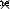B點受力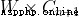） （A點受力 + B點力臂）

總重力扭矩=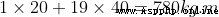

系統重心距離左側=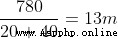

3、不同形狀的重心位置

體型

CG位置

細均勻條

條的中點

圓環

環的中心

圓盤

磁盤中心

球體、空心球體、環形盤

在它的中心

立方體或矩形塊

對角線的交點

三角板

中線的交點

方形層、平行四邊形和矩形層

對角線的交點

圓柱

軸的中點

圓錐或金字塔

在與底面中心頂點相接的線上，距底面的距離等於該線長度的1/4

二、重心問題

​

如圖，有多個積木搭在一起，由下向上，每塊都向左偏移一定的距離，問最上面那一塊的右測可不可以偏移到最下面的積木的左測以左。

1、實驗

老師用幾塊積木做了這個實驗，並且成功了。這裡的秘密就是要從上向下布置。

其原理是，由於只要在積木的重心處有支撐，積木就可以立住。

第一塊積木的重心在他的中心位置，所以第二塊積木要放在第一塊的一半處（積木都是等大小的，所以我們只需要考慮水平方向的位置，xCenter1）。第一塊和第二塊積木形成了新的系統，這個系統的重心在原第一塊和第二塊重心的平均的位置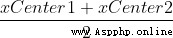（ ）, 以此類推當有n個積木以此方法布置時，它們組成的系統的重心為( )

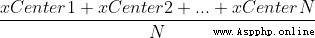模擬程序：

​

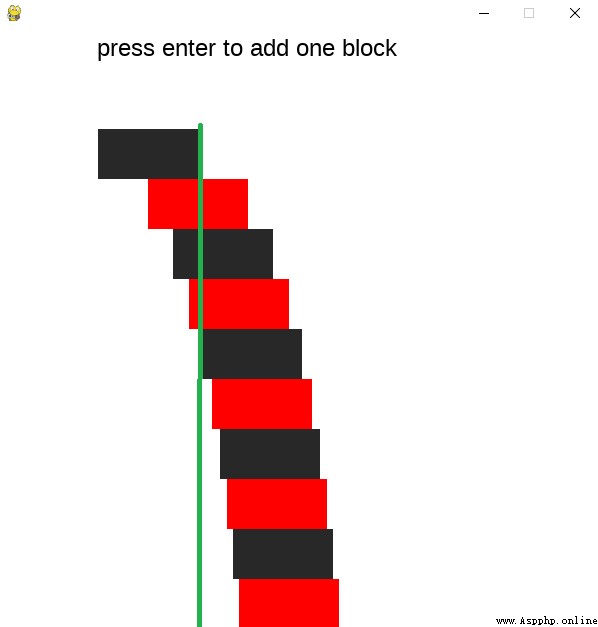
pygame基礎上制作的模擬程序

鏈接：百度網盤 請輸入提取碼

提取碼：1g1u

解壓7z，並在解壓目錄中運行 AddRectangles.py。 程序中點擊鍵盤回車可以添加一個積木。

2、用級數的想法來考慮這個問題,老師的思想實驗

（1）設置：積木長 L = 2，重力 W = 1 ，位置因素只考慮x方向變化，使用貪婪算法，從上向下布置，第n+1塊積木所在的位置是：第n塊積木的重心和第n+1塊積木重心的平均數，也就是   和 的平均數。由於每塊積木的重量相等，則第n塊積木累積了n的重量，而n+1塊積木有重量 1，它們的平均值是

​

（2）計算

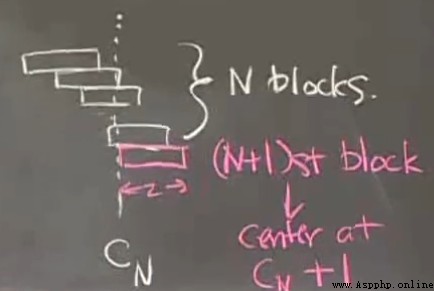
考慮重心中系統重心的公式

以原點計，

系統重心 = 總重力扭矩 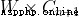 總的力臂 = （A的力臂  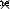A點受力 + B的力臂  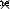B點受力）  （A點受力 + B點力臂）

也就是第n+1塊積木的左側是在前n塊積木的重心 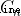（W=1，重力為 n ） 下方，也就是說第n+1塊積木的重心在 （ 重力為 1 ）

再把重量考慮進去，則這個新的重心在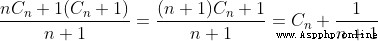

程序：

import numpy as np
from sympy import *
import matplotlib.pyplot as plt
def GetCenter(steps, weight, length):
Cn = 0
for i in range(steps):
n = i
Cn = (Cn*weight*n + (Cn + length/2.0)*weight)/(n+1)
print(Cn)
W = 1
L = 2
GetCenter(100,weight=W,length =L)
1.0
1.5
1.8333333333333333
2.083333333333333
2.2833333333333328
...
5.177377517639616
5.187377517639615

按公式展開：

....

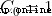
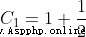
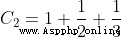
由上一章得知：

Bullseye：第五單元 用python學習微積分（三十三）反常積分（下）-- 無窮級數和收斂判定

黎曼上和（ ）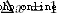

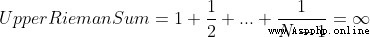
顯然這個 （ 發散的 ）

（3）計算跨越26個單位長度距離需要多少木塊堆積？

由上一章的知識可知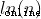，   近似並小於 （ ）,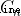

這裡要注意，每個木塊被定義為2個單位距離，所以當我們需要跨越26個單位距離時，

首先要減掉最下面那塊的2個單位距離，然後就是其余的積木的重心到目標位置的距離即24個單位距離，也就是 ， 由於 ，也就是讓第24個單位距離處為這n塊積木的重心，求 n+1（顯然 n 是整數）。

x = symbols('x')
eq = ln(x)-24
eq1 = Eq(eq,0)
solveX = solve(eq1)
print(int(solveX[0]))
26489122129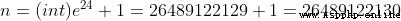

假設木塊高3cm，這些木塊摞起來有多高呢 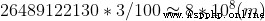？ ，大約等於地球到月亮的距離的2倍

（4）老師要求注意，盡管這個級數是沒有極限的，但是這個級數的增長十分的緩慢。

三、冪級數

1、幾何級數 （Geomeric Series）

當 |x| < 1

（1）證明

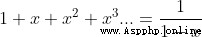
假設有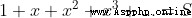

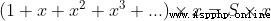
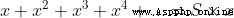
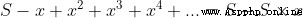
由於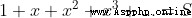

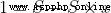
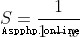
這個證明要求S首先要存在，也就是這個冪級數要是收斂的，不能是發散的。

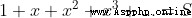當 時，等式 會變成,造成結果無意義。

2、冪級數的一般形式

（1）公式

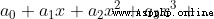
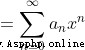
(收斂半徑 radius of converges)

（級數收斂點集區間）

當 R" class=mathcode src="//img.inotgo.com/imagesLocal/202206/28/202206280438092099_19.gif"> 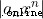， 是發散的

當 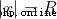, 是邊界，並不會被使用

（2）如何判斷

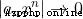以指數速度趨向0 ，當

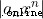不會趨向0 ，當R" class=mathcode src="//img.inotgo.com/imagesLocal/202206/28/202206280438092099_19.gif">

3、收斂冪級數的法則（和多項式類似）

這些運算對冪級數來說都是成立的

（1）運算舉例

4、泰勒公式（Taylor's Formula）

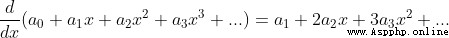
注意：使用泰勒公式時，當 n=0 時， 約定俗成 0! = 1

泰勒公式的本質是近似，當 f(x)在 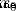處有n階導數，則有這個函數可以用冪函數近似替代，有公式

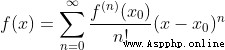
當這個函數在 x=0 處有n階導數，泰勒公式變換為更常用的麥克勞林公式

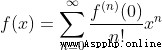
當這個展開式n值越大，近似度就越高

通常在冪級數中，

證明：

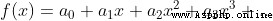
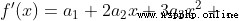
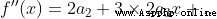
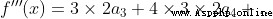
x 取 0，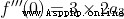

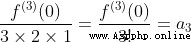
5、泰勒公式的應用（ 求取 e ）

我們知道，當 ,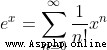

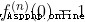
所以我們可以把它帶入泰勒公式，有

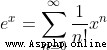
而

6、求取sin(x)

我們知道，當

7、求取cos(x)