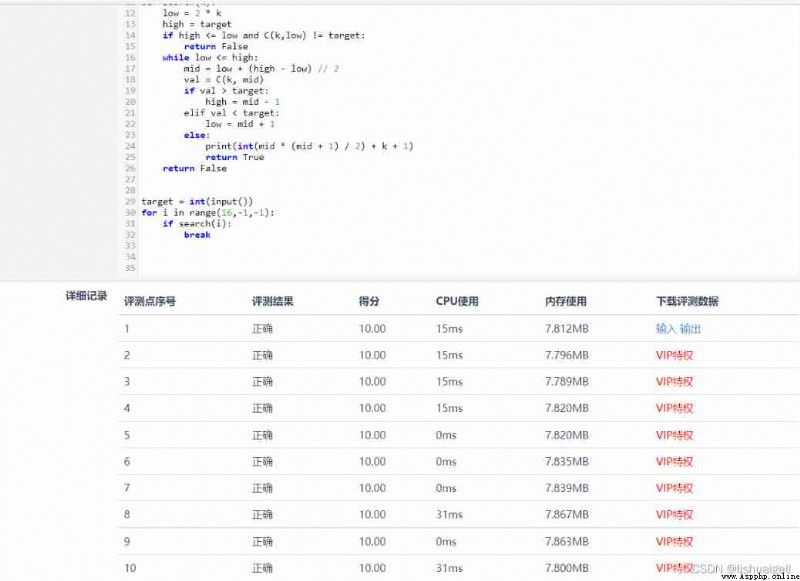
If you still don't understand, hit me at last ~
When we see Yanghui triangle, it is easy to think that the value of a number is equal to the sum of two numbers on its shoulders . So , The number of the next row can be calculated from the number of the previous row , Repeat the above operation , Until we find the target . But after looking at the scale of the use case, I found that it involves the power of ten to the nineth , The number is very large , Only 20% Use cases for 10 within , If you solve it by enumerating just now, the score is not high . So we can see that , This is a thinking problem , We need to find out the law to solve .
Let's look for the rules , It can be found that Yanghui triangle has the following characteristics :
1. symmetry
The numbers on the left and right sides of Yang Hui triangle are symmetrical and equal .
2. Incremental
The bigger the number in the middle , Except the outermost layer 1 Outside , The lower the number, the bigger the number .
3. Combinatorial number
Every element in Yang Hui triangle can be represented by combinatorial number . The first N OK, No M Columns can be expressed as C(N-1,M-1), Such as 6 In the 5 OK, No 3 Column , Its corresponding combination number is C(5-1,3-1), namely C(4,2).
Because to find out the first time N Position of appearance , According to the symmetry ,N It must appear on the left , Therefore, only the position of the left half can be considered . Because the number in the middle is bigger , So we can count from the middle , That is, starting from the number of positions of the axis of symmetry . How to find it ? Look sideways for . you 're right , Just look sideways .
Let's remove the right half of the triangle , Then separate each diagonal line .
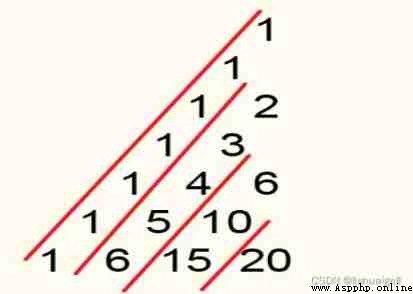
Why do you look sideways ?
Because the closer you get to the inner diagonal, the greater the value of each element , And it always comes first . Pictured above is an example ,6 In the penultimate oblique line appears , His corresponding position is No 5 Xing di 3 Column , Also in the penultimate oblique line , The right position is No 7 Xing di 2 Column . Obviously , The penultimate oblique 6 Is obviously behind the former . The reason for this is that the growth rate of each oblique line is different , The closer to the expert, the faster the value increases . For example , Finish the same problem , Expert 15 It'll be done in minutes , The layman may spend 1 Hours .
Why can I look sideways ?
Because they are regular : The position of the column corresponding to the element of each oblique row has not changed . Or to 6 For example ,6 In the 3 Column ,6 The next element of the diagonal line 10 Also in the third column .(6:C(4, 2), 10:C(5, 2)). Finally, when we find the element, we can deduce the position of the element in the whole Yanghui triangle according to the law of combination number .
After solving the above doubts , It's time to think about how to look sideways . Before thinking , Let's first look at what the downward slope is nature .
How to look sideways ?
Because the elements always appear first in the inner oblique line , So we're going to start with an inward slope From inside out Start looking for , Find No 0 All right 1 Up to the outermost layer of . To what extent can we ? Inside to the 16 That's ok . We know that the elements on the central axis of symmetry are the smallest in every oblique row , It is characterized by C( k, 2k ) .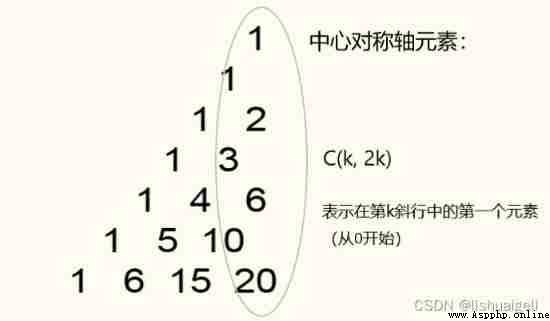
If the skew minimum elements have exceeded 10 Of 9 Power, then the remaining elements are greater than 10 Of 9 Subordinate , In other words, this oblique line is meaningless , Don't have to consider . Calculated , Only 16 The number within the diagonal line meets the condition .
We have identified the starting element , According to the increasing nature of Yang Hui triangle , The lower the element, the greater the value , The explanation is orderly , have access to Two points search Improve search efficiency . Here is a template for binary search and sorting , You can refer to my This article .
After determining the start position of the search, you should determine the end position of the search . We take the target value as the lower limit of our combinatorial number . go back to analysis The third dot in : The lower limit of the combination number indicates the number of rows in which the element is located -1, Then if the target value is taken as the lower limit of the number of combinations at the end position, it is already very large , Even if you can't find it, there is a third 1 Oblique travel ( All for 1 Yes, it is 0 Oblique travel ) The tolerance of is 1 The arithmetical sequence of , So I'm sure I can find .
Because the upper limit of the number of combinations of the same oblique line remains unchanged , We constantly change the value of the lower limit of the combination number , Until the target value is finally found . Find the target value , According to the upper and lower bounds of the combination number at this time , The position of the element can be obtained by combining the property of Yanghui triangle combination number . With 20: C( 6, 3 ) For example , It is , The first 7 Xing di 4 Elements . front 6 The line is a tolerance of 1 Equal difference sequence of , According to the summation formula, we can find 6 There are several elements in a row , Finally, add 4 That is to say 20 The position of .
Precision problem : Because the last output is an integer , So finally use int Remove the number after the decimal point in the calculation result . Suppose an element is found after hundreds of thousands of rows , Then ask for his position before N The sum of terms is very large , But the number of columns he is in may be very small , If you add them up and convert them to integers, you will lose data , The result is inconsistent with the actual result . If you put it on the Blue Bridge Cup, you can only get 80 points . The hard-working problem can not get full marks because of the accuracy problem , It's true, but it's a pity . I've been thinking about this problem for a long time and haven't found the root of the problem , Finally, I saw an article that woke me up , thank @Py Xiao Zheng .
# Find the combination number
def C(a, b): # a Is the upper limit , b Is the lower limit
res = 1
for i in range(a):
res *= b / a
# When the result is greater than the target value, there is no need to continue the operation , Increase of efficiency
if res > target:
return res
b -= 1
a -= 1
return res
# Binary search target element
def search(k):
# Starting lower limit , That is, the element of the position of the axis of symmetry
low = 2 * k
# Lower end point
high = target
# May appear high Less than low The situation of , For example, the target value is very small , But when the number of lines is still more than ten .
# At this time, directly judge whether the value of the first element of the oblique line, that is, the element at the position of the axis of symmetry, is the target value .
if high <= low and C(k, low) != target:
return False
while low <= high:
mid = low + (high - low) // 2
val = C(k, mid)
if val > target:
high = mid - 1
elif val < target:
low = mid + 1
else:
# According to the sequence of equal differences N Term and formula to find out how many elements are in front of , Then add the number of columns he is in
print(int(mid * (mid + 1) / 2) + k + 1)
return True
return False
target = int(input())
# range The second parameter must be -1, Because the first 0 Only when you walk obliquely 1.
for i in range(16, -1, -1):
if search(i):
break