如果您使用 Python 進行過任何編碼,那麼您很有可能在某個程序中使用了數字。例如,您可能使用整數來指定列表中值的索引。
但是 Python 中的數字不僅僅是它們的原始值。讓我們看看你可能不知道的關於 Python 中數字的三件事。
Python 中有個概念叫做:一切皆對象。您在 Python 中學習的第一個對象 "HelloWorld" 是表示字符串的 str 對象。
然後你學習了字符串有方法,例如 .lower() 方法,它返回一個全小寫字符的新字符串:
>>> "HELLO".lower()'hello'比如首字母大寫 capitalize(), 返回字符串的副本,其第一個字符大寫,其余小寫。
>>> mystring = "hello python">>> print(mystring.capitalize())Hello pythonPython 中的數字也是對象,就像字符串一樣,也有自己的方法。例如,您可以使用 .to_bytes()方法將整數轉換為字節字符串:
>>> n = 255>>> n.to_bytes(length=2, byteorder="big")b'\x00\xff'其中,length 參數指定了要在字符串中使用的字節數,byteorder 參數確定字節的順序。例如,將 byteorder 設置為 “big”會返回一個字節字符串,其中最重要的字節在前,而將 byteorder 設置為 "little" 則將最不重要的字節放在最前面。
>>> n.to_bytes(length=2, byteorder="little")b'\xff\x00'255 是可以表示為 8 位整數的最大整數,因此您可以在 .to_bytes() 中設置 length=1 也沒有問題:
>>> n.to_bytes(length=1, byteorder="big")b'\xff'但是,如果在 .to_bytes() 中將 length=1 設置為 256,則會收到 OverflowError 錯誤:
>>> n = 256>>> n.to_bytes(length=1, byteorder="big")Traceback (most recent call last): File "<stdin>", line 1, in <module>OverflowError: int too big to convert您可以使用 .from_bytes() 類方法將字節字符串轉換為整數:
>>> int.from_bytes(b'\x06\xc1', byteorder="big")1729類方法是從類名而不是類實例調用的,這就是在上面的 int 上調用 .from_bytes() 方法的原因。
浮點數也有方法。也許對浮點數最有用的方法是 .is_integer() ,它用於檢查浮點數是否沒有小數部分:
>>> n = 2.0>>> n.is_integer()True>>> n = 3.14>>> n.is_integer()False一種有趣的浮點方法是 .as_integer_ratio() 方法,它返回一個元組,其中包含表示浮點值的分數的分子和分母:
>>> n = 0.75>>> n.as_integer_ratio()(3, 4)但是,由於浮點表示錯誤,此方法可能會返回一些意外值:
>>> n = 0.1>>> n.as_integer_ratio()(3602879701896397, 36028797018963968)如果需要,您可以通過用括號括住文字來調用數字類型上的方法:
>>> (255).to_bytes(length=1, byteorder="big")b'\xff'>>> (3.14).is_integer()False如果你沒有用括號括起整數文字,當你調用一個方法時你會看到一個 SyntaxError ——盡管奇怪的是,你不需要帶有浮點文字的括號:
>>> 255.to_bytes(length=1, byteorder="big") File "<stdin>", line 1 255.to_bytes(length=1, byteorder="big") ^SyntaxError: invalid syntax>>> 3.14.is_integer()False您可以在文檔中找到 Python 數字類型可用方法的完整列表:
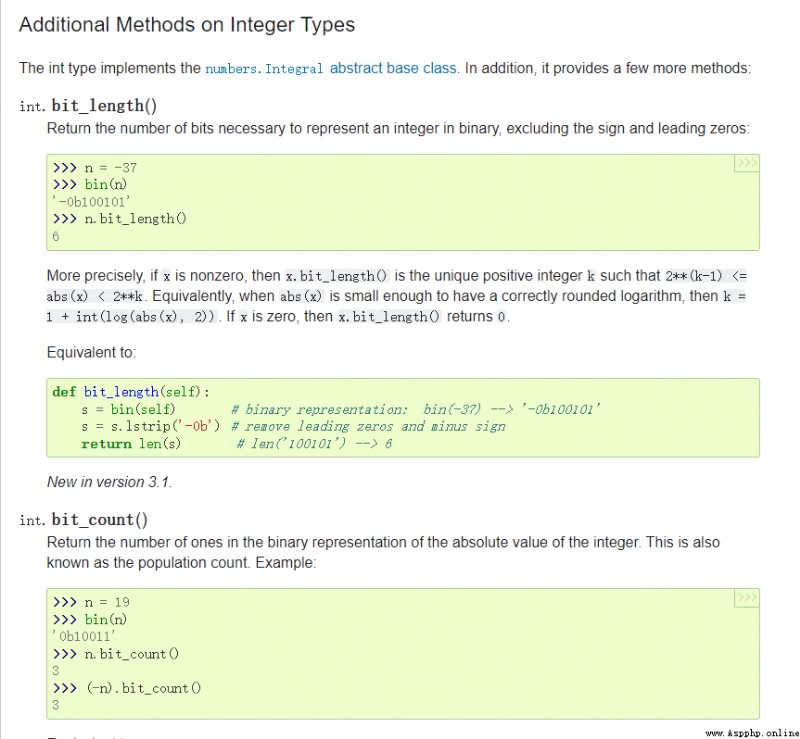
在數學中,數字具有自然的層次結構。例如,所有自然數都是整數,所有整數都是有理數,所有有理數都是實數,所有實數都是復數。
Python 中的數字也是如此。這個“數字塔”通過 numbers模塊中包含的抽象類型來表示。
Python 中的每個數字都是 Number 類的一個實例:
>>> from numbers import Number>>> # Integers inherit from Number>>> isinstance(1729, Number)True>>> # Floats inherit from Number>>> isinstance(3.14, Number)True>>> # Complex numbers inherit from Number>>> isinstance(1j, Number)True如果您需要檢查 Python 中的值是否為數字,但您不關心該值是什麼類型的數字,請使用 isinstance(value, Number)。
Python 附帶了四種額外的抽象類型,其層次結構從最通用的數字類型開始,如下所示:
Complex 類用於表示復數。有一種內置的具體 Complex 類型:complex。
Real 類用於表示實數。有一種內置的具體 Real 類型:float。
Rational 類用於表示有理數。有一種內置的具體 Rational 類型:Fraction。
Integral 類用於表示整數。有兩種內置的具體 Integral 類型:int 和 bool。
你可以在你的終端中驗證所有這些:
>>> import numbers>>> # Complex numbers inherit from Complex>>> isinstance(1j, numbers.Complex)True>>> # Complex numbers are not Real>>> isinstance(1j, numbers.Real)False>>> # Floats are Real>>> isinstance(3.14, numbers.Real)True>>> # Floats are not Rational>>> isinstance(3.14, numbers.Rational)False>>> # Fractions are Rational>>> from fractions import Fraction>>> isinstance(Fraction(1, 2), numbers.Rational)True>>> # Fractions are not Integral>>> isinstance(Fraction(1, 2), numbers.Integral)False>>> # Ints are Integral>>> isinstance(1729, numbers.Integral)True>>> # Bools are Integral>>> isinstance(True, numbers.Integral)True>>> True == 1True>>> False == 0True不過,仔細看看,有幾件事對 Python 的數字層次結構有些怪異。
Python 數字塔中的四種抽象類型對應的具體數值類型有四種:complex, float, Fraction, 和 int.
但是 Python 有第五種數字類型,即 Decimal類,用於精確表示十進制數並克服浮點運算的限制。
你可能猜到 Decimal 數是實數,但你錯了:
>>> from decimal import Decimal>>> import numbers>>> isinstance(Decimal("3.14159"), numbers.Real)False事實上,Decimal 數字繼承自的唯一類型是 Python 的 Number 類:
>>> isinstance(Decimal("3.14159"), numbers.Complex)False>>> isinstance(Decimal("3.14159"), numbers.Rational)False>>> isinstance(Decimal("3.14159"), numbers.Integral)False>>> isinstance(Decimal("3.14159"), numbers.Number)TrueDecimal 不繼承自 Integral 是有道理的。在某種程度上,Decimal 不繼承自 Rational 也是有道理的。但是為什麼 Decimal 不從 Real 或 Complex 繼承呢?
答案就在 CPython 源代碼中:
Decimal 具有 Real abc 指定的所有方法,但不應將其注冊為 Real,因為小數不與二進制浮點數互操作(例如:Decimal('3.14') + 2.71828 是不支持的)。但是,抽象實數預計可以互操作(即,如果 R1 和 R2 都是實數,則 R1 + R2 應該可以工作)。
這一切都歸結為實現。
另一方面,浮點數實現了 Real 的抽象基類,並用於表示實數。但是,由於有限的內存約束,浮點數僅僅是實數的有限近似值。這令人困惑,如以下內容:
>>> 0.1 + 0.1 + 0.1 == 0.3False浮點數作為二進制分數存儲在內存中,但這會導致一些問題。
就像分數一樣 1/3 沒有有限的十進制表示——小數點後有無數個三。
分數 1/10 沒有有限二進制分數表示。換句話說,你不能以精確的精度將 0.1 存儲在計算機上——除非那台計算機有無限的內存。
從嚴格的數學角度來看,所有浮點數都是有理數——除了 float("inf") 和 float("nan")。但是程序員使用它們來近似實數並將它們在大多數情況下視為實數。
float("nan") 是一個特殊的浮點值,表示“非數字”值——通常縮寫為 NaN 值。但是由於 float 是數字類型,所以 isinstance(float("nan"), Number) 返回 True
沒錯:“不是數字”值是數字。("not a number" values are numbers.)
這就是浮點數的奇怪之處。
Python 的抽象數字基類型允許您創建自己的自定義抽象和具體數字類型。
即利用 Python 中關於數字的類型,比如 numbers 中的類型,可以定義其他有特殊屬性和方法的數字對象。
例如,考慮下面的類 ExtendedInteger,它實現了 a+b \sqrt p 形式的數字,其中 a和 b 是整數,p 是素數(請注意,類不強制素數):
import mathimport numbersclass ExtendedInteger(numbers.Real): def __init__(self, a, b, p = 2) -> None: self.a = a self.b = b self.p = p self._val = a + (b * math.sqrt(p)) def __repr__(self): return f"{self.__class__.__name__}({self.a}, {self.b}, {self.p})" def __str__(self): return f"{self.a} + {self.b}√{self.p}" def __trunc__(self): return int(self._val) def __float__(self): return float(self._val) def __hash__(self): return hash(float(self._val)) def __floor__(self): return math.floor(self._val) def __ceil__(self): return math.ceil(self._val) def __round__(self, ndigits=None): return round(self._val, ndigits=ndigits) def __abs__(self): return abs(self._val) def __floordiv__(self, other): return self._val // other def __rfloordiv__(self, other): return other // self._val def __truediv__(self, other): return self._val / other def __rtruediv__(self, other): return other / self._val def __mod__(self, other): return self._val % other def __rmod__(self, other): return other % self._val def __lt__(self, other): return self._val < other def __le__(self, other): return self._val <= other def __eq__(self, other): return float(self) == float(other) def __neg__(self): return ExtendedInteger(-self.a, -self.b, self.p) def __pos__(self): return ExtendedInteger(+self.a, +self.b, self.p) def __add__(self, other): if isinstance(other, ExtendedInteger): # If both instances have the same p value, # return a new ExtendedInteger instance if self.p == other.p: new_a = self.a + other.a new_b = self.b + other.b return ExtendedInteger(new_a, new_b, self.p) # Otherwise return a float else: return self._val + other._val # If other is integral, add other to self's a value elif isinstance(other, numbers.Integral): new_a = self.a + other return ExtendedInteger(new_a, self.b, self.p) # If other is real, return a float elif isinstance(other, numbers.Real): return self._val + other._val # If other is of unknown type, let other determine # what to do else: return NotImplemented def __radd__(self, other): # Addition is commutative so defer to __add__ return self.__add__(other) def __mul__(self, other): if isinstance(other, ExtendedInteger): # If both instances have the same p value, # return a new ExtendedInteger instance if self.p == other.p: new_a = (self.a * other.a) + (self.b * other.b * self.p) new_b = (self.a * other.b) + (self.b * other.a) return ExtendedInteger(new_a, new_b, self.p) # Otherwise, return a float else: return self._val * other._val # If other is integral, multiply self's a and b by other elif isinstance(other, numbers.Integral): new_a = self.a * other new_b = self.b * other return ExtendedInteger(new_a, new_b, self.p) # If other is real, return a float elif isinstance(other, numbers.Real): return self._val * other # If other is of unknown type, let other determine # what to do else: return NotImplemented def __rmul__(self, other): # Multiplication is commutative so defer to __mul__ return self.__mul__(other) def __pow__(self, exponent): return self._val ** exponent def __rpow__(self, base): return base ** self._val您需要實現許多 dunder 方法以確保具體類型實現 Real 接口。您還必須考慮 .__add__() 和 .__mul__() 等方法如何與其他 Real 類型交互。
實現 ExtendedInteger 後,您現在可以執行以下操作:
>>> a = ExtendedInteger(1, 2)>>> b = ExtendedInteger(2, 3)>>> aExtendedInteger(1, 2, 2)>>> # Check that a is a Number>>> isinstance(a, numbers.Number)True>>> # Check that a is Real>>> isinstance(a, numbers.Real)True>>> print(a)1 + 2√2>>> a * bExtendedInteger(14, 7, 2)>>> print(a * b)14 + 7√2>>> float(a)3.8284271247461903Python 的數字層次結構非常靈活。但是,當然,在實現派生自內置抽象基類型的類型時,您應該始終非常小心。你需要確保他們與其他人相處得很好。
在實現自定義數字類型之前,您應該閱讀類型實現者的文檔中有幾個提示。仔細閱讀 Fraction 的實現也很有幫助。
所以文章你看完了。關於 Python 中的數字,您可能不知道的三件事(可能還有更多):
數字有方法,就像 Python 中的幾乎所有其他對象一樣。
數字有一個層次結構,即使該層次結構被 Decimal 和 float 濫用了一點。
您可以創建適合 Python 數字層次結構的自己的數字。
我希望你學到了一些新東西!
參考鏈接:
3 Things You Might Not Know About Numbers in Python
Python 中有關數字必知的三件事