If you use Python Any coding done , Then you probably used numbers in a program . for example , You might use an integer to specify the index of a value in the list .
however Python The numbers in are not just their original values . Let's take a look at what you may not know about Python Three things about numbers in .
Python There is a concept called : Everything is the object . You are in Python The first object learned in "HelloWorld" Is a representation of a string str object .
Then you learned that strings have methods , for example .lower() Method , It returns a new string of all lowercase characters :
>>> "HELLO".lower()'hello' For example, capital letters capitalize(), Returns a copy of the string , The first character is capitalized , The rest are in lowercase .
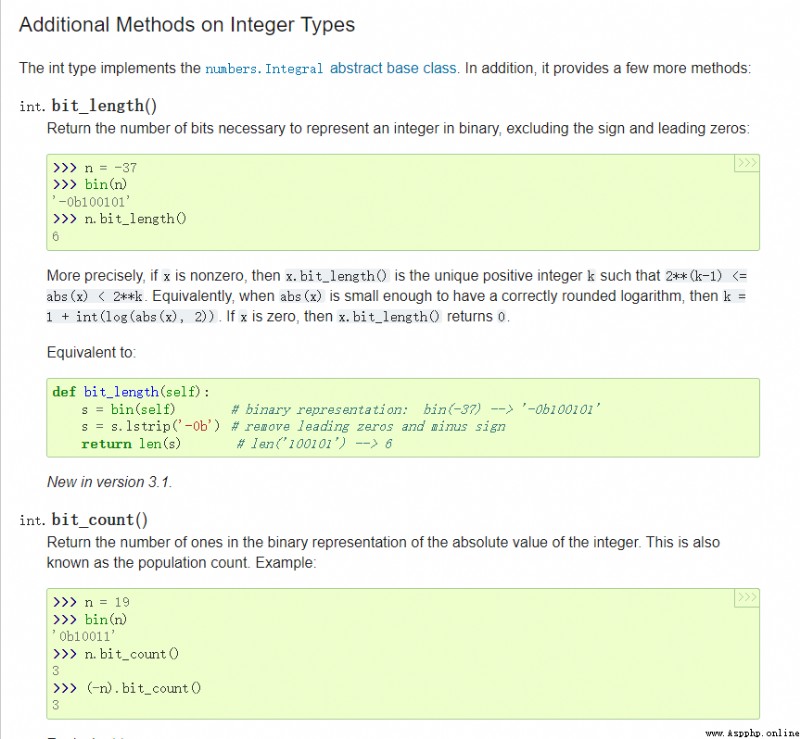
>>> mystring = "hello python">>> print(mystring.capitalize())Hello pythonPython The numbers in are also objects , It's like a string , It has its own way . for example , You can use .to_bytes() Method Convert an integer to Byte string :
>>> n = 255>>> n.to_bytes(length=2, byteorder="big")b'\x00\xff' among ,length Parameter specifies the number of bytes to use in the string ,byteorder Parameter determines the order of bytes . for example , take byteorder Set to “big” Will return a byte string , The most important byte comes first , And will be byteorder Set to "little" Then put the least important byte in the front .
>>> n.to_bytes(length=2, byteorder="little")b'\xff\x00'255 Yes can be expressed as 8 The largest integer of a bit integer , So you can go to .to_bytes() Set in length=1 No problem :
>>> n.to_bytes(length=1, byteorder="big")b'\xff' however , If in .to_bytes() Lieutenant general length=1 Set to 256, Will receive OverflowError error :
>>> n = 256>>> n.to_bytes(length=1, byteorder="big")Traceback (most recent call last): File "<stdin>", line 1, in <module>OverflowError: int too big to convert You can use .from_bytes() Class method converts a byte string to an integer :
>>> int.from_bytes(b'\x06\xc1', byteorder="big")1729 Class method It is called from the class name instead of the class instance , This is the one above int On the call .from_bytes() Reason for method .
Floating point numbers also have methods . Perhaps the most useful method for floating point numbers is .is_integer() , It is used to check whether floating-point numbers have no decimal part :
>>> n = 2.0>>> n.is_integer()True>>> n = 3.14>>> n.is_integer()False An interesting floating point method is .as_integer_ratio() Method , It returns a tuple , It contains the numerator and denominator of the fraction representing the floating-point value :
>>> n = 0.75>>> n.as_integer_ratio()(3, 4)however , because Floating point means error , This method may return some unexpected values :
>>> n = 0.1>>> n.as_integer_ratio()(3602879701896397, 36028797018963968)if necessary , You can call methods on numeric types by enclosing text in parentheses :
>>> (255).to_bytes(length=1, byteorder="big")b'\xff'>>> (3.14).is_integer()False If you don't enclose integer text in parentheses , When you call a method, you will see a SyntaxError —— Though strangely , You don't need parentheses with floating point text :
>>> 255.to_bytes(length=1, byteorder="big") File "<stdin>", line 1 255.to_bytes(length=1, byteorder="big") ^SyntaxError: invalid syntax>>> 3.14.is_integer()FalseYou can go to In the document find Python A complete list of available methods for numeric types :
In mathematics , Numbers have a natural hierarchy . for example , All natural numbers are integers , All integers are rational , All rational numbers are real numbers , All real numbers are plural .
Python The same is true of the numbers in . This “ The digital tower ” adopt numbers modular It contains Abstract type To express .
Python Every number in is Number An instance of a class :
>>> from numbers import Number>>> # Integers inherit from Number>>> isinstance(1729, Number)True>>> # Floats inherit from Number>>> isinstance(3.14, Number)True>>> # Complex numbers inherit from Number>>> isinstance(1j, Number)True If you need to check Python Whether the value in is a number , But you don't care what kind of number the value is , Please use isinstance(value, Number).
Python Comes with four additional abstract types , The hierarchy starts with the most common number type , As shown below :
Complex Class is used to represent complex numbers . There is a built-in concrete Complex type :complex.
Real Class is used to represent real numbers . There is a built-in concrete Real type :float.
Rational Class is used to represent rational numbers . There is a built-in concrete Rational type :Fraction.
Integral Class is used to represent integers . There are two built-in concrete Integral type :int and bool.
You can verify all this in your terminal :
>>> import numbers>>> # Complex numbers inherit from Complex>>> isinstance(1j, numbers.Complex)True>>> # Complex numbers are not Real>>> isinstance(1j, numbers.Real)False>>> # Floats are Real>>> isinstance(3.14, numbers.Real)True>>> # Floats are not Rational>>> isinstance(3.14, numbers.Rational)False>>> # Fractions are Rational>>> from fractions import Fraction>>> isinstance(Fraction(1, 2), numbers.Rational)True>>> # Fractions are not Integral>>> isinstance(Fraction(1, 2), numbers.Integral)False>>> # Ints are Integral>>> isinstance(1729, numbers.Integral)True>>> # Bools are Integral>>> isinstance(True, numbers.Integral)True>>> True == 1True>>> False == 0Truehowever , Take a closer look at , A few things are right Python The number hierarchy of is a little weird .
Python There are four specific numerical types corresponding to the four abstract types in the digital tower :complex, float, Fraction, and int.
however Python There is a fifth number type , namely Decimal class , Used to accurately represent decimal numbers and overcome the limitations of floating-point operations .
As you might guess Decimal Number is a real number , But you are wrong :
>>> from decimal import Decimal>>> import numbers>>> isinstance(Decimal("3.14159"), numbers.Real)False in fact ,Decimal The only type that a number inherits from is Python Of Number class :
>>> isinstance(Decimal("3.14159"), numbers.Complex)False>>> isinstance(Decimal("3.14159"), numbers.Rational)False>>> isinstance(Decimal("3.14159"), numbers.Integral)False>>> isinstance(Decimal("3.14159"), numbers.Number)TrueDecimal Do not inherit from Integral That makes sense . In a way ,Decimal Do not inherit from Rational It also makes sense . But why Decimal Not from Real or Complex Inheritance ?
The answer lies in CPython Source code in :
Decimal have Real abc All methods specified , But it should not be registered as Real, Because decimals do not interoperate with binary floating-point numbers ( for example :Decimal('3.14') + 2.71828 Is not supported ). however , Abstract real numbers are expected to be interoperable ( namely , If R1 and R2 All are real numbers. , be R1 + R2 Should be able to work ).
It all boils down to achieving .
On the other hand , Floating point numbers implement Real Abstract base class of , And used to represent real numbers . however , Due to limited memory constraints , Floating point numbers are only finite approximations of real numbers . It's confusing , As follows :
>>> 0.1 + 0.1 + 0.1 == 0.3FalseFloating point numbers are stored in memory as binary fractions , But this can cause some problems .
It's like fractions 1/3 There is no finite decimal representation —— There are countless three after the decimal point .
fraction 1/10 There is no finite binary fraction representation . let me put it another way , You can't just Precise precision will 0.1 Stored on the computer On —— Unless that computer has unlimited memory .
From a strictly mathematical point of view , All floating point numbers are rational numbers —— except float("inf") and float("nan"). But programmers use them to approximate real numbers and treat them as real numbers in most cases .
float("nan") Is a special floating point value , Express “ The digital ” value —— Commonly abbreviated as NaN value . But because of float It's the number type , therefore isinstance(float("nan"), Number) return True
you 're right :“ Not numbers ” Value is number .("not a number" values are numbers.)
This is the strange thing about floating point numbers .
Python The abstract number base type of allows you to create your own custom abstract and concrete number types .
It is using Python About the types of numbers in , such as numbers The type of , You can define other numeric objects with special properties and methods .
for example , Consider the following classes ExtendedInteger, It has achieved a+b \sqrt p Numbers in form , among a and b Is an integer ,p Prime number ( Please note that , Class does not enforce primes ):
import mathimport numbersclass ExtendedInteger(numbers.Real): def __init__(self, a, b, p = 2) -> None: self.a = a self.b = b self.p = p self._val = a + (b * math.sqrt(p)) def __repr__(self): return f"{self.__class__.__name__}({self.a}, {self.b}, {self.p})" def __str__(self): return f"{self.a} + {self.b}√{self.p}" def __trunc__(self): return int(self._val) def __float__(self): return float(self._val) def __hash__(self): return hash(float(self._val)) def __floor__(self): return math.floor(self._val) def __ceil__(self): return math.ceil(self._val) def __round__(self, ndigits=None): return round(self._val, ndigits=ndigits) def __abs__(self): return abs(self._val) def __floordiv__(self, other): return self._val // other def __rfloordiv__(self, other): return other // self._val def __truediv__(self, other): return self._val / other def __rtruediv__(self, other): return other / self._val def __mod__(self, other): return self._val % other def __rmod__(self, other): return other % self._val def __lt__(self, other): return self._val < other def __le__(self, other): return self._val <= other def __eq__(self, other): return float(self) == float(other) def __neg__(self): return ExtendedInteger(-self.a, -self.b, self.p) def __pos__(self): return ExtendedInteger(+self.a, +self.b, self.p) def __add__(self, other): if isinstance(other, ExtendedInteger): # If both instances have the same p value, # return a new ExtendedInteger instance if self.p == other.p: new_a = self.a + other.a new_b = self.b + other.b return ExtendedInteger(new_a, new_b, self.p) # Otherwise return a float else: return self._val + other._val # If other is integral, add other to self's a value elif isinstance(other, numbers.Integral): new_a = self.a + other return ExtendedInteger(new_a, self.b, self.p) # If other is real, return a float elif isinstance(other, numbers.Real): return self._val + other._val # If other is of unknown type, let other determine # what to do else: return NotImplemented def __radd__(self, other): # Addition is commutative so defer to __add__ return self.__add__(other) def __mul__(self, other): if isinstance(other, ExtendedInteger): # If both instances have the same p value, # return a new ExtendedInteger instance if self.p == other.p: new_a = (self.a * other.a) + (self.b * other.b * self.p) new_b = (self.a * other.b) + (self.b * other.a) return ExtendedInteger(new_a, new_b, self.p) # Otherwise, return a float else: return self._val * other._val # If other is integral, multiply self's a and b by other elif isinstance(other, numbers.Integral): new_a = self.a * other new_b = self.b * other return ExtendedInteger(new_a, new_b, self.p) # If other is real, return a float elif isinstance(other, numbers.Real): return self._val * other # If other is of unknown type, let other determine # what to do else: return NotImplemented def __rmul__(self, other): # Multiplication is commutative so defer to __mul__ return self.__mul__(other) def __pow__(self, exponent): return self._val ** exponent def __rpow__(self, base): return base ** self._val You need to implement many dunder Method to ensure that the concrete type implements Real Interface . You must also consider .__add__() and .__mul__() And other methods Real Type interaction .
Realization ExtendedInteger after , You can now do the following :
>>> a = ExtendedInteger(1, 2)>>> b = ExtendedInteger(2, 3)>>> aExtendedInteger(1, 2, 2)>>> # Check that a is a Number>>> isinstance(a, numbers.Number)True>>> # Check that a is Real>>> isinstance(a, numbers.Real)True>>> print(a)1 + 2√2>>> a * bExtendedInteger(14, 7, 2)>>> print(a * b)14 + 7√2>>> float(a)3.8284271247461903Python Our digital hierarchy is very flexible . however , Of course , When implementing a type that derives from a built-in abstract base type , You should always be very careful . You need to make sure they get along well with others .
Before implementing custom numeric types , You should read the documentation for the type implementer There are a few tips . Read... Carefully Fraction Of Realization It's also helpful .
So you have read the article . About Python Number in , Three things you may not know ( There may be more ):
Digital method , It's like Python Like almost all other objects in .
Numbers have a hierarchy , Even if the hierarchy is Decimal and float A bit of abuse .
You can create a suitable Python The number hierarchy's own number .
I hope you learned something new !
Reference link :
3 Things You Might Not Know About Numbers in Python
Python Three things you must know about numbers in