分類算法：C4.5，樸素貝葉斯（Naive Bayes），SVM，KNN，Adaboost，CARTl 。聚類算法：K-Means，EMl 。關聯分析：Aprioril 。連接分析：PageRank

文章目錄

• 准備數據
• 一、C4.5 算法
• 二、CART 算法
• 三、SVM 算法
• 四、KNN算法
• 五、AdaBoost算法
• 六、Apriori算法
• 七、K-Means算法
• 八、樸素貝葉斯（Naive Bayes）算法
• 九、EM算法
• 十、PageRank算法
• 十一、隨機森林（Random Forest）算法
• 總結

准備數據

我們統一用鸢尾花作為測試數據以便能對比各個算法的性能。

國際權威的學術組織 ICDM （the IEEE International Conference on Data Mining）評選出了十大經典的算法。按照不同的目的，我可以將這些算法分成四類。

分類算法：C4.5（ID3），樸素貝葉斯（Naive Bayes），SVM，KNN，Adaboost，CARTl ,randomForest,bugging
聚類算法：K-Means，EMl
關聯分析：Aprioril
連接分析：PageRank

一、C4.5 算法

C4.5 是決策樹的算法，它創造性地在決策樹構造過程中就進行了剪枝，並且可以處理連續的屬性，也能對不完整的數據進行處理。它可以說是決策樹分類中，具有裡程碑式意義的算法。
信息熵（entropy）的概念，它表示了信息的不確定度.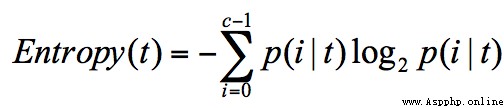

ID3 算法計算的是信息增益，信息增益指的就是劃分可以帶來純度的提高，信息熵的下降。它的計算公式，是父親節點的信息熵減去所有子節點的信息熵。在計算的過程中，我們會計算每個子節點的歸一化信息熵，即按照每個子節點在父節點中出現的概率，來計算這些子節點的信息熵。所以信息增益的公式可以表示為：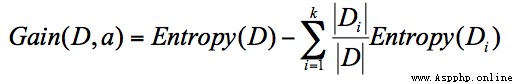

公式中 D 是父親節點，Di 是子節點，Gain(D,a) 中的 a 作為 D 節點的屬性選擇。
ID3 就是要將信息增益最大的節點作為父節點，這樣可以得到純度高的決策樹，所以我們將信息增益最大的節點作為根節點。ID3 的算法規則相對簡單，可解釋性強。同樣也存在缺陷，比如我們會發現 ID3 算法傾向於選擇取值比較多的屬性。
ID3 有一個缺陷就是，有些屬性可能對分類任務沒有太大作用，但是他們仍然可能會被選為最優屬性。
C4.5 都在哪些方面改進了 ID3 呢？
C4.5 采用信息增益率的方式來選擇屬性。信息增益率 = 信息增益 / 屬性熵。
ID3 構造決策樹的時候，容易產生過擬合的情況。在 C4.5 中，會在決策樹構造之後采用悲觀剪枝（PEP），這樣可以提升決策樹的泛化能力。悲觀剪枝是後剪枝技術中的一種，通過遞歸估算每個內部節點的分類錯誤率，比較剪枝前後這個節點的分類錯誤率來決定是否對其進行剪枝。這種剪枝方法不再需要一個單獨的測試數據集。
針對數據集不完整的情況，C4.5 也可以進行處理。
C4.5 需要對數據集進行多次掃描，算法效率相對較低。
代碼：

from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
X,y = load_iris(return_X_y=True)
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=0.33,random_state=0)
clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(train_X,train_y)
print(clf.score(test_X,test_y))

准確率：96%

二、CART 算法

當基尼系數越小的時候，說明樣本之間的差異性小，不確定程度低。分類的過程本身是一個不確定度降低的過程，即純度的提升過程。所以 CART 算法在構造分類樹的時候，會選擇基尼系數最小的屬性作為屬性的劃分。

GINI 系數的計算公式：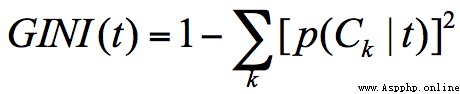

節點 D 的基尼系數等於子節點 D1 和 D2 的歸一化基尼系數之和，用公式表示為：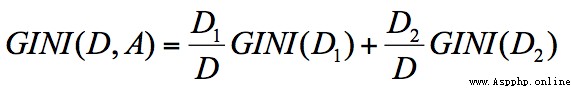

from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
X,y = load_iris(return_X_y=True)
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=0.33,random_state=0)
clf = tree.DecisionTreeClassifier(criterion="gini")
clf = clf.fit(train_X,train_y)
print(clf.score(test_X,test_y))

准確率：96%

三、SVM 算法

SVM 的中文叫支持向量機，英文是 Support Vector Machine，簡稱 SVM。SVM 在訓練中建立了一個超平面的分類模型。
能存在多個最優決策面，它們都能把數據集正確分開，這些最優決策面的分類間隔可能是不同的，而那個擁有“最大間隔”（max margin）的決策面就是 SVM 要找的最優解。
非線性 SVM 中，核函數的選擇就是影響 SVM 最大的變量。最常用的核函數有線性核、多項式核、高斯核、拉普拉斯核、sigmoid 核，或者是這些核函數的組合。這些函數的區別在於映射方式的不同。通過這些核函數，我們就可以把樣本空間投射到新的高維空間中。
SVM 最主要的思想就是硬間隔、軟間隔和核函數.
kernel 代表核函數的選擇，它有四種選擇，只不過默認是 rbf，即高斯核函數。
linear：線性核函數
poly：多項式核函數
rbf：高斯核函數（默認）
sigmoid：sigmoid 核函數這四種函數代表不同的映射方式，如何選擇這 4 種核函數呢？
線性核函數，是在數據線性可分的情況下使用的，運算速度快，效果好。不足在於它不能處理線性不可分的數據。
多項式核函數可以將數據從低維空間映射到高維空間，但參數比較多，計算量大。
高斯核函數同樣可以將樣本映射到高維空間，但相比於多項式核函數來說所需的參數比較少，通常性能不錯，所以是默認使用的核函數。
了解深度學習的同學應該知道 sigmoid 經常用在神經網絡的映射中。因此當選用 sigmoid 核函數時，SVM 實現的是多層神經網絡。

from sklearn import svm
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X,y = load_iris(return_X_y=True)
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=0.33,random_state=0)
# 采用Z-Score規范化數據，保證每個特征維度的數據均值為0，方差為1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)
clf = svm.SVC(kernel='rbf')
clf = clf.fit(train_X,train_y)
print(clf.score(test_X,test_y))

准確率96%。

四、KNN算法

KNN 也叫 K 最近鄰算法，英文是 K-Nearest Neighbor。所謂 K 近鄰，就是每個樣本都可以用它最接近的 K 個鄰居來代表。如果一個樣本，它的 K 個最接近的鄰居都屬於分類 A，那麼這個樣本也屬於分類 A。
KNN 的工作原理。整個計算過程分為三步：
計算待分類物體與其他物體之間的距離；
統計距離最近的 K 個鄰居；
對於 K 個最近的鄰居，它們屬於哪個分類最多，待分類物體就屬於哪一類。
交叉驗證的思路就是，把樣本集中的大部分樣本作為訓練集，剩余的小部分樣本用於預測，來驗證分類模型的准確性。所以在 KNN 算法中，我們一般會把 K 值選取在較小的范圍內，同時在驗證集上准確率最高的那一個最終確定作為 K 值。
KNN算法是機器學習中最簡單的算法之一，但是工程實現上，如果訓練樣本過大，則傳統的遍歷全樣本尋找k近鄰的方式將導致性能的急劇下降。 因此，為了優化效率，不同的訓練數據存儲結構被納入到實現方式之中。在sikit-learn中的KNN算法參數也提供了’kd_tree’之類的算法選擇項。
n_neighbors：默認為5，就是k-NN的k的值，選取最近的k個點。
weights：默認是uniform，參數可以是uniform、distance

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X,y = load_iris(return_X_y=True)
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=0.33,random_state=0)
# 采用Z-Score規范化數據，保證每個特征維度的數據均值為0，方差為1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)
clf = KNeighborsClassifier(n_neighbors=5,algorithm='kd_tree',weights='uniform')
clf = clf.fit(train_X,train_y)
print(clf.score(test_X,test_y))

五、AdaBoost算法

Adaboost 在訓練中建立了一個聯合的分類模型。boost 在英文中代表提升的意思，所以 Adaboost 是個構建分類器的提升算法。它可以讓我們多個弱的分類器組成一個強的分類器，所以 Adaboost 也是一個常用的分類算法。
算法通過訓練多個弱分類器，將它們組合成一個強分類器，也就是我們俗話說的“三個臭皮匠，頂個諸葛亮”。

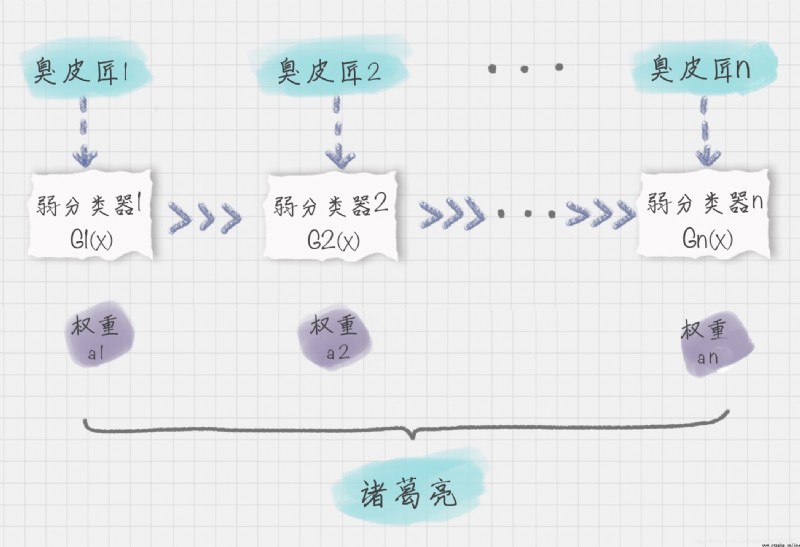
假設弱分類器為 Gi​(x)，它在強分類器中的權重 αi​，那麼就可以得出強分類器 f(x)：

如果弱分類器的分類效果好，那麼權重應該比較大，如果弱分類器的分類效果一般，權重應該降低。所以我們需要基於這個弱分類器對樣本的分類錯誤率來決定它的權重，用公式表示就是：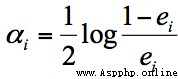

其中 ei​ 代表第 i 個分類器的分類錯誤率。
AdaBoost 算法是通過改變樣本的數據分布來實現的。AdaBoost 會判斷每次訓練的樣本是否正確分類，對於正確分類的樣本，降低它的權重，對於被錯誤分類的樣本，增加它的權重。再基於上一次得到的分類准確率，來確定這次訓練樣本中每個樣本的權重。然後將修改過權重的新數據集傳遞給下一層的分類器進行訓練。這樣做的好處就是，通過每一輪訓練樣本的動態權重，可以讓訓練的焦點集中到難分類的樣本上，最終得到的弱分類器的組合更容易得到更高的分類准確率。

n_estimators：算法的最大迭代次數，也是分類器的個數，每一次迭代都會引入一個新的弱分類器來增加原有的分類器的組合能力。默認是 50。

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import *
X,y = load_iris(return_X_y=True)
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=0.33,random_state=0)
# 采用Z-Score規范化數據，保證每個特征維度的數據均值為0，方差為1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)
clf = AdaBoostClassifier(base_estimator=DecisionTreeClassifier(),n_estimators=50)
clf = clf.fit(train_X,train_y)
pre_y = clf.predict(test_X)
for i,j in zip(pre_y,test_y):
print(i,j)
print('%.4lf'%accuracy_score(pre_y,test_y))

准確率：96%。
AdaBoost是串行的多個弱分類器組合，還有一類是並行的弱分類器組合，叫Bagging，代表是隨機森林。

六、Apriori算法

Apriori 是一種挖掘關聯規則（association rules）的算法，它通過挖掘頻繁項集（frequent item sets）來揭示物品之間的關聯關系，被廣泛應用到商業挖掘和網絡安全等領域中。頻繁項集是指經常出現在一起的物品的集合，關聯規則暗示著兩種物品之間可能存在很強的關系。
Apriori 算法其實就是查找頻繁項集 (frequent itemset) 的過程。頻繁項集就是支持度大於等於最小支持度 (Min Support) 阈值的項集，所以小於最小值支持度的項目就是非頻繁項集，算法進行刪除，而大於等於最小支持度的項集就是頻繁項集，然後做進一步劃分。
Apriori 在計算的過程中有以下幾個缺點：可能產生大量的候選集。因為采用排列組合的方式，把可能的項集都組合出來了；每次計算都需要重新掃描數據集，來計算每個項集的支持度。
所以 Apriori 算法會浪費很多計算空間和計算時間，為此人們提出了 FP-Growth 算法，它的特點是：創建了一棵 FP 樹來存儲頻繁項集。在創建前對不滿足最小支持度的項進行刪除，減少了存儲空間。整個生成過程只遍歷數據集 2 次，大大減少了計算量。所以在實際工作中，我們常用 FP-Growth 來做頻繁項集的挖掘，下面我給你簡述下 FP-Growth 的原理。
FP就是根據結果出現的頻繁數進行構建的，構建過程如下問：FP-Growth

from efficient_apriori import apriori
data = [['牛奶','面包','尿布'], ['可樂','面包', '尿布', '啤酒'],
['牛奶','尿布', '啤酒', '雞蛋'], ['面包', '牛奶', '尿布',
'啤酒'], ['面包', '牛奶', '尿布', '可樂']]
itemsets ,rules = apriori(data,min_support=0.5,min_confidence=1)
print(itemsets)
print(rules)

輸出有關聯度的列表：

[{
牛奶} -> {
尿布}, {
面包} -> {
尿布}, {
啤酒} -> {
尿布}, {
牛奶, 面包} -> {
尿布}]

七、K-Means算法

K-Means 算法是一個聚類算法。想把物體劃分成 K 類。假設每個類別裡面，都有個“中心點”，它是這個類別的核心。現在有一個新點要歸類，這時候就只要計算這個新點與 K 個中心點的距離，距離哪個中心點近，就變成了哪個類別。
K-Means是無監督學習，隨機指定質心，然後迭代更新質心位置，知道所有點不在發生劃分改變為止。

from sklearn.preprocessing import StandardScaler
from sklearn.metrics import *
X,y = load_iris(return_X_y=True)
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=0.33,random_state=0)
# 采用Z-Score規范化數據，保證每個特征維度的數據均值為0，方差為1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)
clf = KMeans(n_clusters=3,max_iter=300)
clf = clf.fit(train_X,train_y)
pre_y = clf.predict(test_X)
# for i,j in zip(pre_y,test_y):
# print(i,j)
print('%.4lf'%accuracy_score(pre_y,test_y))

八、樸素貝葉斯（Naive Bayes）算法

算法原理：利用貝葉斯公式計算特征的概率，也就是利用先驗概率和後驗概率的結合，概率大的作為分類結果。
貝葉斯公式：

換個表達形式就會明朗很多，如下：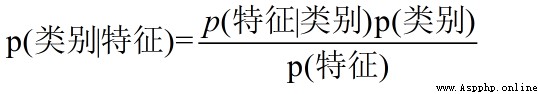

我們最終求得p(類別|特征)即可！而又可以轉化為利用已經有的數據，計算後驗概率和先驗概率。也就是已經有的測試數據樣本的統計信息，便可以得到p(類別|特征)的值。詳解

sklearn 機器學習包sklearn 的全稱叫 Scikit-learn，它給我們提供了 3 個樸素貝葉斯分類算法，分別是高斯樸素貝葉斯（GaussianNB）、多項式樸素貝葉斯（MultinomialNB）和伯努利樸素貝葉斯（BernoulliNB）。這三種算法適合應用在不同的場景下，我們應該根據特征變量的不同選擇不同的算法：
高斯樸素貝葉斯：特征變量是連續變量，符合高斯分布，比如說人的身高，物體的長度。
多項式樸素貝葉斯：特征變量是離散變量，符合多項分布，在文檔分類中特征變量體現在一個單詞出現的次數，或者是單詞的 TF-IDF 值等。
伯努利樸素貝葉斯：特征變量是布爾變量，符合 0/1 分布，在文檔分類中特征是單詞是否出現。

樸素貝葉斯模型是基於概率論的原理，它的思想是這樣的：對於給出的未知物體想要進行分類，就需要求解在這個未知物體出現的條件下各個類別出現的概率，哪個最大，就認為這個未知物體屬於哪個分類。
貝葉斯原理、貝葉斯分類和樸素貝葉斯這三者之間是有區別：貝葉斯原理是最大的概念，它解決了概率論中“逆向概率”的問題，在這個理論基礎上，人們設計出了貝葉斯分類器，樸素貝葉斯分類是貝葉斯分類器中的一種，也是最簡單，最常用的分類器。
樸素貝葉斯之所以樸素是因為它假設屬性是相互獨立的，因此對實際情況有所約束，如果屬性之間存在關聯，分類准確率會降低。不過好在對於大部分情況下，樸素貝葉斯的分類效果都不錯。
樸素貝葉斯分類常用於文本分類，尤其是對於英文等語言來說，分類效果很好。它常用於垃圾文本過濾、情感預測、推薦系統等。

from sklearn.naive_bayes import MultinomialNB
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
X,y = load_iris(return_X_y=True)
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=0.33,random_state=0)
clf = MultinomialNB(alpha=0.001)
clf = clf.fit(train_X,train_y)
print(clf.score(test_X,test_y))

准確率70%。用的是多項式貝葉斯。
如果用高斯貝葉斯:

from sklearn.naive_bayes import MultinomialNB,GaussianNB
clf = GaussianNB()

准確率96%。

九、EM算法

EM 的英文是 Expectation Maximization，所以 EM 算法也叫最大期望算法。，是求參數的最大似然估計的一種方法。
原理是這樣的：假設我們想要評估參數 A 和參數 B，在開始狀態下二者都是未知的，並且知道了 A 的信息就可以得到 B 的信息，反過來知道了 B 也就得到了 A。可以考慮首先賦予 A 某個初值，以此得到 B 的估值，然後從 B 的估值出發，重新估計 A 的取值，這個過程一直持續到收斂為止。EM 算法經常用於聚類和機器學習領域中。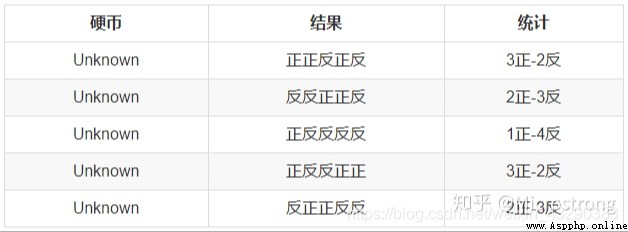

首先，隨機選取 PA=正面 PB =正面 的初始值。EM算法的E步驟，是計算在當前的預估參數下，隱含變量（是A硬幣還是B硬幣）的每個值出現的概率，取最大概率的那個座位本次實驗是A還是B。

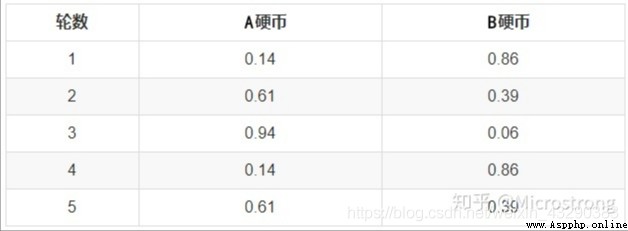
from sklearn.mixture import GaussianMixture
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import *
X,y = load_iris(return_X_y=True)
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=0.33,random_state=0)
# 采用Z-Score規范化數據，保證每個特征維度的數據均值為0，方差為1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)
clf = GaussianMixture(n_components=3)
clf = clf.fit(train_X,train_y)
pre_y = clf.predict(test_X)
# for i,j in zip(pre_y,test_y):
# print(i,j)
print('%.4lf'%accuracy_score(pre_y,test_y))

十、PageRank算法

PageRank 起源於論文影響力的計算方式，如果一篇文論被引入的次數越多，就代表這篇論文的影響力越強。同樣 PageRank 被 Google 創造性地應用到了網頁權重的計算中：當一個頁面鏈出的頁面越多，說明這個頁面的“參考文獻”越多，當這個頁面被鏈入的頻率越高，說明這個頁面被引用的次數越高。基於這個原理，我們可以得到網站的權重劃分。
假設一共有 4 個網頁 A、B、C、D。它們之間的鏈接信息如圖所示：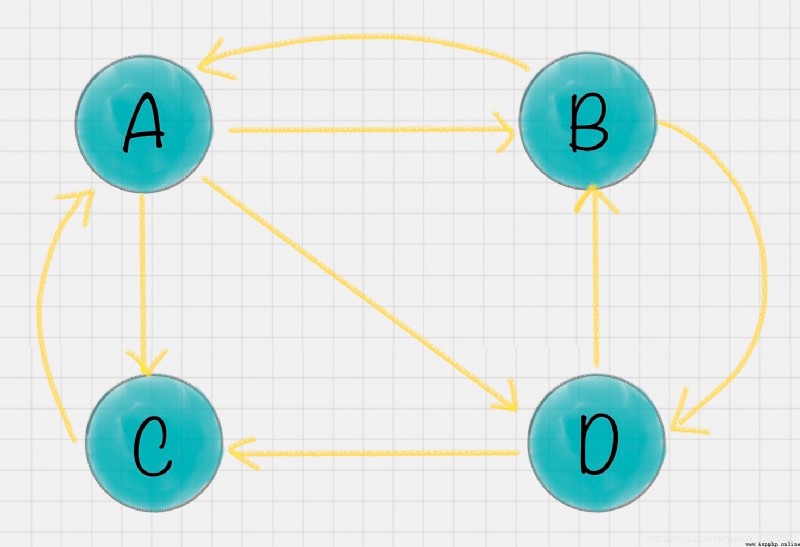

一個網頁的影響力 = 所有入鏈集合的頁面的加權影響力之和，用公式表示為：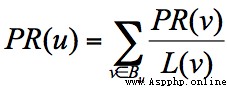

例子中，你能看到 A 有三個出鏈分別鏈接到了 B、C、D 上。那麼當用戶訪問 A 的時候，就有跳轉到 B、C 或者 D 的可能性，跳轉概率均為 1/3。B 有兩個出鏈，鏈接到了 A 和 D 上，跳轉概率為 1/2。這樣，我們可以得到 A、B、C、D 這四個網頁的轉移矩陣 M：

假設 A、B、C、D 四個頁面的初始影響力都是相同的，即：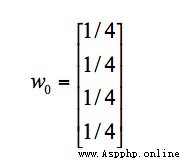
當進行第一次轉移之後，各頁面的影響力 w1​ 變為：

然後我們再用轉移矩陣乘以 w1​ 得到 w2​ 結果，直到第 n 次迭代後 wn​ 影響力不再發生變化，可以收斂到 (0.3333，0.2222，0.2222，0.2222），也就是對應著 A、B、C、D 四個頁面最終平衡狀態下的影響力。
A 頁面相比於其他頁面來說權重更大，也就是 PR 值更高。而 B、C、D 頁面的 PR 值相等。

import networkx as nx
# 創建有向圖
G = nx.DiGraph()
# 有向圖之間邊的關系
edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "A"), ("B", "D"), ("C", "A"), ("D", "B"), ("D", "C")]
for edge in edges:
G.add_edge(edge[0], edge[1])
pagerank_list = nx.pagerank(G, alpha=1)
print("pagerank值是：", pagerank_list)

結果：

pagerank值是： {
'A': 0.33333396911621094, 'B': 0.22222201029459634, 'C': 0.22222201029459634, 'D': 0.22222201029459634}

十一、隨機森林（Random Forest）算法

隨機森林就是通過集成學習的思想：將多棵樹並行集成的一種算法，它的基本單元是決策樹，而它的本質屬於機器學習的一大分支——集成學習（Ensemble Learning）方法。
隨機森林的名稱中有兩個關鍵詞，一個是“隨機”，一個就是“森林”。“森林”我們很好理解，一棵叫做樹，那麼成百上千棵就可以叫做森林了，這樣的比喻還是很貼切的，其實這也是隨機森林的主要思想–集成思想的體現。
“隨機”的含義是：如果訓練集大小為N，對於每棵樹而言，隨機且有放回地從訓練集中的抽取N個訓練樣本（這種采樣方式稱為bootstrap sample方法），作為該樹的訓練集。詳解

from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import *
X,y = load_iris(return_X_y=True)
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size=0.33,random_state=0)
# 采用Z-Score規范化數據，保證每個特征維度的數據均值為0，方差為1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)
clf = RandomForestClassifier(n_jobs=-1)
clf = clf.fit(train_X,train_y)
pre_y = clf.predict(test_X)
# for i,j in zip(pre_y,test_y):
# print(i,j)
print('%.4lf'%accuracy_score(pre_y,test_y))

總結

了解基本算法原理，盡管我們親自實現算法的可能性不大，了解算法還是挺有用。