Python Development -- 16 collection type built-in methods

List of articles

• • One . purpose
  • • 1. Relationship between operation
    • 2. duplicate removal
  • Two . Define the way
  • 3、 ... and . Type conversion
  • Four . Common operations
  • Relationship between operation
  • • 1. intersection : `&`, `.intersection()`
    • 2. Combine : `|`, `.union()`
    • 3. Difference set : `-`, `.difference()`
    • 4. Symmetric difference set : `^`, `.symmetric_difference()`
    • 5. Superset ：`>=`, `.issuperset()`
    • 6. A subset of : `<=`, `.issubset()`
  • duplicate removal
  • • 1. Simple de duplication ( There is no guarantee of order )
    • 2. Remove the duplicate and keep the original order ( understand )
  • 5、 ... and . Built-in methods
  • Priority operation (*********)
  • • 1. length : .len( )
    • 2. Members of the operation in and not in
    • 3. Value cycle
  • Operations that need to be mastered (****)
  • • 1. to update .update( )
    • 2. add to .add( )
    • 3. Take a value .pop( )
    • 4. Delete .remove( ), .discard( )
    • 5. No intersection .isdisjoint( )
  • Operations that don't need to know much (***)
  • • 1..difference_update( )
    • 2..intersection_ update( )
    • 3..symmetric_ difference_ update( )
  • 6、 ... and . summary
  • • You can store multiple values
    • • disorder
      • Variable type ---> must not hash type

One . purpose

1. Relationship between operation

• intersection : &
• Combine : |
• Difference set : -
• Cross complement : ^

2. duplicate removal

• A simple example

l = [1,1,2,2,1,3]
s = set(l)
print(list(s)) #[1,2,3]

Two . Define the way

• stay “{ }” Separate the elements with commas
  \1. The element of the collection must be of immutable type
  \2. The elements in a set are out of order
  \3. The elements in the collection are unique
• A collection of " factory " : set

s={
1,2,3,4,4,4,4,4,4,4,'a'}
# The operation behind it is 
s=set({
1,2,3,4,'a'})
# If the elements repeat , Only one will be taken 
print(type(s),s)
#<class 'set'> {1, 2, 3, 4, 'a'}
# Add variable type error 
s={
[1,2,3],'aa'} # Report errors 
# A disorderly 
s = {
1,2,"b",4,"a",6,7}
print(s) #{1, 2, 4, 6, 7, 'b', 'a'}

ps : Define empty sets And Define an empty dictionary

# Define empty sets 
s = set()
print(s,type(s))
#set() <class 'set'>
# Define an empty dictionary 
dic = {
}
print(dic,type(dic))
#{} <class 'dict'>

3、 ... and . Type conversion

• As long as there are mutable types, you can't convert , Will report a mistake
• We talk about dictionaries key It's an immutable type , value It's any type , So it's a dictionary when you convert key, instead of value

# integer ---> aggregate 
# res = set({1, 2, 3, 4})
res = {
1, 2, 3, 4}
print(res, type(res))
# {1, 2, 3, 4} <class 'set'>
# floating-point ---> aggregate 
# res1 = set({1.1, 2.2, 3.3, 4.4})
res = {
1.1, 2.2, 3.3, 4.4}
print(res, type(res))
# {1.1, 2.2, 3.3, 4.4} <class 'set'>
# character string ---> aggregate 
res = set('shawn')
print(res, type(res))
# {'a', 'h', 'n', 'w', 's'} <class 'set'>
# Tuples ---> aggregate 
res = set((1, 2, 3, (1, 2, 3)))
print(res, type(res))
# {1, 2, 3, (1, 2, 3)} <class 'set'>
# Dictionaries ---> aggregate 
What's in the dictionary is the collection key ( immutable )
res = set({
'name':'shawn','age':22})
print(res, type(res))
# {'name', 'age'} <class 'set'>
# integer 、 floating-point 、 character string 、 Tuples 、 comprehensive ---> aggregate 
res = set((2, 1.1,"song", (111, 222)))
print(res, type(res))
#{1.1, 2, (111, 222), 'song'} <class 'set'>
When there is a dictionary in the synthesis ( Variable type ) You can't convert , And report an error
res = set((2, 1.1,"song", (111, 222),{
'name': 'shawn', 'age': 22}))
print(res, type(res)) # Report errors 

Four . Common operations

Relationship between operation

# After that, we will explain it with the following example 
linux=["song","hai","xing","shawn","shang"] # learn Linux Of the students 
python=["shang","hai","qing","pu","qu","hi"] # learn Python Of the students 
# Use "for" Loop out two students who have learned both 
linux_python=[]
for s in linux:
if s in python: # Two students who study both 
linux_python.append(s) # Add it to the list 
print(linux_python) #["shang","hai"]

• The illustration

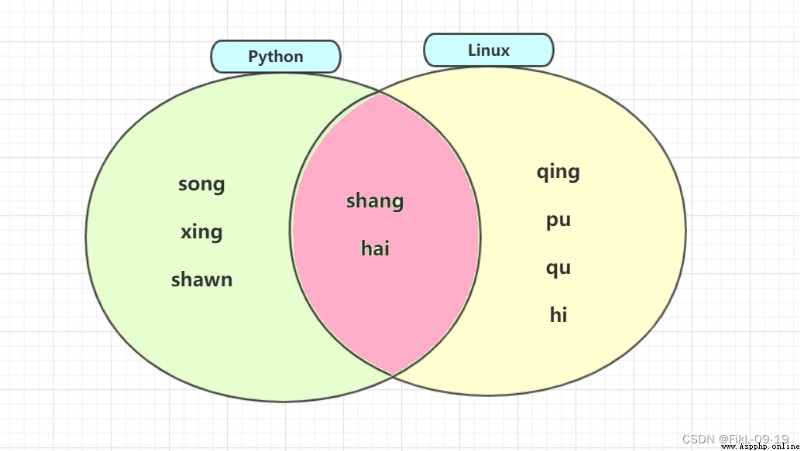
1. intersection : &, .intersection()

# Take out the students who study both courses 
linux={
"song","hai","xing","shawn","shang",}
python={
"shang","hai","qing","pu","qu","hi"}
print(linux & python) #["shang","hai"]
print(linux.intersection(python)) #["shang","hai"]

2. Combine : |, .union()

# Take out all the students 
print(linux | python)
#{'shawn', 'qing', 'hai', 'song', 'hi', 'qu', 'xing', 'shang', 'pu'}
print(linux.union(python))
#{'shawn', 'qing', 'hai', 'song', 'hi', 'qu', 'xing', 'shang', 'pu'}

3. Difference set : -, .difference()

# Just learn "linux" Of , No learning "python" Of ( stay "linux" Look in the class )
print(linux - python) #{'song', 'xing', 'shawn'}
print(linux.difference(python)) #{'song', 'xing', 'shawn'}
# Just learn "python" Of , No learning "linux" Of ( stay "python" Look in the class )
print(python - linux) #{'qing', 'qu', 'hi', 'pu'}
print(python.difference(linux)) #{'qing', 'qu', 'hi', 'pu'}

4. Symmetric difference set : ^, .symmetric_difference()

# The two classes add up to look at the students who have only studied one course 
print(stus_linux ^ stus_python)
# {'pu', 'qing', 'shawn', 'xing', 'song', 'qu', 'hi'}
print(stus_linux.symmetric_difference(stus_python))
# {'pu', 'qing', 'shawn', 'xing', 'song', 'qu', 'hi'}

5. Superset ：>=, .issuperset()

 s1={
1,2,3,4,5}
s2={
3,2,1}
print(s1 >= s2) #True
print(s1.issuperset(s2)) #True

6. A subset of : <=, .issubset()

print(s2 <= s1)
print(s2.issubset(s1))

ps ： If two are the same , Then they are father-child sets

duplicate removal

1. Simple de duplication ( There is no guarantee of order )

s1=set('hello')
print(s1) #{'l','h','o','e'}
# Duplicate a list 
l=['a','b',1,'a','a']
print(list(set(l))) # First of all, it becomes a collection to remove the weight , Again list Become a list 
#[1,'a','b'] There is no guarantee of order 

2. Remove the duplicate and keep the original order ( understand )

l = ['a', 'b', 1, 'a', 'a']
l2=[]
s=set()
# adopt "for" Loop one by one take , Add... One by one 
for item in l:
if item not in s:
l2.append(item) #l2=['a','b',1] Add in one by one 
print(l2) #['a','b','1']

5、 ... and . Built-in methods

Priority operation (*********)

1. length : .len( )

s1={
1,'a','b','c','d'}
print(len(s1)) #5

2. Members of the operation in and not in

s1={
1,'a','b','c','d'}
print(len(s1))
s1={
1,'a','b','c','d'}
print("c" in s1) #True
print("c" not in s1) #False

3. Value cycle

• Sets are unordered , So use for The values taken out of the loop are also out of order

s1={
1,'a','b','c','d'}
for i in s1:
print(i)
# d
# 1
# c
# b
# a

Operations that need to be mastered (****)

1. to update .update( )

• New set updates old set , If there is one, don't add , If nothing, add
• You can add more than one value at a time

s1={
'a','b','c'}
s1.update({
"a",3,4,5})
print(s1) # {'a','b','c',3,4,5}

2. add to .add( )

• Only one value can be added at a time

s1={
'a','b','c'}
s1.add(4)
print(s1) #{'c', 'b', 'a', 4}

3. Take a value .pop( )

• Do not specify parameters , Randomly delete any element in the set , And return this value

s={
"aaa",22,3,"bbb"}
res=s.pop()
print(s) #{3, 'aaa', 22}
print(res) #bbb

4. Delete .remove( ), .discard( )

• .remove( ) : When the deleted element does not exist , Report errors
• .discard( ) : When the deleted element does not exist , Don't complain

s1={
'a','b','c'}
# "remove" Delete 
s1.remove(4) # Report errors 
# "discard" Delete 
s1.discard(4) # Don't complain 

5. No intersection .isdisjoint( )

• If two sets do not have any intersection, return True

# No intersection experiment 
s1={
1,2,3}
s2={
4,5,6}
print(s1.isdisjoint(s2)) #T
print(s2.isdisjoint(s1)) #T
# There's an intersection experiment 
s1={
1,2,3}
s2={
4,5,6,3}
print(s1.isdisjoint(s2)) #T
print(s2.isdisjoint(s1)) #T

Operations that don't need to know much (***)

1…difference_update( )

2…intersection_ update( )

3…symmetric_ difference_ update( )

6、 ... and . summary

• You can store multiple values

• disorder

• Variable type —> must not hash type

ps : The values in the set must be immutable

print(s1.isdisjoint(s2)) #T
print(s2.isdisjoint(s1)) #T

## Operations that don't need to know much (***)
### 1..difference_update( )
### 2..intersection_ update( )
### 3..symmetric_ difference_ update( )
## 6、 ... and . summary
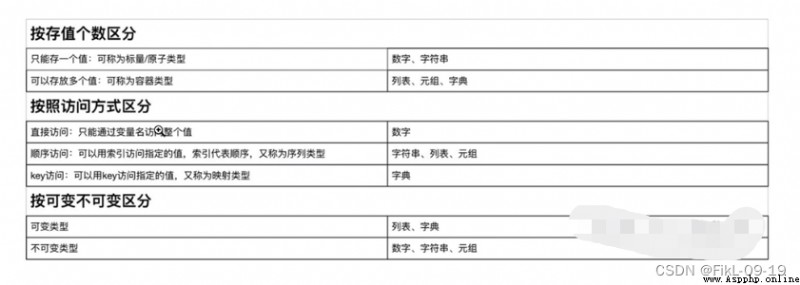
- ### You can store multiple values
- #### disorder
- #### Variable type ---> must not hash type
[ Outside the chain picture transfer in ...(img-2rHa53oA-1656084132890)]
ps : The values in the set must be immutable