Keep creating , Accelerate growth ! This is my participation 「 Nuggets day new plan · 6 Yuegengwen challenge 」 Of the 33 God , Click to see the event details
You are given the root of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return the minimum number of cameras needed to monitor all nodes of the tree.
Example 1:
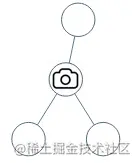
Input: root = [0,0,null,0,0]
Output: 1
Explanation: One camera is enough to monitor all nodes if placed as shown.
Example 2:
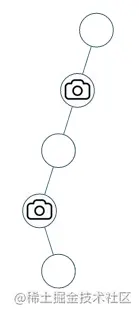
Input: root = [0,0,null,0,null,0,null,null,0]
Output: 2
Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
Note:
The number of nodes in the tree is in the range [1, 1000].
Node.val == 0
According to the meaning , Given the root of a binary tree root . We install cameras on tree nodes , Each camera on a node can monitor its parent node 、 Itself and its immediate child nodes . Returns the minimum number of cameras required to monitor all nodes of the tree .
Remember a little , Encountered the problem of binary tree , Let's solve the problem in the form of recursion . This problem also hides the greedy thought , Let's first define three states :
These three states contain all the situations in the binary tree , According to the idea of greed , We try to make the parent node install cameras from bottom to top , Because this way the camera can cover a wider range , We will also use the least number of cameras . The specific recursive solution ideas are all in the notes , Combined with the code, it will be clear at a glance .
The time complexity is O(N) , The space complexity is O(K) ,K Is the depth of the tree , That is, the depth of the recursive stack .
class Solution(object):
def __init__(self):
self.result = 0
def minCameraCover(self, root):
if not root.left and not root.right: return 1
def dfs(node):
if not node: return 2
L = dfs(node.left)
R = dfs(node.right)
# If both the left subtree and the right subtree are covered by the camera , Then the current node does nothing , Wait for its parent node to install the camera , This will reduce the number of cameras installed
if L == 2 and R == 2:
return 0
# At least one node is not covered , The current node needs to install a camera
elif L == 0 or R == 0:
self.result += 1
return 1
# If there is a left subtree or a subtree with a camera , The current node is covered by the camera , So there is no need to install a camera
elif L == 1 or R == 1:
return 2
if dfs(root) == 0:
self.result += 1
return self.result
Runtime: 27 ms, faster than 91.23% of Python online submissions for Binary Tree Cameras.
Memory Usage: 14 MB, less than 22.81% of Python online submissions for Binary Tree Cameras.
leetcode.com/problems/bi…
Your support is my greatest motivation