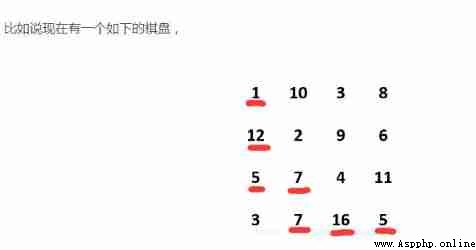
subject : In a m*n There is a gift in every space of the chessboard , Every gift has a certain value ( Value greater than
0). You can learn from the top left corner Start taking the gifts in the box , And move right or down one space at a time 、 Until you get to the end of the board The lower right corner . Given the value of a chessboard and its gifts , Please count your maximum / How much less valuable gifts can you get ?
Ideas : Dynamic programming .
Backward analysis , There is one i*j Matrix , The last step , Want to get to (i,j), Or from (i-1,j), Or from (i , j-1). The problems encountered at each step are the same , It's just a different way , Get different values .
f(i,j)=max(f(i,j-1)+f(i-1,j))+g(i,j) g(i,j) Indicates that the coordinates are (i,j) The value of gifts in the box
Recursive solution , There will be a lot of double counting , Through recursive analysis , Use a bottom-up loop to solve ( This topic is analyzed backwards , Direct solution )
The push process is as follows :
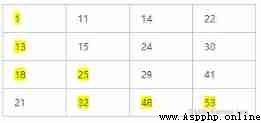
Intermediate results can be directly saved to the original array .
for loop , Next line per loop / Column , Calculate the sum of each position , Maximum / Minimum value use max/min Judge .
Code :
class Solution:
def func(self , array):
if len(array) <= 0 or array is None:
return 0
rows = len(array)
cols = len(array[0])
for i in range(rows):
for j in range(cols):
if i == 0 and j == 0:
continue
if i == 0:
array[i][j] += array[i][j -1]
elif j == 0:
array[i][j] += array[i -1][j]
else:
array[i][j] += max(array[i -1][j] , array[i][j-1]) # The greatest value , Minimum replacement min that will do
return array[rows-1][cols-1]
a = [[1,10,3,8] , [12,2,9,6] , [5,7,4,11] , [3,7,16,5]]
s = Solution()
print(s.func(a))