1、A/B test是什麼
A / B測試(也稱為分割測試或桶測試)是一種將網頁或應用程序的兩個版本相互比較以確定哪個版本的性能更好的方法。AB測試本質上是一個實驗,其中頁面的兩個或多個變體隨機顯示給用戶,統計分析確定哪個變體對於給定的轉換目標(指標如CTR)效果更好。
在本文中,我們將介紹分析 A/B 實驗的過程,從提出假設、測試到最終解釋結果。對於我們的數據,我們將使用來自 Kaggle 的數據集,其中包含對似乎是網站頁面的 2 種不同設計(old_page 與 new_page)的 A/B 測試的結果。
這是我們要做的:
1,設計我們的實驗
(選定指標,建立假設,選擇實驗單比特,計算樣本量,流量分割,實驗周期計算,線上驗證策略是否已實施)
2,收集和准備數據
3,可視化結果
4,檢驗假設
5,得出結論
為了使它更現實一點,這裏有一個我們研究的潛在場景
假設您在一家中型在線電子商務企業的產品團隊工作。UI 設計師在新版本的產品頁面上非常努力,希望它能帶來更高的轉化率。產品經理(PM)告訴你,目前的轉化率全年平均在13%左右,如果提高2% ,團隊會很高興,也就是說,新設計如果提高了,就被認為是成功的。轉化率15%。
在推出更改之前,團隊會更願意在少數用戶上對其進行測試以了解其性能,因此您建議對一部分用戶群用戶進行A/B 測試。
設計我們的實驗
選定我們的指標,相對值指標:轉化率。
選實驗單比特:用戶粒度,一個user_id作為唯一標識
提出假設:
鑒於我們不知道新設計的性能是否會與我們當前的設計更好或更差(或相同?),我們將選擇雙尾實驗:
Hₒ:p = p ₒ
Hₐ :p ≠ pₒ
其中p和p ₒ分別代錶新舊設計的轉化率。我們還將設置95% 的置信水平:
α = 0.05
α值是我們設置的閾值,我們說“如果觀察到極端或更多結果的概率(p值)低於α,那麼我們拒絕 Null 假設”。由於我們的α=0.05(錶示概率為 5%),我們的置信度 (1- α ) 為 95%。
如果您不熟悉上述內容,請不要擔心,這實際上意味著無論我們在測試中觀察到新設計的轉化率如何,我們都希望有 95% 的把握它與我們舊設計的轉化率在統計上有所不同設計,在我們決定拒絕零假設 Hₒ 之前。
選擇樣本量
重要的是要注意,由於我們不會測試整個用戶群(我們的人口),我們將獲得的轉化率不可避免地只是對真實轉化率的估計。
我們決定在每個組中捕獲的人數(或用戶會話)將影響我們估計的轉化率的精度: 樣本量越大,我們的估計越精確(即我們的置信區間越小),發現差異的機會越高在兩組中,如果存在的話。
另一方面,我們的樣本數越大,我們的研究就越昂貴(和不切實際),通常來說都是選擇最低滿足的樣本數。
那麼我們每個組應該有多少人呢?
我們需要的樣本量是通過一種叫做Power analysis的東西來估計的,它取決於幾個因素:
檢驗的功效(1 - β) — 這錶示當實際存在差異時,在我們的檢驗中發現組之間的統計差異的概率。按照慣例,這通常設置為 0.8
Alpha 值(α) — 我們之前設置為 0.05 的臨界值
效果大小——我們預計轉化率之間的差異有多大
由於我們的團隊會對 2% 的差異感到滿意,因此我們可以使用 13% 和 15% 來計算我們預期的效果大小。
Python 為我們處理了所有這些計算:
# 包導入
import numpy as np
import pandas as pd
import scipy.stats as stats
import statsmodels.stats.api as sms
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
from math import ceil
%matplotlib inline
# 一些繪圖樣式偏好
plt.style.use('seaborn-whitegrid')
font = {
'family' : 'Helvetica',
'weight' : 'bold',
'size' : 14}
mpl.rc('font', **font)
effect_size = sms.proportion_effectsize(0.13, 0.15) # 根據我們的預期比率計算效果大小
required_n = sms.NormalIndPower().solve_power(
effect_size,
power=0.8,
alpha=0.05,
ratio=1
) # 計算所需樣本量
required_n = ceil(required_n) # 四捨五入到下一個整數
print(required_n)
輸出:4720
在實踐中將power參數設置為 0.8 意味著如果我們的設計之間的轉化率存在實際差異,假設差異是我們估計的差異(13% 對 15%),我們有大約 80% 的機會將其檢測為在我們計算的樣本量的測試中具有統計學意義。
當然,你也可以用:
這個近似公式進行評估樣本量
按照絕對值指標赫相對值指標去定義,標准差值計算會有所不同:
開始查看我們的數據:
df = pd.read_csv('ab_data.csv')
df.head()
輸出:
df.info()
輸出:
DataFrame 中有294478 行,每行代錶一個用戶會話,以及5 列:
user_id- 每個會話的用戶 ID
timestamp- 會話的時間戳
group- 用戶被分配到該會話的哪個組 { control組, treatment組}
landing_page- 每個用戶在該會話中看到的設計 { old_page(老頁面), new_page}(新頁面)
converted- 會話是否轉化(0=未轉化,1=轉化)
我們實際上只會使用group和converted列進行分析。
在我們繼續對數據進行采樣以獲得我們的子集之前,讓我們確保沒有用戶被多次采樣。
有 3894 個用戶出現了不止一次。由於數量非常少,我們將繼續將它們從 DataFrame 中刪除,以避免對相同的用戶進行兩次采樣。
sers_to_drop = session_counts[session_counts > 1].index
df = df[~df['user_id'].isin(users_to_drop)]
print(f'更新的數據集現在有{
df.shape[0]}個條目')
采樣
現在我們的 DataFrame 幹淨整潔,我們可以繼續並n=4720為每個組采樣條目。我們可以使用 pandas 的DataFrame.sample()方法來執行此操作,它將為我們執行簡單隨機抽樣。
注意random_state=22:如果您想在自己的筆記本上進行操作,我已設置為可重現結果:只需random_state=22在您的函數中使用,您應該得到與我相同的示例。
control_sample = df[df['group'] == 'control'].sample(n=required_n, random_state=22)
treatment_sample = df[df['group'] == 'treatment'].sample(n=required_n, random_state=22)
ab_test = pd.concat([control_sample, treatment_sample], axis=0)
ab_test.reset_index(drop=True, inplace=True)
ab_test
ab_test.info()

看看實驗組和對照組的分割情況
ab_test['group'].value_counts()

很棒!
3. 可視化結果
conversion_rates = ab_test.groupby('group')['converted']
std_p = lambda x: np.std(x, ddof=0) # Std. 比例偏差
se_p = lambda x: stats.sem(x, ddof=0) # Std. 比例誤差 (std / sqrt(n))
conversion_rates = conversion_rates.agg([np.mean, std_p, se_p])
conversion_rates.columns = ['conversion_rate', 'std_deviation', 'std_error']
conversion_rates.style.format ('{:.3f}')

從上面的統計數據來看,看起來我們的兩個設計的錶現非常相似,我們的新設計錶現得稍微好一些,大約。12.3% 對 12.6% 的轉化率。
可視化代碼:
plt.figure(figsize=(8,6))
sns.barplot(x=ab_test['group'], y=ab_test['converted'], ci=False)
plt.ylim(0, 0.17)
plt.title( '按組的轉化率', pad=20)
plt.xlabel('Group', labelpad=15)
plt.ylabel('Converted (proportion)', labelpad=15);
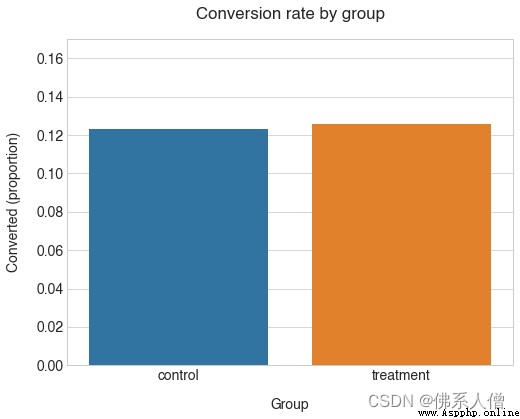
我們組的轉化率確實非常接近。另請注意,control考慮到我們對平均值的了解,該組的轉化率低於我們的預期。轉化率(12.3% 對 13%)。這錶明從總體中抽樣時結果存在一些差異。
所以treatment團體的價值更高。這種差異在統計學上是否顯著?
4. 檢驗假設
我們分析的最後一步是檢驗我們的假設。由於我們有一個非常大的樣本,我們可以使用正態近似來計算我們的p值(即 z 檢驗)。
同樣,Python 使所有計算變得非常容易。我們可以使用該statsmodels.stats.proportion模塊來獲取p值和置信區間:
from statsmodels.stats.proportion import ratios_ztest, ratio_confint
control_results = ab_test[ab_test['group'] == 'control']['converted']
treatment_results = ab_test[ab_test['group'] == 'treatment']['converted']
n_con = control_results.count()
n_treat = treatment_results.count()
成功 = [control_results.sum(),treatment_results.sum()]
nobs = [n_con, n_treat]
z_stat, pval = ratios_ztest(successes, nobs=nobs)
(lower_con , lower_treat), (upper_con, upper_treat) = ratio_confint(successes, nobs=nobs, alpha=0.05)
print(f'z statistic: {
z_stat:.2f}')
print(f'p-value: {
pval:.3f }')
print(f'ci 95% for control group: [{
lower_con:.3f}, {
upper_con:.3f}]')
print(f'ci 95% for treatment group: [{
lower_treat:.3f}, {
upper_treat:.3f}]')

5. 得出結論
由於我們的p -value=0.732 遠高於我們的 α=0.05閾值,我們不能拒絕零假設 Hₒ,這意味著我們的新設計與舊設計相比並沒有顯著不同(更不用說更好了)
此外,如果我們查看該treatment組的置信區間([0.116, 0.135] 或 11.6-13.5%),我們會注意到:
它包括我們 13% 轉化率的基准值
它不包括我們 15% 的目標值(我們的目標是 2% 的提昇)
這意味著新設計的真實轉化率更有可能與我們的基線相似,而不是我們希望的 15% 的目標。這進一步證明了我們的新設計不太可能是對舊設計的改進。