This module standardizes a set of fast , The core set of memory efficient tools , These tools are useful by themselves or in combination . Together they form a “ Iterator algebra ”, Thus, in pure Python Build specialized tools succinctly and efficiently in .
itertools Introduction to the module's official website
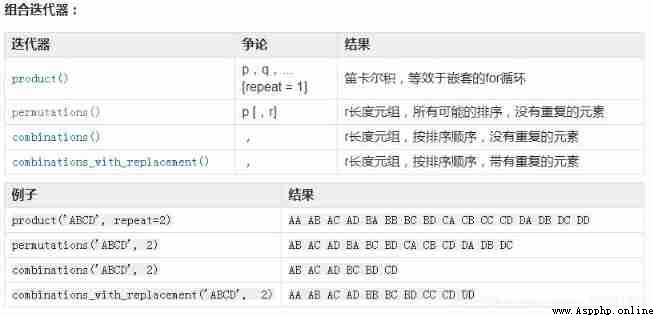
Enter the Cartesian product of the iteratable term
Roughly equivalent to nesting in generator expressions for loop . for example , Returns the same result as .product(A, B)((x,y) for x in A for y in B)
Nested loops loop like an odometer , The rightmost element advances in each iteration . This mode creates a dictionary order , So that if the input iteratable objects are sorted , Product tuples will be issued in sorted order .
itertools.product(* iterables,repeat = 1 )
give an example :
product('ABCD', repeat=2)
#AA AB AC AD BA BB BC BD CA CB CC CD DA DB DC DD
Equivalent code :
This function is roughly equivalent to the following code , The difference is that the actual implementation does not create intermediate results in memory :
def product(*args, repeat=1):
# product('ABCD', 'xy') --> Ax Ay Bx By Cx Cy Dx Dy
# product(range(2), repeat=3) --> 000 001 010 011 100 101 110 111
pools = [tuple(pool) for pool in args] * repeat
result = [[]]
for pool in pools:
result = [x+[y] for x in result for y in pool]
for prod in result:
yield tuple(prod)
return iterable Continuity of elements in r Length arrangement .
itertools.permutations(iterable, r=None)
give an example :
permutations('ABCD', 2)
#AB AC AD BA BC BD CA CB CD DA DB DC
Internal code implementation
def permutations(iterable, r=None):
# permutations('ABCD', 2) --> AB AC AD BA BC BD CA CB CD DA DB DC
# permutations(range(3)) --> 012 021 102 120 201 210
pool = tuple(iterable)
n = len(pool)
r = n if r is None else r
if r > n:
return
indices = list(range(n))
cycles = list(range(n, n-r, -1))
yield tuple(pool[i] for i in indices[:r])
while n:
for i in reversed(range(r)):
cycles[i] -= 1
if cycles[i] == 0:
indices[i:] = indices[i+1:] + indices[i:i+1]
cycles[i] = n - i
else:
j = cycles[i]
indices[i], indices[-j] = indices[-j], indices[i]
yield tuple(pool[i] for i in indices[:r])
break
else:
return
itertools.combinations(iterable, r)
r Length tuple , By sort order , There are no repeating elements
give an example :
combinations('ABCD', 2)
#AB AC AD BC BD CD
According to input iterable The order of , Emit combined tuples in dictionary order . therefore , If the input iterable Sort , The combined tuple will be generated in the sort order .
Elements are considered unique according to their location rather than their value . therefore , If the input element is unique , Then there will be no duplicate values in each combination .
amount to
def combinations(iterable, r):
# combinations('ABCD', 2) --> AB AC AD BC BD CD
# combinations(range(4), 3) --> 012 013 023 123
pool = tuple(iterable)
n = len(pool)
if r > n:
return
indices = list(range(r))
yield tuple(pool[i] for i in indices)
while True:
for i in reversed(range(r)):
if indices[i] != i + n - r:
break
else:
return
indices[i] += 1
for j in range(i+1, r):
indices[j] = indices[j-1] + 1
yield tuple(pool[i] for i in indices)
Code for combinations() It can also be expressed as permutations() Element filtered subsequence , Where the elements are not in order ( According to their position in the input pool ):
def combinations(iterable, r):
pool = tuple(iterable)
n = len(pool)
for indices in permutations(range(n), r):
if sorted(indices) == list(indices):
yield tuple(pool[i] for i in indices)
Enter the... Of the iteratively returned element r Length subsequence , Allow a single element to repeat multiple times .
itertools.combinations_with_replacement(iterable, r)
give an example :
combinations_with_replacement('ABCD', 2)
#AA AB AC AD BB BC BD CC CD DD
According to input iterable The order of , Emit combined tuples in dictionary order . therefore , If the input iterable Sort , The combined tuple will be generated in the sort order .
Elements are considered unique according to their location rather than their value . therefore , If the input element is unique , The generated combination will also be unique .
Roughly equivalent to :
def combinations_with_replacement(iterable, r):
# combinations_with_replacement('ABC', 2) --> AA AB AC BB BC CC
pool = tuple(iterable)
n = len(pool)
if not n and r:
return
indices = [0] * r
yield tuple(pool[i] for i in indices)
while True:
for i in reversed(range(r)):
if indices[i] != n - 1:
break
else:
return
indices[i:] = [indices[i] + 1] * (r - i)
yield tuple(pool[i] for i in indices)
Code for combinations_with_replacement() It can also be expressed as product() Element filtered subsequence , Where the elements are not in order ( According to their position in the input pool ):
def combinations_with_replacement(iterable, r):
pool = tuple(iterable)
n = len(pool)
for indices in product(range(n), repeat=r):
if sorted(indices) == list(indices):
yield tuple(pool[i] for i in indices)
The number of items returned .(n+r-1)! / r! / (n-1)!n > 0
Problem description : give 4 individual 1-10 The number of , By addition, subtraction, multiplication and division , Get the number as 24 Even if we win
import sys
import itertools
def func(cards):
for nums in itertools.permutations(cards): # Four numbers
for ops in itertools.product('+-*/', repeat=3): # Three operators ( repeatable !)
# Construct three infix expressions (bsd)
bds1 = '({0}{4}{1}){5}({2}{6}{3})'.format(*nums, *ops) # (a+b)*(c-d)
bds2 = '(({0}{4}{1}){5}{2}){6}{3}'.format(*nums, *ops) # (a+b)*c-d
bds3 = '{0}{4}({1}{5}({2}{6}{3}))'.format(*nums, *ops) # a/(b-(c/d))
for bds in [bds1, bds2, bds3]: # Traverse
try:
if abs(eval(bds) - 24.0) < 1e-10: # eval function
return 'true'
except ZeroDivisionError: # Zero division error !
continue
return 'false'
for line in sys.stdin:
nums = list(map(int, line.strip().split()))
print(str(func(nums)).lower())