遞歸,從原理上講,就是 函數直接或間接地調用自身的算法 。是重復調用函數自身實現循環,遇到滿足終止條件的情況時逐層返回結束循環,是一種算法結構。
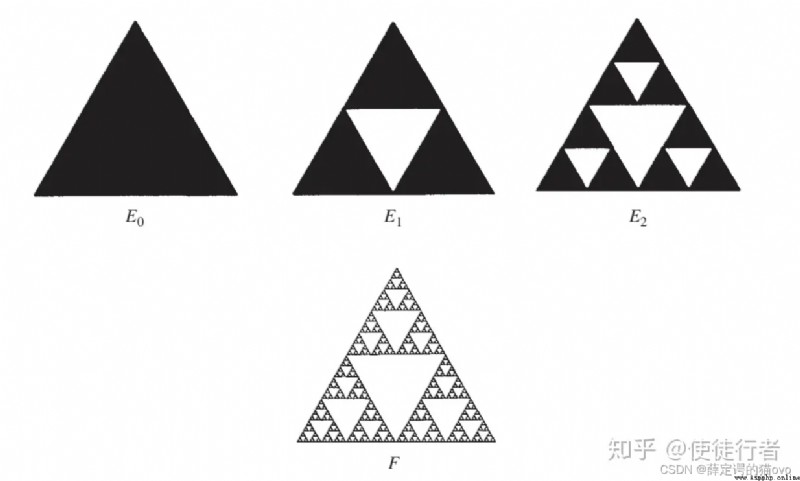
遞歸在日常編程中有很多例子,例如謝爾賓斯基三角形:
正整數的階乘是指從1乘以2乘以3乘以4一直盛到所要求的的數。例如,所要求的數是5的階乘,則階乘式是1×2×3×4×5,得到的積是120,所以120就是5的階乘。
非遞歸版本:
# 計算階乘(非遞歸)def recrusion(n): result = n for i in range(1, n): result *= i return resultnumber = int(input('請輸入一個整數:'))result = recrusion(number)print("%d 的階乘是:%d" % (number, result))其執行結果如下:

遞歸版本:
# 計算階乘(遞歸)def recrusion(n): if n == 1: return 1 else: return n*recrusion(n-1)number = int(input('請輸入一個整數:'))result = recrusion(number)print("%d 的階乘是:%d" % (number, result))其執行結果為:

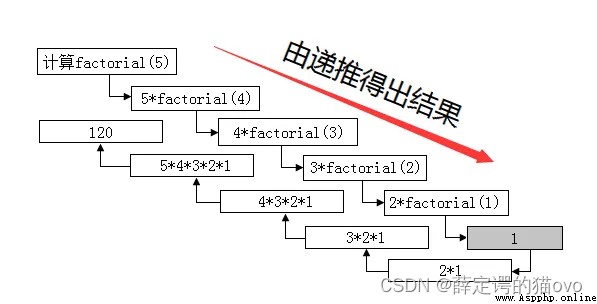
遞歸函數的實現詳細分析如下圖所示:
這個例子滿足了 遞歸的兩個條件 :
(1)調用函數本身
(2)設置了正確的返回條件
再介紹一個遞歸的經典例題——斐波那契數列。斐波那契數列的發明者,是意大利數學家列昂納多·斐波那契(Leonardo Fibonacci)。其大致描述是這樣的:
假如有一對剛出生的小兔子,只需要一個月小兔子就能長成大兔子,從第三個月開始,這對大兔子每個月都會生下一對小兔子。新出生的小兔子又會花一個月長大,再花一個月開始生兔子…也就是說,兔子在出生兩個月後,就有繁殖能力,在擁有繁殖能力後,這對兔子每個月能生出一對小兔子來, 如果每對兔子都經歷這樣的出生、成熟、生育的過程,並且永遠不死,那麼每個月兔子的總數是多少呢?
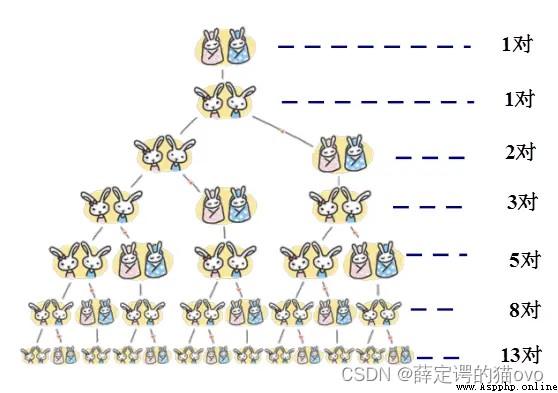
第一個月只有1對兔寶寶。
第二個月只有1對大兔子。
第三個月大兔子生了一對兔寶寶,一大一小2對兔子。
第四個月大兔子繼續生一對兔寶寶,小兔子變成大兔子。兩大一小3對兔子。
….
於是,我們可以得到每個月兔子的總數:
可以用數學函數來定義:
遞歸實現:
# 實現斐波那契數列def fab(n): if n < 1: print('輸入有誤!') return -1 if n == 1 or n == 2: return 1 else: return fab(n-1) + fab(n-2)result = fab(12)if result != -1: print("第12個月共有%d對兔子" % result) 其執行結果為144。
遞歸的邏輯很簡單,但是 遞歸如果使用不當,效率會很低 。因為遞歸的實現是函數自己調用自身,每次函數的調用都需要進行壓棧、出棧、保存和恢復寄存器的操作,所以在這上邊是非常消耗時間和空間的。
法國數學家愛德華·盧卡斯曾編寫過一個印度的古老傳說:在世界中心貝拿勒斯(在印度北部)的聖廟裡,一塊黃銅板上插著三根寶石針。印度教的主神梵天在創造世界的時候,在其中一根針上從下到上地穿好了由大到小的64片金片,這就是所謂的漢諾塔。不論白天黑夜,總有一個僧侶在按照下面的法則移動這些金片:一次只移動一片,不管在哪根針上,小片必須在大片上面。僧侶們預言,當所有的金片都從梵天穿好的那根針上移到另外一根針上時,世界就將在一聲霹雳中消滅,而梵塔、廟宇和眾生也都將同歸於盡。
要解決這個問題,其思路如下:
(1)將前63個盤子從A移動到B上,確保大盤在小盤底下。
(2)將最底下的第64個盤子從A移動到C上。
(3)將B上的63個盤子移動到C上。
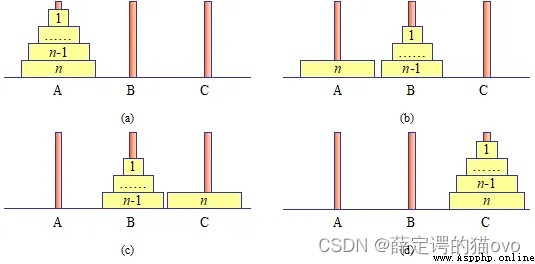
解決問題的思路有了,關鍵在於步驟(1)和步驟(3)如何執行。由於每次只能移動一個圓盤,所以在移動過程中,顯然要借助另外一根針才可以實施。也就是說, 步驟(1)將1~63個盤子需要借助C移到B上 , 步驟(3)將B上的63個盤子借助A移動到C上 。
所以,把新的思路聚集為以下兩個問題:
問題一:將A上的63個盤子借助C移動到B上;
問題二:將B上的63個盤子借助A移動到C上。
而相應的 問題一和問題二的解決方法跟剛才第一個問題的思路是一樣的 。
問題一(將A上的63個盤子借助C移動到B上)可拆解為:
(1)將前62個盤子從A移動到C上,確保大盤在小盤下。
(2)將最底下的第63個盤子移動到B上。
(3)將C上的62個盤子移動到B上。
問題二(將B上的63個盤子借助A移動到C上)可拆解為:
(1)將前62個盤子從B移動到A上,確保大盤在小盤下。
(2)將最底下的第63個盤子移動到C上。
(3)將A上的62個盤子移動到C上。
所以,這個難題可以用遞歸來解決:
# 漢諾塔問題def hanoi(n, a, b, c): # 將第n層從a借助b移動到c if n == 1: print(a, '-->', c) # 如果只有一層,直接從a移動到c else: hanoi(n-1, a, c, b) # 將前n-1個盤子從a移動到b上 print(a, '-->', c) # 將最底下的第64個盤子從a移動到c上 hanoi(n-1, b, a ,c) # 將b上的63個盤子移動到c上n = int(input('請輸入漢諾塔的層數:'))hanoi(n, 'A', 'B', 'C')作者:薛定谔的貓ovo
游戲編程,一個游戲開發收藏夾~
如果圖片長時間未顯示,請使用Chrome內核浏覽器。