大家好,最近實在是有點忙,下篇遲遲沒有動筆。上一篇文章也結束得很匆忙,實在抱歉。代碼部分其實早已寫好,但是問哥還是想盡力將其拆解、講解清楚,所以並不是直接分享代碼。當然,如果想跳過問哥啰嗦的廢話,直接參考代碼,也可以跳到文章末尾查閱。
廢話不多說,馬上進入我們剩下的部分:
上篇 —— 游戲界面搭建
下篇 —— 功能代碼實現
游戲規則比較簡單:找一副撲克牌,去掉大小王,52張牌,每次隨機抽取四張牌,運用加減乘除四種計算方法,看看誰能最快計算出24點。雖說是單機游戲,沒有比賽的壓力,但還是增加了計時功能:如果90秒內未能找出答案,則視為當前測試失敗,自動進入下一關。同時,為了降低難度,提供了提示功能:闖關過程中,共有三次機會獲得提示參考答案。
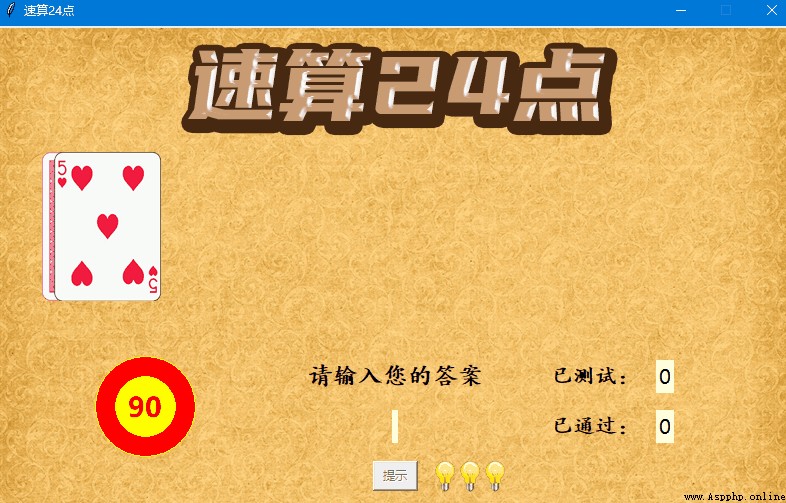
游戲截圖:

速算24點的簡易流程圖如下:
上篇內容裡講解了大部分界面的搭建,還有兩個小地方,一個是關卡信息,一個是提示按鈕。
上篇我們引入了StringVar類,實例了變量後,用來和標簽綁定,可以直接將變量的內容顯示在標簽上,從而省去了不少麻煩。而StringVar是針對字符串,對於純粹的數字,tkinter還提供了類似功能的IntVar類。同樣地,將其和標簽或其他組件綁定,即可直接將IntVar類實例的值顯示出來。與StringVar相區別的是,IntVar是整數(int),可以直接參與計算,所以,用來記錄玩家已測試的關卡數,以及通過的關卡(分數),也是十分方便的。
於是,我們先定義兩個變量,實例化IntVar類:
level=IntVar()score=IntVar()再創建4個標簽,兩個用來顯示固定字符“已測試”、“已通過”,另外兩個用來和變量level、score綁定,以動態顯示當前的關卡和分數。
cv.create_text(600,350,text='已測試:',font =('方正楷體簡體',16,'bold'))cv.create_text(600,400,text='已通過:',font =('方正楷體簡體',16,'bold'))level_lable = Label(root,text='',font=('微軟雅黑',15),textvariable=level,bg='lightyellow')cv_level = cv.create_window(670,350,window=level_lable)score_lable = Label(root,text='',font=('微軟雅黑',15),textvariable=score,bg='lightyellow')cv_score = cv.create_window(670,400,window=score_lable)實現效果如下圖:

提示按鈕區域還分了兩部分,一部分是按鈕,另一部分是小燈泡的圖片,用來表示玩家還剩多少次機會。
問哥從網上找到的小燈泡的圖片,將它改成png格式,然後命名為idea。

先定義一個常量HINT,用來表示玩家可以有多少次提示機會。默認是3次,當然你也可以改成5次,更多或更少。然後再通過for循環,在指定的位置繪制3個燈泡圖片,並將這些繪制的組件放在一個列表ideas裡。
HINT = 3idea = PhotoImage(file=r"image\poker\idea.png")ideas = []for i in range(HINT): ideas.append(cv.create_image(450+i*25,450,image = idea))為什麼放進列表呢?因為可以方便我們在按下提示按鈕後,自動減少圖片並在畫布上刷新。
按鈕的創建很簡單,我們之前也介紹過。問哥為了加速完成這個小項目,就不使用特效了,於是默認使用tkinter的Button組件。
btn = Button(root,text='提示',width=5,command=hint)cv_btn = cv.create_window(400,450,window=btn)關鍵是我們需要為這個按鈕綁定一個回調函數,起名叫hint,在該函數裡,我們要完成以下三個功能:
將按鈕禁用,以防止玩家不小心點擊了多次,從而浪費了提示次數
減少一個“小燈泡” 實現代碼如下:
def hint(): answer.set(right_answer) btn['state']=DISABLED idea = ideas.pop() cv.delete(idea) 同樣的道理,為了防止玩家誤操作(你永遠無法完全預見玩家或用戶大開腦洞的操作),也為了減少程序的可能,我們規定該按鈕只允許在被點擊的時候啟用,換句話說,除了倒計時開始,玩家開始答題時,而且提示次數沒有用完(ideas>0),按鈕的狀態是NORMAL,其他時間該按鈕都應該處於DISABLED狀態。
於是,我們分別在其他位置做以下更新:
def initialize(): # 省略代碼 btn['state']=DISABLEDdef draw_card(): # 省略代碼 if len(ideas)>0: btn['state']=NORMAL測試效果基本OK:

代碼寫到這裡,除了還沒有讓電腦替我們找出正確答案,已經實現基本的輸入、判斷等功能了。試著運行一下:
發現回答正確、在選擇繼續下一局後,桌面上的發牌混亂了,不知道新的四張牌跑到哪裡去了,這是怎麼回事?
原來,我們在上篇用了一個數組cv_card來儲存抽出來的四張牌,並使用for循環將這四張牌顯示在桌面上,但是沒有考慮到當一局游戲結束,需要重新抽四張牌的情況。在這種情況下,我們需要把桌面上的4張牌從畫布上擦去,用代碼的話主要是兩步:
清空列表 為了避免重復操作,我們再定義一個子程序來完成清除clear的操作:
def clear(cv_card): for i in cv_card: cv.delete(i) cv_card.clear()然後,我們再把該函數放在抓牌函數的開始,這樣,每次開始抓牌前,我們都先清除(如果有的話)上一輪的四張牌,從而保證代碼對新的四張牌依然適用。
def draw_card(): clear(cv_card)同樣的理由,我們在重新開始下一局後,答案標簽的內容也需要清空,所以我們需要在initialize函數以及myanswer函數裡添加以下代碼:
def initialize(): answer.set('') # 省略代碼def myanswer(event): # 省略代碼 if s=='BackSpace': txt=txt[:-1] elif s=='Return': if is_right(txt): root.after_cancel(cd) c = tm.askyesno(message='繼續下一局嗎?') if c: # 省略代碼 return # 添加 return,表示進入下一局後就不繼續顯示標簽經測試,在沒有電腦幫助的情況下,已經可以成功地“自食其力”進行闖關了。可問題是,常常會出現這種情況:抽出四張牌,卻很難寫出答案,因為我們也無法確定是我們沒有想出答案,還是這四張牌根本沒有答案。所以,我們需要設計一個方法,讓電腦替我們先算好答案,保存在變量right_answer裡,如果沒有答案的話,就自動更換下一組。有了right_answer,提示按鈕也就可以發揮作用了。
算起來,這部分其實是相對獨立的代碼,因為我們可以把要解決的問題從這個游戲裡抽離出來,轉換為“給定4個數,計算出能否通過排列組合,使得這四個數組成的算式運算結果等於24。”
為了解決這個問題,我們觀察一下四個數字組成的算術表達式的特征:
考慮小括號的情況又分為兩種:
雖然存在很多重復計算,但在不考慮時間復雜度,以及運算量並不算大的情況下,完全可以讓電腦進行窮舉運算,把所有的可能性都檢查一遍。於是我們可以把代碼的實現過程分成三步:
找出3個運算符(加減乘除)的排列組合,因為運算符可重復使用,所以是4^3=64種可能。(這裡面有一些組合是不可能計算出24點的,比如連續三個減號或除號,但是如果添加小括號使得計算順序發生改變的話,結果將有所不同。為了省事,這裡就把所有排列組合都考慮了)
在算式的不同位置添加小括號。根據前面列舉的,總共有8種可能。 於是,不考慮存在重復的情況下,最多總共有 24*64*8 = 12288 種可能。這點計算量對人類來說可能望而卻步,但是對電腦來說簡直不值一提。更何況,我們並不用找出所有正確答案,而是只要找到一個即可。
下面我們開始寫代碼:
我們首先要做的,就是把抽取的4張牌轉化為數字。因為撲克牌的數字是從0到51,但是所代表的用於計算的數字卻是從1到13,這其實可以通過簡單的求余運算來實現。
於是,我們定義一個函數:
def calnum(n): global nums nums=[i%13+1 for i in n] formula=form(nums) 這個函數接收一個變量n,代表含有4張牌的列表,然後通過列表生成式(或稱為推導式)將其轉換成一個實際用於計算的數字的列表nums。然後再調用另一個自定義函數form()將這個列表通過排列組合轉化成含有最多12288個表達式的列表,保存為formula。
需要注意的是,我們還要將nums聲明成全局變量。這樣做的唯一目的,是為了在判斷玩家輸入的時候,是否只使用了給定的4個數字。於是,我們順便將判斷玩家輸入的函數 is_right() 也更新如下:
def is_right(txt): # 省略代碼 if sorted(txt)!=sorted(nums): tm.showinfo(message='請使用給定的數字!') return False # 省略代碼下面我們接著寫form()函數。
為了不重復制造輪子,我們可以直接使用Python提供的內置模塊來計算排列組合。
from itertools import permutationsdef form(nums): numlist=set(permutations(nums)) 從itertools模塊中導入permutations函數以後,就可以使用它來計算列表的排列組合了。這個函數接收兩個參數,第一個是列表等可迭代對象,第二個是數字,表示從前面的列表裡取出幾個元素進行排列組合,可以省略,如果省略的話,則表示默認對所有元素進行排列組合。於是在這裡,我們可以省略第二個參數,直接將含有4個數字的nums列表交給permutations函數,返回一個可迭代對象。同時,為了去重,比如四張牌裡有重復的數字,3,3,4,4這種,我們可以將這個結果轉換為集合set,最終將結果保存在numlist裡。
在控制台測試結果:
>>> from itertools import permutations>>> nums = [1,2,3,4]>>> numlist = permutations(nums)>>> type(numlist)<class 'itertools.permutations'>>>> for i in numlist: print(i,end=' ')(1, 2, 3, 4) (1, 2, 4, 3) (1, 3, 2, 4) (1, 3, 4, 2) (1, 4, 2, 3) (1, 4, 3, 2) (2, 1, 3, 4) (2, 1, 4, 3) (2, 3, 1, 4) (2, 3, 4, 1) (2, 4, 1, 3) (2, 4, 3, 1) (3, 1, 2, 4) (3, 1, 4, 2) (3, 2, 1, 4) (3, 2, 4, 1) (3, 4, 1, 2) (3, 4, 2, 1) (4, 1, 2, 3) (4, 1, 3, 2) (4, 2, 1, 3) (4, 2, 3, 1) (4, 3, 1, 2) (4, 3, 2, 1) >>> 可以看到,如我們所預想的,4個不重復的數字可以組成最多24個互不重復的組合。
接下來,我們需要在這四個數字中間插入三個運算符,當然,我們首先要找到運算符組成的64種組合,使用三層循環即可實現,並將結果保存在列表operations裡。
operations=[]for i in '+-*/': for j in '+-*/': for k in '+-*/': operation = i+j+k operations.append(operation) 因為這個列表會被頻繁調用(每發四張牌,就要插入運算符),所以我們可以將它放在主程序裡,這樣只要在游戲開始時運算一次,在函數裡就可以一直調用(而不修改)。
接著,在函數form裡,我們同樣使用for循環來將3個運算符插入到4個數字之間:
def form(nums): numlist=set(permutations(nums)) combo=[] for num in numlist: for i in operations: temp=[] for j in range(3): temp+=[str(num[j]),i[j]] temp.append(str(num[j+1])) combo.append(temp)因為最終我們需要將表達式轉換成字符串,所以在這裡我們就可以使用str函數將數字轉換成字符串,保存在列表combo裡。根據之前計算的,combo裡最多應該存在 24*64 = 1536 個元素,代表了1536個表達式。但是現在它們任然是單個的字符,因為我們還需要插入小括號。
小括號用於提升運算等級、改變運算順序。根據前面所分析的,由於默認計算順序為先乘除、後加減、從左到右依次運算,所以不包含小括號的情況(a+b+c+d)一定等價於某種使用小括號的情況。所以最終我們只需要考慮8種小括號的情況:三種一對小括號的情況,和五種兩對小括號的情況。但是該怎樣插入呢?
通過之前的計算,我們得到的combo二維列表裡的表達式列表應該類似這個樣子:
[‘1’, ‘+’, ‘2’, ‘+’, ‘3’, ‘+’, ‘4’]
可見,每個表達式都是包含7個字符串元素(4個數字、3個運算符)的列表。於是,我們只要事先找到需要添加小括號的位置(索引),就可以通過循環添加了。
通過比較,我們將兩種情況(一對和兩對小括號)的左右小括號的位置索引找到,並創建列表如下:
one=[(3,0),(5,2),(7,4)] two=[(7,3,5,0),(5,3,0,0),(5,5,2,0),(7,5,2,2),(7,7,4,2)] 需要注意的是,我們要先插入右邊的小括號,再插入左邊小括號。因為插入元素以後,列表的長度改變,為了方便計算,先插入右邊小括號可以最大程度保持相對位置。在兩對小括號的時候也是如此(先插入右側的括號),只需要注意其中一種情況:(a+b)+(c+d)。在這種情況下,插入兩個右括號之後,夾在兩個右括號中間的左括號位置發生了變化,只要記錄新的位置即可。
於是,通過索引列表,我們可以將form函數補全:
def form(nums): numlist=set(permutations(nums)) combo=[] for num in numlist: for i in operations: temp=[] for j in range(3): temp+=[str(num[j]),i[j]] temp.append(str(num[j+1])) combo.append(temp) one=[(3,0),(5,2),(7,4)] two=[(7,3,5,0),(5,3,0,0),(5,5,2,0),(7,5,2,2),(7,7,4,2)] formula=[] for i in combo: for j in one: temp=i[:] temp.insert(j[0],')') temp.insert(j[1],'(') formula.append(''.join(temp)) # 將列表轉化為字符串 for j in two: temp=i[:] temp.insert(j[0],')') temp.insert(j[1],')') temp.insert(j[2],'(') temp.insert(j[3],'(') formula.append(''.join(temp)) # 將列表轉化為字符串 return formula最後,我們得到包含最多12288個表達式的列表formula,並返回到函數calnum裡使用eval函數進行計算。
def calnum(n): # 省略代碼 formula=form(nums) for i in formula: try: result = eval(i) except: continue if math.isclose(result,24): return i return 'None'通過for循環遍歷formula列表,依次計算結果是否等於24。如果正確,則把正確答案(表達式)返回,如果遍歷所有12288種可能都沒有結果,則返回字符串None。
按照我們之前的邏輯,在每次抓取4張牌之後,我們都需要電腦幫忙計算,看看當前4張牌能否計算出24點,如果不能,則自動進入下一局(重新抓牌),如果可以,則將答案保存在變量right_answer裡,方便提示(hint)按鈕調用。於是,我們更新相應部位的代碼即可:
def draw_card(): global cv_card, right_answer invalid=True while invalid: clear(cv_card) draw=[] if len(cardnum)==0: tm.showinfo(message='牌堆已用完,為您重新洗牌') shuffle_card() for i in range(4): draw.append(cardnum.pop()) cv_card.append(cv.create_image(100,200,image=card[draw[i]])) if len(cardnum)==0:cv.delete(cv_back) for _ in range(150*(i+1)): cv.move(cv_card[i],1,0) cv.update() right_answer = calnum(draw) # 調用函數計算12288種可能 if right_answer=='None': tm.showinfo(message='本組數字無解,為您自動更換下一組') else: countdown() if len(ideas)>0: btn['state']=NORMAL invalid=False如果4張牌無法計算24點,就需要一直重新抽牌,直到可以計算為止。於是這裡使用一個while循環,並給定一個標記 invalid 假定當前組合無法計算24點。只有當得到答案時(right_answer的值不是None),invalid變為False,結束while循環,開始計時等後續程序。
IntVar類型
permutations函數 到這裡,我們這個“速算24點”的小游戲就做好了。大家可以繼續在裡面添加其他想要的功能,改變布局、顏色等等。最終運行效果如下:

from tkinter import *import tkinter.messagebox as tmimport randomimport mathfrom itertools import permutationsdef shuffle_card(): global cardnum, back, cv_back cardnum = list(range(52)) random.shuffle(cardnum) back = PhotoImage(file=r"image\poker\back1.png") cv_back = cv.create_image(100,200,image = back)def clear(cv_card): for i in cv_card: cv.delete(i) cv_card.clear()def draw_card(): global cv_card, right_answer invalid=True while invalid: clear(cv_card) draw=[] if len(cardnum)==0: tm.showinfo(message='牌堆已用完,為您重新洗牌') shuffle_card() for i in range(4): draw.append(cardnum.pop()) cv_card.append(cv.create_image(100,200,image=card[draw[i]])) if len(cardnum)==0:cv.delete(cv_back) for _ in range(150*(i+1)): cv.move(cv_card[i],1,0) cv.update() right_answer = calnum(draw) if right_answer=='None': tm.showinfo(message='本組數字無解,為您自動更換下一組') else: countdown() if len(ideas)>0: btn['state']=NORMAL invalid=Falsedef initialize(): global angle,count,cv_arc,cv_inner,cv_text count=90 angle=360 btn['state']=DISABLED answer.set('') cv_arc=cv.create_oval(100,330,200,430,fill='red',outline='yellow') cv_inner=cv.create_oval(120,350,180,410,fill='yellow',outline='yellow') cv_text=cv.create_text(150,380,text=count,font =('微軟雅黑',20,'bold'),fill='red') draw_card()def countdown(): global angle,count,cv_arc,cv_inner,cv_text,cd if angle == 360: angle -= 1 else: cv.delete(cv_arc) cv.delete(cv_inner) cv.delete(cv_text) cv_arc=cv.create_arc(100,330,200,430,start=90,extent=angle,fill="red",outline='yellow') angle -= 1 if angle%4 == 0: count-=1 cv_inner=cv.create_oval(120,350,180,410,fill='yellow',outline='yellow') cv_text=cv.create_text(150,380,text=count,font =('微軟雅黑',20,'bold'),fill='red') if count==0: tm.showinfo(message='倒計時結束!自動進入下一局') level.set(int(level.get())+1) cv.delete(cv_arc) cv.delete(cv_inner) cv.delete(cv_text) initialize() else: cd = root.after(250,countdown) def myanswer(event): s=event.keysym txt=answer.get() if s=='BackSpace': txt=txt[:-1] elif s=='Return': if is_right(txt): level.set(int(level.get())+1) score.set(int(score.get())+1) root.after_cancel(cd) c = tm.askyesno(message='繼續下一局嗎?') if c: cv.delete(cv_arc) cv.delete(cv_inner) cv.delete(cv_text) initialize() return else:root.destroy() else: txt='' elif s.isnumeric(): txt+=s elif s in trans: txt+=trans[s] answer.set(txt)def is_right(txt): try: result = eval(txt) except: tm.showinfo(message='算式不正確,請重新輸入!') return False for i in '+-*/()': txt=txt.replace(i,' ') txt=[int(i) for i in txt.split()] if sorted(txt)!=sorted(nums): tm.showinfo(message='請使用給定的數字!') return False if math.isclose(result,24): tm.showinfo(message='恭喜您!回答正確!') return Truedef hint(): answer.set(right_answer) btn['state']=DISABLED idea = ideas.pop() cv.delete(idea)def calnum(n): global nums nums=[i%13+1 for i in n] formula=form(nums) for i in formula: try: result = eval(i) except: continue if math.isclose(result,24): return i return 'None'def form(nums): numlist=set(permutations(nums)) combo=[] for num in numlist: for i in operations: temp=[] for j in range(3): temp+=[str(num[j]),i[j]] temp.append(str(num[j+1])) combo.append(temp) one=[(3,0),(5,2),(7,4)] two=[(7,3,5,0),(5,3,0,0),(5,5,2,0),(7,5,2,2),(7,7,4,2)] formula=[] for i in combo: for j in one: temp=i[:] temp.insert(j[0],')') temp.insert(j[1],'(') formula.append(''.join(temp)) for j in two: temp=i[:] temp.insert(j[0],')') temp.insert(j[1],')') temp.insert(j[2],'(') temp.insert(j[3],'(') formula.append(''.join(temp)) return formula# 游戲從這裡開始HINT = 3operations=[]for i in '+-*/': for j in '+-*/': for k in '+-*/': operation = i+j+k operations.append(operation)trans={'plus':'+','minus':'-','asterisk':'*','slash':'/','parenleft':'(','parenright':')'}root = Tk()root.geometry('800x500+400+200')root.resizable(0,0)root.title('速算24點')# 畫布大小和主窗口大小一致cv = Canvas(root,width=800,height=500)# 背景圖片bg = PhotoImage(file=r"image\poker\bg.png")cv_bg = cv.create_image(400,250,image = bg)# 標題圖片title = PhotoImage(file=r"image\poker\title.png")cv_title = cv.create_image(400,60,image = title)# 顯示答案及關卡分數等信息answer=StringVar()level=IntVar()score=IntVar()cv.create_text(400,350,text='請輸入您的答案',font =('方正楷體簡體',18,'bold'))lb = Label(root,text='',font=('微軟雅黑',15),textvariable=answer,bg='lightyellow')cv_lb = cv.create_window(400,400,window=lb)cv.create_text(600,350,text='已測試:',font =('方正楷體簡體',16,'bold'))cv.create_text(600,400,text='已通過:',font =('方正楷體簡體',16,'bold'))level_lable = Label(root,text='',font=('微軟雅黑',15),textvariable=level,bg='lightyellow')cv_level = cv.create_window(670,350,window=level_lable)score_lable = Label(root,text='',font=('微軟雅黑',15),textvariable=score,bg='lightyellow')cv_score = cv.create_window(670,400,window=score_lable)# 提示圖片及按鈕idea = PhotoImage(file=r"image\poker\idea.png")ideas = []for i in range(HINT): ideas.append(cv.create_image(450+i*25,450,image = idea))btn = Button(root,text='提示',width=5,command=hint)cv_btn = cv.create_window(400,450,window=btn)# 綁定從鍵盤獲取輸入<Key>,並傳給自定義函數myanswerlb.bind('<Key>',myanswer)# 使標簽組件獲得焦點,不然無法從鍵盤輸入lb.focus_set()card = [PhotoImage(file=f'image/poker/{i:0>2}.png') for i in range(1,53)]cv_card=[]cv.pack()shuffle_card()initialize()root.mainloop()作者:請叫我問哥
游戲編程,一個游戲開發收藏夾~
如果圖片長時間未顯示,請使用Chrome內核浏覽器。
 The front end (HTML) can receive the list data of the back end (Python view.py) render. How can the front end display a value of the list in a grid through a table?
The front end (HTML) can receive the list data of the back end (Python view.py) render. How can the front end display a value of the list in a grid through a table?
The phenomenon and background