Python foundation - recursion and its classic examples (factorial, Fibonacci sequence, Hanoi Tower)

What is recursion

recursive , In principle , Namely Functions directly or indirectly call their own algorithms . Is to repeatedly call the function itself to realize the loop , When the termination conditions are met, the end loop is returned layer by layer , Is an algorithm structure .
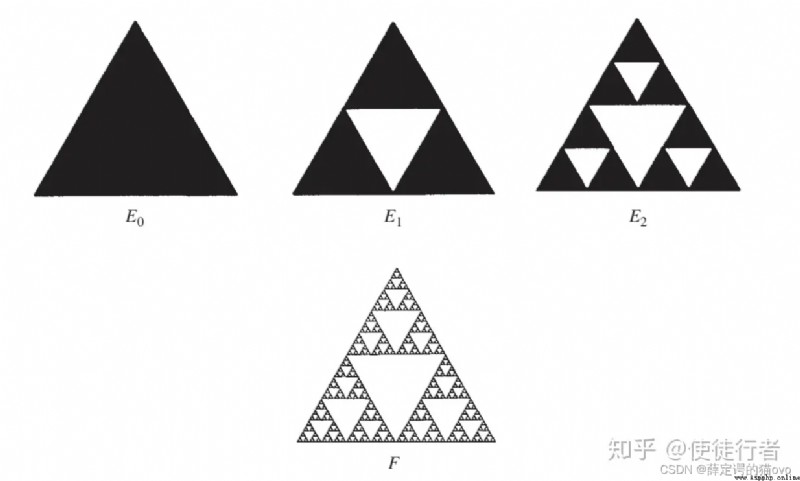
There are many examples of recursion in everyday programming , For example, the scherpinsky triangle ：

Factorial

The factorial of a positive integer is from 1 multiply 2 multiply 3 multiply 4 Until the required number . for example , The number required is 5 The factorial , Then the factorial is 1×2×3×4×5, The product we get is 120, therefore 120 Namely 5 The factorial .
Non recursive version ：

# Calculate the factorial （ Non recursive ）def recrusion(n): result = n for i in range(1, n): result *= i return resultnumber = int(input(' Please enter an integer ：'))result = recrusion(number)print("%d The factorial is ：%d" % (number, result))

The results are as follows ：

Recursive version ：

# Calculate the factorial （ recursive ）def recrusion(n): if n == 1: return 1 else: return n*recrusion(n-1)number = int(input(' Please enter an integer ：'))result = recrusion(number)print("%d The factorial is ：%d" % (number, result))

The implementation result is ：

The detailed analysis of the implementation of recursive functions is shown in the following figure ：

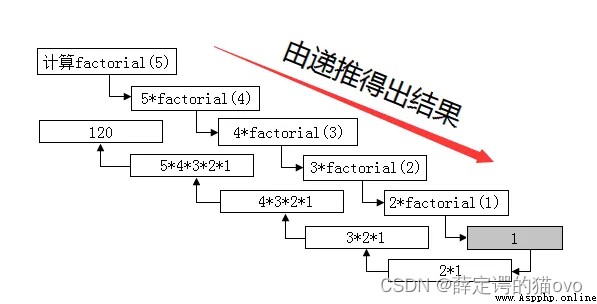
This example satisfies Two conditions of recursion ：
（1） Call the function itself
（2） Set the correct return condition

Fibonacci sequence

Another classic example of recursion —— Fibonacci sequence . The inventor of Fibonacci series , It's the Italian mathematician Leonardo · Fibonacci （Leonardo Fibonacci）. The general description is as follows ：
If there is a pair of newborn rabbits , It only takes a month for a small rabbit to grow into a big rabbit , From the third month on , The big rabbits give birth to a pair of little rabbits every month . The new rabbit will spend another month growing up , Take another month to start giving birth to rabbits … in other words , Two months after the rabbit was born , It has the ability to reproduce , After having the ability to reproduce , This pair of rabbits can give birth to a pair of little rabbits every month , If every pair of rabbits were born like this 、 mature 、 The process of procreation , And never die , What is the total number of rabbits per month ？

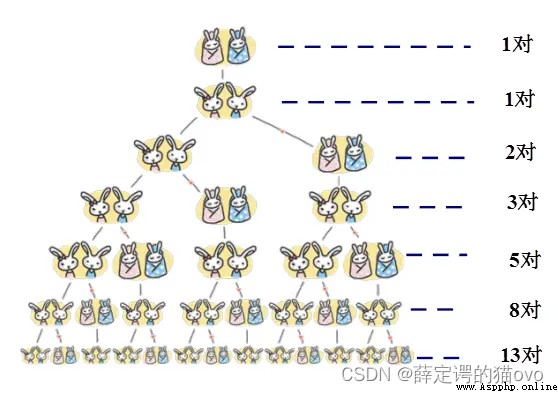
Only in the first month 1 Yes, baby rabbit .
In the second month, only 1 Yes, big rabbit .
In the third month, the big rabbit gave birth to a pair of baby rabbits , One big one small 2 To the rabbit .
In the fourth month, the big rabbit continued to give birth to a pair of baby rabbits , The little rabbit becomes the big rabbit . Two big and one small 3 To the rabbit .
….
therefore , We can get the total number of rabbits per month ：

It can be defined by mathematical functions ：

Recursive implementation ：

# Realization of Fibonacci series def fab(n): if n < 1: print(' Incorrect input ！') return -1 if n == 1 or n == 2: return 1 else: return fab(n-1) + fab(n-2)result = fab(12)if result != -1: print(" The first 12 Months in total %d To the rabbit " % result)

The implementation result is 144.
The logic of recursion is simple , however If recursion is not used properly , It's going to be inefficient . Because the implementation of recursion is that the function calls itself , Every time a function is called, you need to press the stack 、 Out of the stack 、 The operation of saving and restoring registers , So it's very time and space consuming up here .

Hanoi

French mathematician Edward · Lucas wrote an ancient Indian legend ： In the center of the world, Benares （ In northern India ） In the holy temple of , There are three jewel needles on a brass plate . When Brahman, the Hindu God, created the world , On one of the pins, from bottom to top, from big to small 64 A piece of gold , This is the so-called Hanoi tower . Day and night , There's always a monk moving these gold pieces according to the following rules ： Move only one piece at a time , No matter on which needle , Small pieces have to be on top of big ones . The monks prophesied , When all the gold pieces are moved from one needle that Brahman had put on to another , The world will be destroyed in a thunderbolt , And the vatta 、 Temples and all living beings will die together .

To solve this problem , The idea is as follows ：
（1） Before the 63 A plate from A Move to B On , Make sure the market is under the small one .
（2） Put the bottom third 64 A plate from A Move to C On .
（3） take B Upper 63 The plates move to C On .

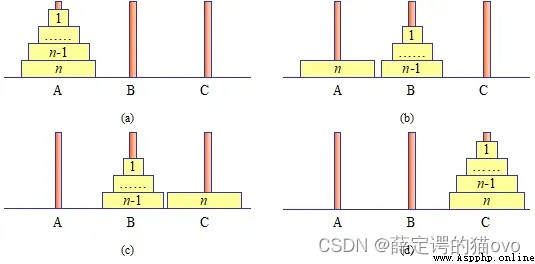
The idea of solving the problem has been improved , The key is the steps （1） And steps （3） How to execute . Because only one disc can be moved at a time , So in the process of moving , Obviously, it can only be implemented with the help of another needle . in other words , step （1） take 1~63 A plate needs help C Move to B On , step （3） take B Upper 63 With the help of A Move to C On .
therefore , Gather the new ideas into the following two questions ：
Question 1 ： take A Upper 63 With the help of C Move to B On ;
Question two ： take B Upper 63 With the help of A Move to C On .
And the corresponding The solution to question 1 and question 2 is the same as the first question just now .
Question 1 （ take A Upper 63 With the help of C Move to B On ） It can be disassembled into ：
（1） Before the 62 A plate from A Move to C On , Make sure the market is under the small market .
（2） Put the bottom third 63 The plates move to B On .
（3） take C Upper 62 The plates move to B On .
Question two （ take B Upper 63 With the help of A Move to C On ） It can be disassembled into ：
（1） Before the 62 A plate from B Move to A On , Make sure the market is under the small market .
（2） Put the bottom third 63 The plates move to C On .
（3） take A Upper 62 The plates move to C On .
therefore , This problem can be solved by recursion ：

# The hanotta problem def hanoi(n, a, b, c): # Will be the first n Layer from a With the help of b Move to c if n == 1: print(a, '-->', c) # If there is only one floor , Directly from a Move to c else: hanoi(n-1, a, c, b) # Before the n-1 A plate from a Move to b On print(a, '-->', c) # Put the bottom third 64 A plate from a Move to c On hanoi(n-1, b, a ,c) # take b Upper 63 The plates move to c On n = int(input(' Please enter the number of floors of Hanoi tower ：'))hanoi(n, 'A', 'B', 'C')

author ： Schrodinger's cat ovo

Game programming , A game development favorite ~

If the picture is not displayed for a long time , Please use Chrome Kernel browser .