樹的概念及其應用（Python）

樹的概念及其應用（Python）

• • 1. 樹
  • 2. 二叉樹
  • • 1.1 二叉樹的前序遍歷
    • 1.2 二叉樹的中序遍歷
    • 1.3 二叉樹的後序遍歷
    • 1.4 二叉樹的應用
    • • 104. 二叉樹的最大深度。
      • 543. 二叉樹的直徑。

1. 樹

樹是一種由節點（node）和邊（edges）構成層級關系的結構。

如果你了解 linux 文件結構（tree 命令），它的結構也是一棵樹。

我們快速看下樹涉及到的一些概念：

• 根節點(root): 樹的最上層的節點，任何非空的樹都有一個節點
• 路徑(path): 從起始節點到終止節點經歷過的邊
• 父親(parent)：除了根節點，每個節點的上一層邊連接的節點就是它的父親(節點)
• 孩子(children): 每個節點由邊指向的下一層節點
• 兄弟(siblings): 同一個父親並且處在同一層的節點
• 子樹(subtree): 每個節點包含它所有的後代組成的子樹
• 葉子節點(leaf node): 沒有孩子的節點成為葉子節點

2. 二叉樹

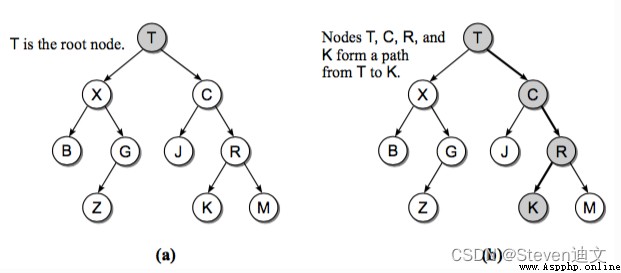
二叉樹是樹結構裡面最常用的一種樹結構，其實二叉樹就是一種簡單的樹。

二叉樹的每個節點最多包含兩個孩子。

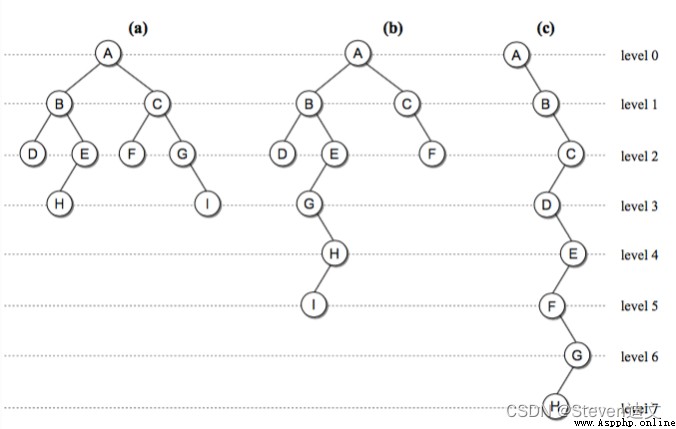
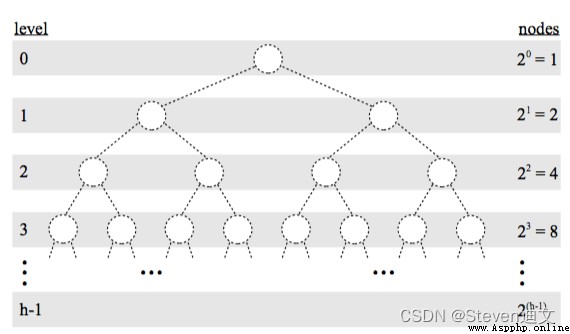
從上邊的圖來看幾個二叉樹的概念：

• 節點深度(depth): 節點對應的 level 數字。
• 樹的高度(height): 二叉樹的高度就是 level 數 + 1，因為 level 從 0開始計算的。
• 樹的寬度(width): 二叉樹的寬度指的是包含最多節點的層級的節點數。
• 樹的 size：二叉樹的節點總個數。

一棵 size 為 n 的二叉樹高度最多可以是 n，最小的高度是 ⌊lgn⌋+1，這裡 log 以 2 為底簡寫為 lgn。

1.1 二叉樹的前序遍歷

一棵二叉樹的前序遍歷結果 = 根節點 + 左子樹的前序遍歷結果 + 右子樹的前序遍歷結果。

可以理解為有序的遍歷二叉樹。

class Solution:
def preorderTraversal(self, root:TreeNode) -> List[int]:
self.res = []
self.traverse(root) #從 root 開始遍歷
return self.res # 返回的是 list
def traverse(self, root: TreeNode):
if root == None:
return
self.res.append(root.val) # 前序遍歷位置
self.traverse(root.left)
self.traverse(root.right)

1.2 二叉樹的中序遍歷

二叉樹的中序遍歷，一般在二叉搜索樹（BST）中最為常用。

你完全可以把 BST 的中序遍歷認為是遍歷有序數組。

class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
self.res = []
self.traverse(root)
return self.res
def traverse(self, root: TreeNode):
if root == None:
return
self.traverse(root.left)
self.res.append(root.val) #中序遍歷位置
self.traverse(root.right)

1.3 二叉樹的後序遍歷

後序遍歷通過遞歸的返回，返回了二叉樹子節點的信息。

class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
self.res = []
self.traverse(root)
return self.res
def traverse(self, root: TreeNode):
if root == None:
return
self.traverse(root.left)
self.traverse(root.right)
self.res.append(root.val) #後續遍歷位置

1.4 二叉樹的應用

對於二叉樹的遍歷，前序遍歷執行是自頂向下的，而後序遍歷執行是自底向上的。

以上三種遍歷過程是通過遞歸來實現的，也是 DFS 在二叉樹中的應用 。

在應用中，二叉樹的遞歸方法使用可以分兩類思路：

• 第一類是直接遍歷一遍二叉樹，對應前序遍歷。
• 第二類是分解問題，變為通過子問題求解，對應後序遍歷。

遇到問題是否可以通過遍歷一遍二叉樹得到答案**（前序遍歷）**？

如果不能的話，是否可以通過分解問題，用子問題（子樹）的答案推導出原問題的答案**（後序遍歷）**。

用幾個例子來看一下：

104. 二叉樹的最大深度。

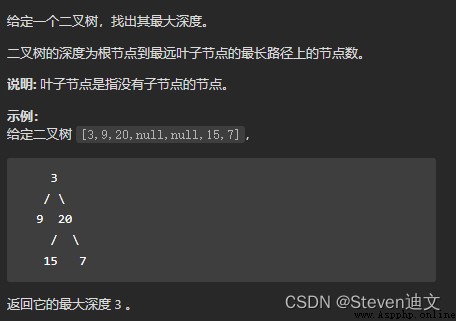
求二叉樹的最大深度，也就是求這棵樹的左右子樹深度最大的值，直接遍歷二叉樹就能解決此問題。

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
return self.traverse(root)
def traverse(self, root):
if not root:
return 0
return max(self.traverse(root.left), self.traverse(root.right)) + 1 # 遞歸，左右子樹的最大深度
# 加 1 是加上根節點的深度。

543. 二叉樹的直徑。

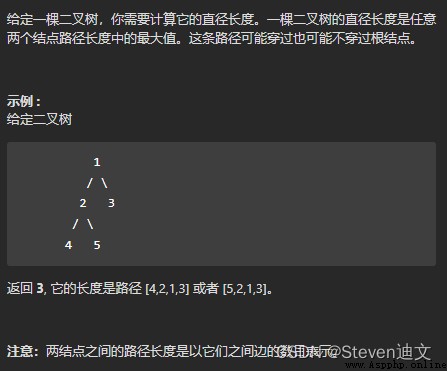
根據題目，直徑可以理解為任意節點的左右子樹的最大深度之和。

那麼直接的想法是對每個節點計算左右子樹的最大高度，得出每個節點的直徑，從而得出最大的那個直徑。

解決這題的關鍵在於，每一條二叉樹的直徑長度，就是一個節點的左右子樹的最大深度之和。

這就是把原問題分解為子問題的方法。

class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
self.max = 0
self.traverse(root)
return self.max
def traverse(self, root):
if not root:
return 0
l = self.traverse(root.left) #求該節點左子樹的深度
r = self.traverse(root.right)#求該節點右子樹的深度
self.max = max(self.max, l+r) # 後續遍歷更新最大的直徑
return max(l,r) + 1 #這也是後序遍歷的位置。
# 由於利用後序遍歷從低向上計算子問題，其含義是返回當前節點（子節點）中左右子樹深度最大的那一個，用於後續計算最大路徑。