A tree is a (node) He Bian (edges) A structure that forms a hierarchical relationship .
If you know linux File structure (tree command ), Its structure is also a tree .
Let's take a quick look at some of the concepts involved in the tree :
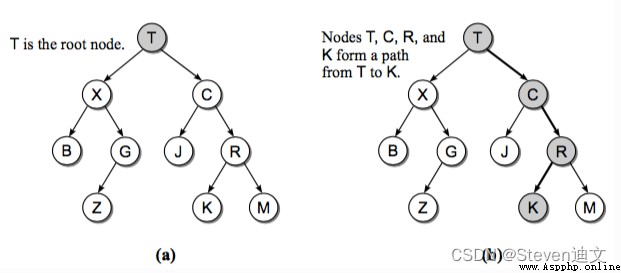
Binary tree is the most commonly used tree structure , In fact, a binary tree is a simple tree .
Each node of the binary tree contains at most two children .
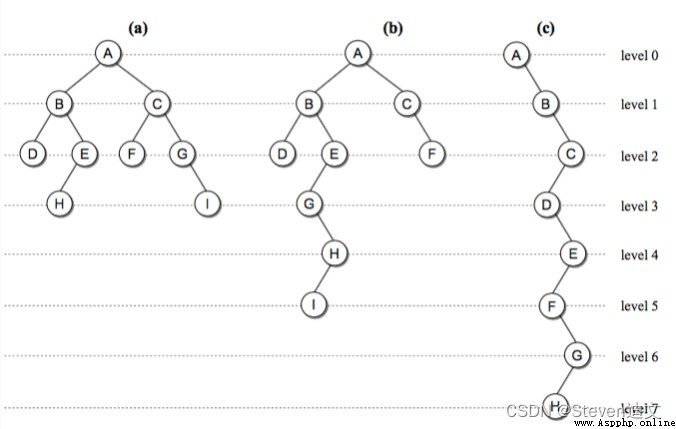
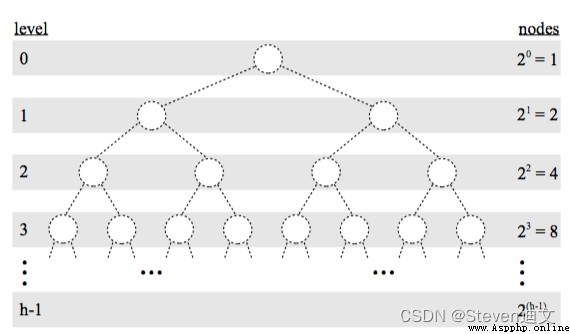
From the figure above, we can see some concepts of binary tree :
A tree size by n The maximum height of a binary tree can be n, The minimum height is ⌊lgn⌋+1, here log With 2 At the bottom, it's abbreviated as lgn.
The preorder traversal result of a binary tree = The root node + The result of preorder traversal of left subtree + The result of preorder traversal of the right subtree .
It can be understood as an orderly traversal of a binary tree .
class Solution:
def preorderTraversal(self, root:TreeNode) -> List[int]:
self.res = []
self.traverse(root) # from root To traverse the
return self.res # The return is list
def traverse(self, root: TreeNode):
if root == None:
return
self.res.append(root.val) # Preorder traversal position
self.traverse(root.left)
self.traverse(root.right)
Middle order traversal of binary trees , Usually in binary search tree (BST) Most commonly used in .
You can do that BST The middle order traversal of is considered to be traversing an ordered array .
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
self.res = []
self.traverse(root)
return self.res
def traverse(self, root: TreeNode):
if root == None:
return
self.traverse(root.left)
self.res.append(root.val) # Middle order traversal position
self.traverse(root.right)
Postorder traversal returns through recursion , Returns the information of the child nodes of the binary tree .
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
self.res = []
self.traverse(root)
return self.res
def traverse(self, root: TreeNode):
if root == None:
return
self.traverse(root.left)
self.traverse(root.right)
self.res.append(root.val) # Subsequent traversal position
For the traversal of binary tree , The preorder traversal is performed from top to bottom , The execution of post order traversal is bottom-up .
The above three traversal processes are realized by recursion , It's also DFS Application in binary tree .
In the application , The recursive method of binary tree can be divided into two categories :
If you encounter a problem, can you get the answer by traversing the binary tree **( The former sequence traversal )**?
If not , Is it possible to decompose the problem , Use subproblem ( subtree ) The answer to the original question **( After the sequence traversal )**.
Take a few examples :
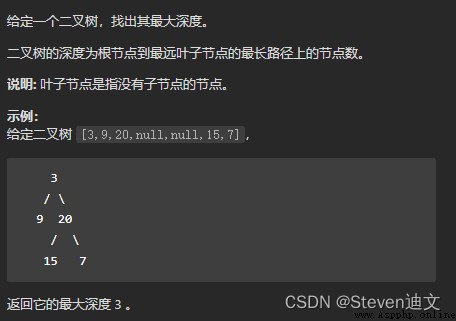
Find the maximum depth of a binary tree , That is to find the maximum depth of the left and right subtrees of the tree , Directly traversing the binary tree can solve this problem .
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
return self.traverse(root)
def traverse(self, root):
if not root:
return 0
return max(self.traverse(root.left), self.traverse(root.right)) + 1 # recursive , The maximum depth of the left and right subtrees
# Add 1 Is the depth of the root node .
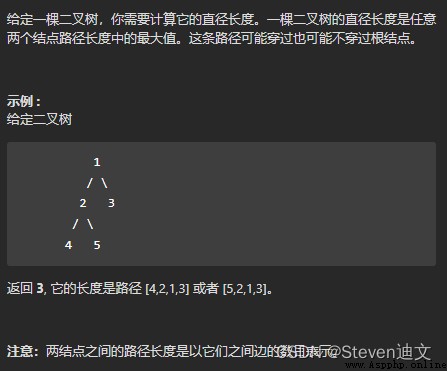
According to the title , The diameter can be understood as the sum of the maximum depths of the left and right subtrees of any node .
The direct idea is to calculate the maximum height of the left and right subtrees for each node , Get the diameter of each node , To get the largest diameter .
The key to solving this problem is , The diameter and length of each binary tree , Is the sum of the maximum depths of the left and right subtrees of a node .
This is the way to decompose the original problem into subproblems .
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
self.max = 0
self.traverse(root)
return self.max
def traverse(self, root):
if not root:
return 0
l = self.traverse(root.left) # Find the depth of the left subtree of the node
r = self.traverse(root.right)# Find the depth of the right subtree of the node
self.max = max(self.max, l+r) # Subsequent iterations update the maximum diameter
return max(l,r) + 1 # This is also the location of the postorder traversal .
# Since the subproblem is calculated from low to high by using post order traversal , It means to return the current node ( Child node ) The one with the largest depth of the left and right subtrees , Used for subsequent calculation of maximum path .