python與分形0020 - Stack of Hexagons

分形介紹

分形是一個悖論。

它驚人的簡單，卻又無限的復雜。

它很新，卻又比塵埃更古老。

分形是什麼？它們是從哪裡來的？我們為什麼要在乎？

20世紀非傳統的數學家Benoit Mandelbrot在1975年從拉丁詞fractus(意思是不規則的或破碎的)創造了分形這個詞。

我們周圍到處都可以看到分形的影子。

從最基本的角度看，分形是重復模式或公式的視覺表達，開始時很簡單，然後逐漸變得更復雜。

在數學中，分形是歐氏空間的子集，其分形維數嚴格超過其拓撲維數。

分形在不同的尺度上表現相同，如Mandelbrot集合的連續放大。

分形通常在越來越小的尺度上表現出類似的模式，這種特性稱為自相似性，也稱為擴展對稱或展開對稱。

如果這種復制在每個尺度上都完全相同，就像在門格爾海綿中一樣，那麼它就被稱為仿射自相似。

分形幾何屬於度量理論的數學分支。

分形結果

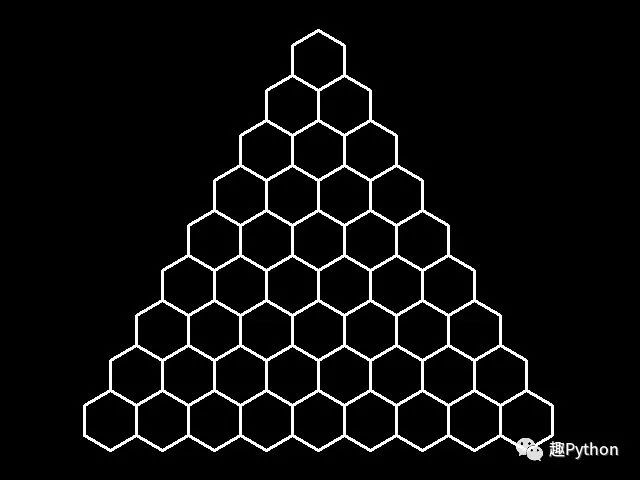
原理參考上一篇：python與分形0019 - 【教程】Stack of Circles 原創

分形源碼

# coding: utf-8
import turtle
import math
import time
window = turtle.Screen()
window.screensize()
window.setup(width=1.0, height=1.0, startx=None, starty=None)
turtle.speed(5)
turtle.hideturtle()
#turtle.tracer(0)
turtle.bgcolor('black')
turtle.color('white')
turtle.pensize(3)
def draw_vertical_hexagon(start_pos, length):
    turtle.penup()
    turtle.goto(start_pos)
    turtle.seth(90)
    turtle.pendown()
    for i in range(6):
        turtle.fd(length)
        turtle.right(60)
def stack_hexagons(x0, y0, r, stacks):
    draw_vertical_hexagon((x0,y0), r)
    if stacks > 1:
        for s in range(1, stacks):
            x0 -= 0.5*math.sqrt(3)*r
            y0 -= 1.5*r
            for _ in range(s+1):
                draw_vertical_hexagon((x0+_*math.sqrt(3)*r,y0), r)
                turtle.update()
#time.sleep(5)
r = 30
x0 = 0
y0 = 300
stack_hexagons(x0, y0, r, 9)

分形視頻