Fractal is a paradox .
It's surprisingly simple , But infinite complexity .
It's new , But older than dust .
What is fractal ? Where did they come from ? Why should we care about ?
20 An unconventional mathematician of the th century Benoit Mandelbrot stay 1975 From Latin words fractus( It means irregular or broken ) Created the word fractal .
We can see the shadow of fractal everywhere .
From the most basic point of view , Fractal is the visual expression of repeated patterns or formulas , It was simple at first , Then it gradually becomes more complex .
In mathematics , Fractal is a subset of Euclidean space , Its fractal dimension strictly exceeds its topological dimension .
Fractal is the same on different scales , Such as Mandelbrot Continuous amplification of sets .
Fractal usually shows similar patterns on smaller and smaller scales , This property is called self similarity , Also called extended symmetry or expanded symmetry .
If this replication is identical on every scale , Just like in Menger sponge , Then it is called affine self similarity .
Fractal geometry belongs to the mathematical branch of measurement theory .
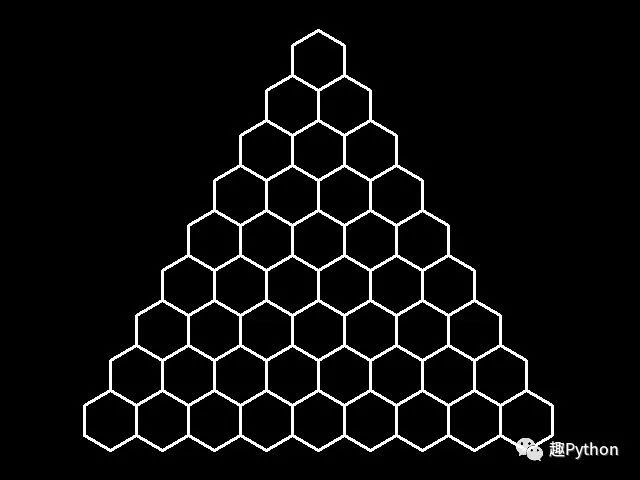
Refer to the previous article for the principle :python And fractal 0019 - 【 course 】Stack of Circles original
# coding: utf-8
import turtle
import math
import time
window = turtle.Screen()
window.screensize()
window.setup(width=1.0, height=1.0, startx=None, starty=None)
turtle.speed(5)
turtle.hideturtle()
#turtle.tracer(0)
turtle.bgcolor('black')
turtle.color('white')
turtle.pensize(3)
def draw_vertical_hexagon(start_pos, length):
turtle.penup()
turtle.goto(start_pos)
turtle.seth(90)
turtle.pendown()
for i in range(6):
turtle.fd(length)
turtle.right(60)
def stack_hexagons(x0, y0, r, stacks):
draw_vertical_hexagon((x0,y0), r)
if stacks > 1:
for s in range(1, stacks):
x0 -= 0.5*math.sqrt(3)*r
y0 -= 1.5*r
for _ in range(s+1):
draw_vertical_hexagon((x0+_*math.sqrt(3)*r,y0), r)
turtle.update()
#time.sleep(5)
r = 30
x0 = 0
y0 = 300
stack_hexagons(x0, y0, r, 9)

