2022.2.10 to update ,Python There are ready-made packages that can directly call .
geographiclib library 
https://pypi.org/project/geographiclib/ See the blog for instructions ：
python Calculate the distance and azimuth of two points on the earth （bearing） My bag geographiclib_ Ziyi's blog -CSDN Blog _geodesic python Calculate the distance and azimuth of two points on the map through longitude and latitude , The result of Baidu is the function formula written by many individuals , however python So many bags , There can be no such calculation , Self built functions are certainly not as good as public packages , Later, I found one https://stackoverflow.com/questions/17624310/geopy-calculating-gps-heading-bearing Use the geographiclib package...
https://blog.csdn.net/qq_27361945/article/details/79552213
It's just two simple steps , You can get the distance and azimuth of the two longitude and latitude points . There is no need to bother with the solid geometry .
Open... With administrator cmd window , Enter the following command ：
pip install geographiclib# -*- coding:utf-8 -*-
# python3 Code
from geographiclib.geodesic import Geodesic
# Note that the order of the parameters is a bit strange , Namely spot 1 latitude , spot 1 longitude , spot 2 latitude , spot 2 longitude
# North latitude and east longitude are positive numbers , The south latitude and west longitude are negative
geodict = Geodesic.WGS84.Inverse(-41.32, 174.81, 40.96, -5.50)
# distance float Format
distance = geodict['s12']
# spot 1 Reference azimuth
# Azimuth is from the north line of a point , Horizontal angle between clockwise direction and target direction line
az = geodict['azi1']
# The actual measurement is accurate In this part, I refer to the following ： Calculate the distance between the two places according to longitude and latitude _weixin_34218890 The blog of -CSDN Blog Recent work needs , We searched the Internet for a method to calculate the distance between the two places according to longitude and latitude , Discovery is either geometric , drawing 、 Make a bunch of auxiliary lines , Then prove the reasoning , Or you can set up a formula without saying a word . This article introduces an easy to understand way to find this distance .0b00 The earth is an irregular ellipsoid 、 For the sake of simplicity, we calculate it as a sphere . The shortest distance between two places on a sphere is the length of the inferior arc of the great circle passing through two points . Ideas as follows : Arc length ← String length ( Two point distance )...https://blog.csdn.net/weixin_34218890/article/details/88740639
The explanation of the principle in the original text is very clear , The method used in this article is ： Convert the longitude and latitude points into three-dimensional rectangular coordinate system points , Then calculate the distance according to the solid geometry knowledge . The method is simple and clear , Suitable for low precision 、 A short distance scene .
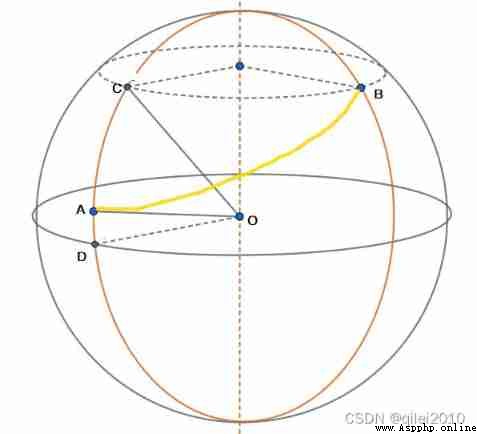
The earth is an irregular ellipsoid 、 For the sake of simplicity, we calculate it as a sphere .
The shortest distance between two places on a sphere is the length of the inferior arc of the great circle passing through two points .（ Inferior arc , The shorter arc ）
Ideas as follows :
Arc length ← String length ( Two point distance ) ← Two point coordinates ( Rectangular coordinates ) ← Longitude and latitude Solid geometry knowledge is required ：
set up
be A The three-dimensional coordinates of can be expressed as :
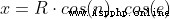
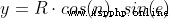
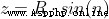
This is too simple , skip
This can draw a picture , Help you understand ：
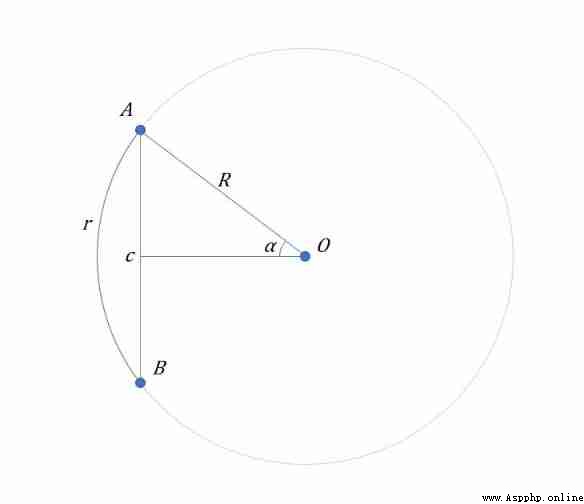
Now the chord length is known c , radius R , Required arc r The length of
It's very simple , Just find out ∠a （ Horn alpha ） Size ：
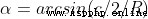
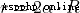
# -*- coding:utf-8 -*-
# python3
import math
def getDistance(e1,n1,e2,n2):
'''
Get the distance between two longitudes and latitudes
:param e1: spot 1 East longitude of , Company : angle , If it is the Western longitude, it is negative
:param n1: spot 1 North latitude of , Company : angle , If it is south latitude, it is negative
:param e2:
:param n2:
:return: The distance between two longitudes and latitudes , Unit kilometer
'''
R = 6378.137 # Earth radius , Unit kilometer
# Convert longitude and latitude degrees to radians
def getPoint(e,n):
e *= math.pi / 180.0
n *= math.pi / 180.0
# here R* Be removed , It is equivalent to first finding the distance between two points on the unit circle , Finally, I will enlarge the distance R times
return (math.cos(n)*math.cos(e), math.cos(n)*math.sin(e), math.sin(n))
# Calculate the bevel length of 3D space
def myHypot(a,b,c):
return math.sqrt(a**2+b**2+c**2)
a = getPoint(e1,n1)
b = getPoint(e2,n2)
c = myHypot(a[0] - b[0], a[1] - b[1], a[2] - b[2])
r = math.asin(c/2)*2*R
return r
d = getDistance(114.123456,30.123456,114.124567,30.123457)
print(d*1000)
There are many ways to calculate the relative angle of two longitude and latitude points , Detailed reference materials 1. Here we will only talk about the principle of one of the simplest methods , Because this article only lists the formula , The principle of the formula is not explained , I would like to add here .
Scope of application ： The longitude difference and latitude difference are converted into the ground distance, and then the plane geometry knowledge is used to solve , So it can only be used for short distance calculation , Mid latitude recommendations 40km following . Because the calculation is simpler , So it has relative advantages .
It is known that ：Aj,Aw,Bj,Bw
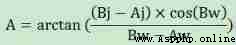
When
B The point is in the first quadrant and Y Shaft positive half shaft ,Bearing=A;
B In the second quadrant ,Bearing=360+A;
B In the third and fourth quadrants and Y Axis negative half axis ,Bearing=180+A.
For some systems , Then set it separately B be located X The value on the positive and negative half axes is OK , Some systems can return arctan（X/0）=90.
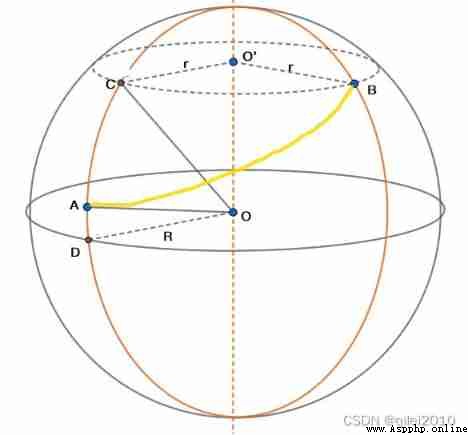
mathematical description ：
Already started A Point latitude and longitude （Aj,Aw）, End B Point latitude and longitude （Bj,Bw）, The radius of the earth is R, seek horn CAB, That is to say spot B Relative point A The azimuth of . among , Azimuth is from the north line of a point , Horizontal angle between clockwise direction and target direction line .
Problem solving ：
When A spot B When the points are close to each other , Simply think ABC It's a flat triangle .∠CAB Shorthand for ∠A, Arc BC Length simple writing BC, Arc AC The length is abbreviated as AC, Then there are ：
tan∠A = BC / AC
be
∠A = arctan (BC / AC)Then the problem becomes , How to find BC and AC.
1) seek AC
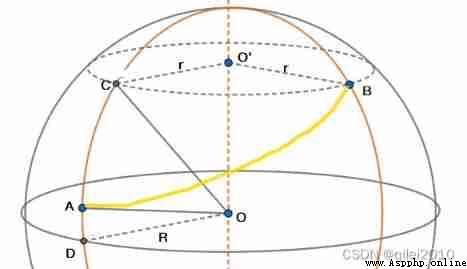
This is simpler ,C Point and end B The point is at the same latitude , therefore ∠COD Namely End B The latitude value of the point （ The definition of latitude ）,∠AOD It's the starting point A Latitude value of . namely
∠COD = Bw
∠AOD = Aw
∠COA = Bw - Aw
AC = R * ( ∠COA * π / 180 )
AC = R * ( (Bw - Aw) * π / 180 )among ,∠COA * π / 180 It's to make ∠COA The angle value of is converted to radian value .
2) seek BC
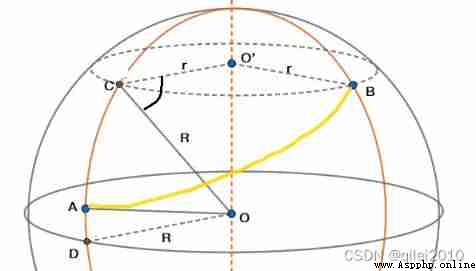
stay CO'B The latitude circle is the middle of the small circle ,BC Arc length = Small circle radius r × horn CO'B radian , So the key is to find the radius of the small circle r.
According to geometric knowledge , Yes
r = R * cos∠O'CO
Because of ∠O'CO = ∠COD, among ∠COD Namely B spot C Latitude of point
therefore r = R * cos∠COD = R * cos Bwand ∠CO'B namely AB The difference between the longitude of two points ：
∠CO'B = Bj-Ajtherefore , You can get
BC = r * horn CO'B radian
BC = r * (Bj-Aj）*π/180
BC = R * cosBw * (Bj-Aj）*π/180 3) Seeking angle A
BC
BC = R * cosBw * (Bj-Aj）*π/180
AC = R * ( (Bw - Aw) * π / 180 )
AC And BC There's... In it R, They are divided by each other R
BC / AC = (Bj-Aj)cosBw / Bw-Aw
∠A = arctan (BC / AC)
∠A = arctan( (Bj-Aj)cosBw / Bw-Aw )therefore , Get the formula in the picture .
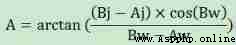
A very comprehensive and detailed article ：
[ Reprint ] Calculate the azimuth and distance according to the longitude and latitude of two points , etc. _ The rabbits blossomed _ Sina blog [ Reprint ] Calculate the azimuth and distance according to the longitude and latitude of two points , etc. _ The rabbits blossomed _ Sina blog , The rabbits blossomed ,http://blog.sina.com.cn/s/blog_5e7960620101vi0d.html
