資料轉自(GitHub地址):https://github.com/wesm/pydata-book 有需要的朋友可以自行去github下載
本章包括了一些雜亂的章節,不需要仔細研究。
NumPy的ndarray提供了一種將同質數據塊(可以是連續或跨越)解釋為多維數組對象的方式。正如你之前所看到的那樣,數據類型(dtype)決定了數據的解釋方式,比如浮點數、整數、布爾值等。
ndarray如此強大的部分原因是所有數組對象都是數據塊的一個跨度視圖(strided view)。你可能想知道數組視圖arr[::2,::-1]不復制任何數據的原因是什麼。簡單地說,ndarray不只是一塊內存和一個dtype,它還有跨度信息,這使得數組能以各種步幅(step size)在內存中移動。更准確地講,ndarray內部由以下內容組成:
圖A-1簡單地說明了ndarray的內部結構。
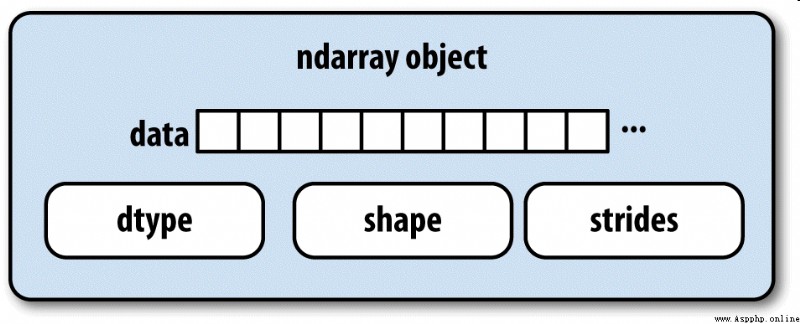
例如,一個10×5的數組,其形狀為(10,5):
In [10]: np.ones((10, 5)).shape
Out[10]: (10, 5)
一個典型的(C順序,稍後將詳細講解)3×4×5的float64(8個字節)數組,其跨度為(160,40,8) —— 知道跨度是非常有用的,通常,跨度在一個軸上越大,沿這個軸進行計算的開銷就越大:
In [11]: np.ones((3, 4, 5), dtype=np.float64).strides
Out[11]: (160, 40, 8)
雖然NumPy用戶很少會對數組的跨度信息感興趣,但它們卻是構建非復制式數組視圖的重要因素。跨度甚至可以是負數,這樣會使數組在內存中後向移動,比如在切片obj[::-1]或obj[:,::-1]中就是這樣的。
你可能偶爾需要檢查數組中所包含的是否是整數、浮點數、字符串或Python對象。因為浮點數的種類很多(從float16到float128),判斷dtype是否屬於某個大類的工作非常繁瑣。幸運的是,dtype都有一個超類(比如np.integer和np.floating),它們可以跟np.issubdtype函數結合使用:
In [12]: ints = np.ones(10, dtype=np.uint16)
In [13]: floats = np.ones(10, dtype=np.float32)
In [14]: np.issubdtype(ints.dtype, np.integer)
Out[14]: True
In [15]: np.issubdtype(floats.dtype, np.floating)
Out[15]: True
調用dtype的mro方法即可查看其所有的父類:
In [16]: np.float64.mro()
Out[16]:
[numpy.float64,
numpy.floating,
numpy.inexact,
numpy.number,
numpy.generic,
float,
object]
然後得到:
In [17]: np.issubdtype(ints.dtype, np.number)
Out[17]: True
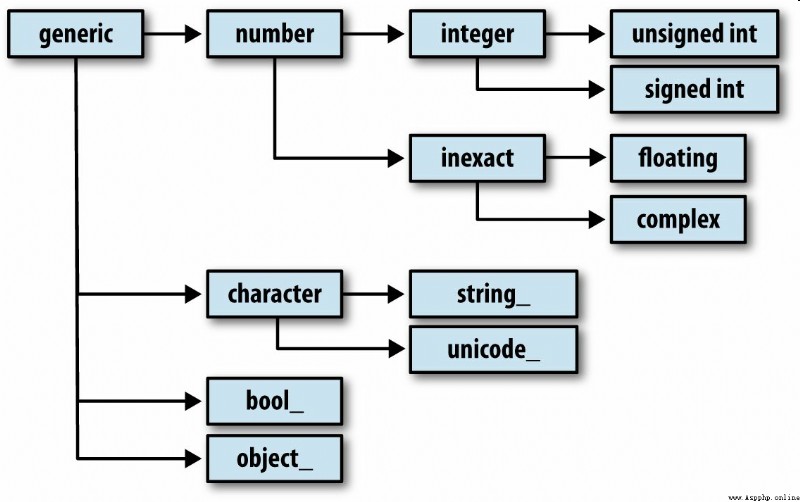
大部分NumPy用戶完全不需要了解這些知識,但是這些知識偶爾還是能派上用場的。圖A-2說明了dtype體系以及父子類關系。
除花式索引、切片、布爾條件取子集等操作之外,數組的操作方式還有很多。雖然pandas中的高級函數可以處理數據分析工作中的許多重型任務,但有時你還是需要編寫一些在現有庫中找不到的數據算法。
多數情況下,你可以無需復制任何數據,就將數組從一個形狀轉換為另一個形狀。只需向數組的實例方法reshape傳入一個表示新形狀的元組即可實現該目的。例如,假設有一個一維數組,我們希望將其重新排列為一個矩陣(結果見圖A-3):
In [18]: arr = np.arange(8)
In [19]: arr
Out[19]: array([0, 1, 2, 3, 4, 5, 6, 7])
In [20]: arr.reshape((4, 2))
Out[20]:
array([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
多維數組也能被重塑:
In [21]: arr.reshape((4, 2)).reshape((2, 4))
Out[21]:
array([[0, 1, 2, 3],
[4, 5, 6, 7]])
作為參數的形狀的其中一維可以是-1,它表示該維度的大小由數據本身推斷而來:
In [22]: arr = np.arange(15)
In [23]: arr.reshape((5, -1))
Out[23]:
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14]])
與reshape將一維數組轉換為多維數組的運算過程相反的運算通常稱為扁平化(flattening)或散開(raveling):
In [27]: arr = np.arange(15).reshape((5, 3))
In [28]: arr
Out[28]:
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14]])
In [29]: arr.ravel()
Out[29]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])
如果結果中的值與原始數組相同,ravel不會產生源數據的副本。flatten方法的行為類似於ravel,只不過它總是返回數據的副本:
In [30]: arr.flatten()
Out[30]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])
數組可以被重塑或散開為別的順序。這對NumPy新手來說是一個比較微妙的問題,所以在下一小節中我們將專門講解這個問題。
NumPy允許你更為靈活地控制數據在內存中的布局。默認情況下,NumPy數組是按行優先順序創建的。在空間方面,這就意味著,對於一個二維數組,每行中的數據項是被存放在相鄰內存位置上的。另一種順序是列優先順序,它意味著每列中的數據項是被存放在相鄰內存位置上的。
由於一些歷史原因,行和列優先順序又分別稱為C和Fortran順序。在FORTRAN 77中,矩陣全都是列優先的。
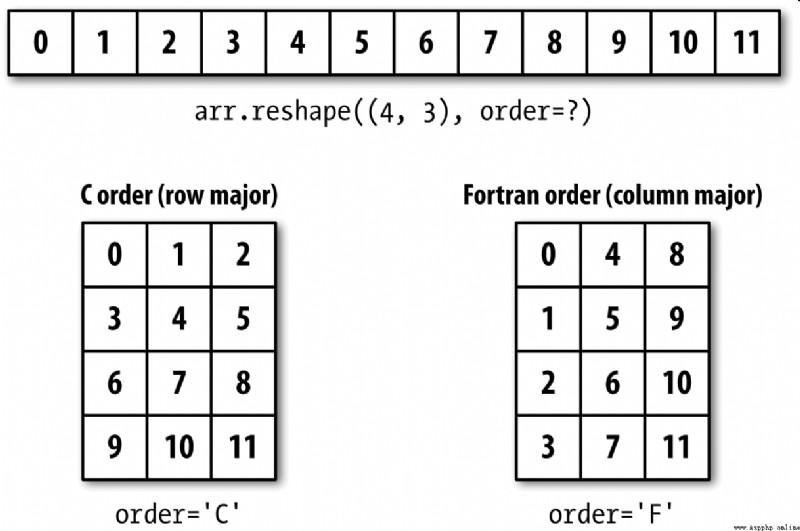
像reshape和reval這樣的函數,都可以接受一個表示數組數據存放順序的order參數。一般可以是’C’或’F’(還有’A’和’K’等不常用的選項,具體請參考NumPy的文檔)。圖A-3對此進行了說明:
In [31]: arr = np.arange(12).reshape((3, 4))
In [32]: arr
Out[32]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
In [33]: arr.ravel()
Out[33]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
In [34]: arr.ravel('F')
Out[34]: array([ 0, 4, 8, 1, 5, 9, 2, 6, 10, 3, 7, 11])

二維或更高維數組的重塑過程比較令人費解(見圖A-3)。C和Fortran順序的關鍵區別就是維度的行進順序:
numpy.concatenate可以按指定軸將一個由數組組成的序列(如元組、列表等)連接到一起:
In [35]: arr1 = np.array([[1, 2, 3], [4, 5, 6]])
In [36]: arr2 = np.array([[7, 8, 9], [10, 11, 12]])
In [37]: np.concatenate([arr1, arr2], axis=0)
Out[37]:
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
In [38]: np.concatenate([arr1, arr2], axis=1)
Out[38]:
array([[ 1, 2, 3, 7, 8, 9],
[ 4, 5, 6, 10, 11, 12]])
對於常見的連接操作,NumPy提供了一些比較方便的方法(如vstack和hstack)。因此,上面的運算還可以表達為:
In [39]: np.vstack((arr1, arr2))
Out[39]:
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
In [40]: np.hstack((arr1, arr2))
Out[40]:
array([[ 1, 2, 3, 7, 8, 9],
[ 4, 5, 6, 10, 11, 12]])
與此相反,split用於將一個數組沿指定軸拆分為多個數組:
In [41]: arr = np.random.randn(5, 2)
In [42]: arr
Out[42]:
array([[-0.2047, 0.4789],
[-0.5194, -0.5557],
[ 1.9658, 1.3934],
[ 0.0929, 0.2817],
[ 0.769 , 1.2464]])
In [43]: first, second, third = np.split(arr, [1, 3])
In [44]: first
Out[44]: array([[-0.2047, 0.4789]])
In [45]: second
Out[45]:
array([[-0.5194, -0.5557],
[ 1.9658, 1.3934]])
In [46]: third
Out[46]:
array([[ 0.0929, 0.2817],
[ 0.769 , 1.2464]])
傳入到np.split的值[1,3]指示在哪個索引處分割數組。
表A-1中列出了所有關於數組連接和拆分的函數,其中有些是專門為了方便常見的連接運算而提供的。
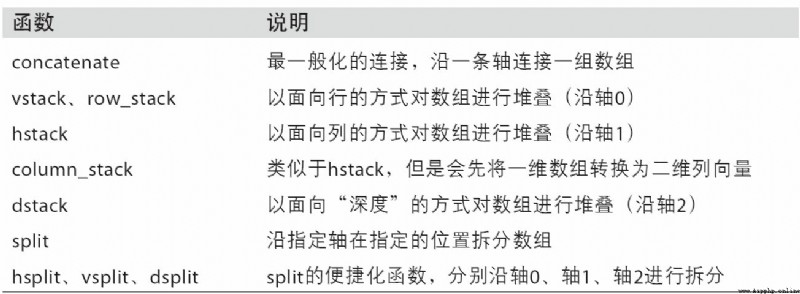
NumPy命名空間中有兩個特殊的對象——r_和c_,它們可以使數組的堆疊操作更為簡潔:
In [47]: arr = np.arange(6)
In [48]: arr1 = arr.reshape((3, 2))
In [49]: arr2 = np.random.randn(3, 2)
In [50]: np.r_[arr1, arr2]
Out[50]:
array([[ 0. , 1. ],
[ 2. , 3. ],
[ 4. , 5. ],
[ 1.0072, -1.2962],
[ 0.275 , 0.2289],
[ 1.3529, 0.8864]])
In [51]: np.c_[np.r_[arr1, arr2], arr]
Out[51]:
array([[ 0. , 1. , 0. ],
[ 2. , 3. , 1. ],
[ 4. , 5. , 2. ],
[ 1.0072, -1.2962, 3. ],
[ 0.275 , 0.2289, 4. ],
[ 1.3529, 0.8864, 5. ]])
它還可以將切片轉換成數組:
In [52]: np.c_[1:6, -10:-5]
Out[52]:
array([[ 1, -10],
[ 2, -9],
[ 3, -8],
[ 4, -7],
[ 5, -6]])
r_和c_的具體功能請參考其文檔。
對數組進行重復以產生更大數組的工具主要是repeat和tile這兩個函數。repeat會將數組中的各個元素重復一定次數,從而產生一個更大的數組:
In [53]: arr = np.arange(3)
In [54]: arr
Out[54]: array([0, 1, 2])
In [55]: arr.repeat(3)
Out[55]: array([0, 0, 0, 1, 1, 1, 2, 2, 2])
筆記:跟其他流行的數組編程語言(如MATLAB)不同,NumPy中很少需要對數組進行重復(replicate)。這主要是因為廣播(broadcasting,我們將在下一節中講解該技術)能更好地滿足該需求。
默認情況下,如果傳入的是一個整數,則各元素就都會重復那麼多次。如果傳入的是一組整數,則各元素就可以重復不同的次數:
In [56]: arr.repeat([2, 3, 4])
Out[56]: array([0, 0, 1, 1, 1, 2, 2, 2, 2])
對於多維數組,還可以讓它們的元素沿指定軸重復:
In [57]: arr = np.random.randn(2, 2)
In [58]: arr
Out[58]:
array([[-2.0016, -0.3718],
[ 1.669 , -0.4386]])
In [59]: arr.repeat(2, axis=0)
Out[59]:
array([[-2.0016, -0.3718],
[-2.0016, -0.3718],
[ 1.669 , -0.4386],
[ 1.669 , -0.4386]])
注意,如果沒有設置軸向,則數組會被扁平化,這可能不會是你想要的結果。同樣,在對多維進行重復時,也可以傳入一組整數,這樣就會使各切片重復不同的次數:
In [60]: arr.repeat([2, 3], axis=0)
Out[60]:
array([[-2.0016, -0.3718],
[-2.0016, -0.3718],
[ 1.669 , -0.4386],
[ 1.669 , -0.4386],
[ 1.669 , -0.4386]])
In [61]: arr.repeat([2, 3], axis=1)
Out[61]:
array([[-2.0016, -2.0016, -0.3718, -0.3718, -0.3718],
[ 1.669 , 1.669 , -0.4386, -0.4386, -0.4386]])
tile的功能是沿指定軸向堆疊數組的副本。你可以形象地將其想象成“鋪瓷磚”:
In [62]: arr
Out[62]:
array([[-2.0016, -0.3718],
[ 1.669 , -0.4386]])
In [63]: np.tile(arr, 2)
Out[63]:
array([[-2.0016, -0.3718, -2.0016, -0.3718],
[ 1.669 , -0.4386, 1.669 , -0.4386]])
第二個參數是瓷磚的數量。對於標量,瓷磚是水平鋪設的,而不是垂直鋪設。它可以是一個表示“鋪設”布局的元組:
In [64]: arr
Out[64]:
array([[-2.0016, -0.3718],
[ 1.669 , -0.4386]])
In [65]: np.tile(arr, (2, 1))
Out[65]:
array([[-2.0016, -0.3718],
[ 1.669 , -0.4386],
[-2.0016, -0.3718],
[ 1.669 , -0.4386]])
In [66]: np.tile(arr, (3, 2))
Out[66]:
array([[-2.0016, -0.3718, -2.0016, -0.3718],
[ 1.669 , -0.4386, 1.669 , -0.4386],
[-2.0016, -0.3718, -2.0016, -0.3718],
[ 1.669 , -0.4386, 1.669 , -0.4386],
[-2.0016, -0.3718, -2.0016, -0.3718],
[ 1.669 , -0.4386, 1.669 , -0.4386]])
在第4章中我們講過,獲取和設置數組子集的一個辦法是通過整數數組使用花式索引:
In [67]: arr = np.arange(10) * 100
In [68]: inds = [7, 1, 2, 6]
In [69]: arr[inds]
Out[69]: array([700, 100, 200, 600])
ndarray還有其它方法用於獲取單個軸向上的選區:
In [70]: arr.take(inds)
Out[70]: array([700, 100, 200, 600])
In [71]: arr.put(inds, 42)
In [72]: arr
Out[72]: array([ 0, 42, 42, 300, 400, 500, 42, 42,800, 900])
In [73]: arr.put(inds, [40, 41, 42, 43])
In [74]: arr
Out[74]: array([ 0, 41, 42, 300, 400, 500, 43, 40, 800, 900])
要在其它軸上使用take,只需傳入axis關鍵字即可:
In [75]: inds = [2, 0, 2, 1]
In [76]: arr = np.random.randn(2, 4)
In [77]: arr
Out[77]:
array([[-0.5397, 0.477 , 3.2489, -1.0212],
[-0.5771, 0.1241, 0.3026, 0.5238]])
In [78]: arr.take(inds, axis=1)
Out[78]:
array([[ 3.2489, -0.5397, 3.2489, 0.477 ],
[ 0.3026, -0.5771, 0.3026, 0.1241]])
put不接受axis參數,它只會在數組的扁平化版本(一維,C順序)上進行索引。因此,在需要用其他軸向的索引設置元素時,最好還是使用花式索引。
廣播(broadcasting)指的是不同形狀的數組之間的算術運算的執行方式。它是一種非常強大的功能,但也容易令人誤解,即使是經驗豐富的老手也是如此。將標量值跟數組合並時就會發生最簡單的廣播:
In [79]: arr = np.arange(5)
In [80]: arr
Out[80]: array([0, 1, 2, 3, 4])
In [81]: arr * 4
Out[81]: array([ 0, 4, 8, 12, 16])
這裡我們說:在這個乘法運算中,標量值4被廣播到了其他所有的元素上。
看一個例子,我們可以通過減去列平均值的方式對數組的每一列進行距平化處理。這個問題解決起來非常簡單:
In [82]: arr = np.random.randn(4, 3)
In [83]: arr.mean(0)
Out[83]: array([-0.3928, -0.3824, -0.8768])
In [84]: demeaned = arr - arr.mean(0)
In [85]: demeaned
Out[85]:
array([[ 0.3937, 1.7263, 0.1633],
[-0.4384, -1.9878, -0.9839],
[-0.468 , 0.9426, -0.3891],
[ 0.5126, -0.6811, 1.2097]])
In [86]: demeaned.mean(0)
Out[86]: array([-0., 0., -0.])
圖A-4形象地展示了該過程。用廣播的方式對行進行距平化處理會稍微麻煩一些。幸運的是,只要遵循一定的規則,低維度的值是可以被廣播到數組的任意維度的(比如對二維數組各列減去行平均值)。
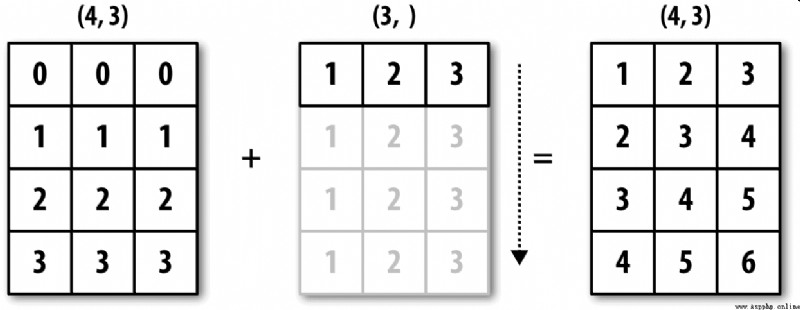
於是就得到了:

雖然我是一名經驗豐富的NumPy老手,但經常還是得停下來畫張圖並想想廣播的原則。再來看一下最後那個例子,假設你希望對各行減去那個平均值。由於arr.mean(0)的長度為3,所以它可以在0軸向上進行廣播:因為arr的後緣維度是3,所以它們是兼容的。根據該原則,要在1軸向上做減法(即各行減去行平均值),較小的那個數組的形狀必須是(4,1):
In [87]: arr
Out[87]:
array([[ 0.0009, 1.3438, -0.7135],
[-0.8312, -2.3702, -1.8608],
[-0.8608, 0.5601, -1.2659],
[ 0.1198, -1.0635, 0.3329]])
In [88]: row_means = arr.mean(1)
In [89]: row_means.shape
Out[89]: (4,)
In [90]: row_means.reshape((4, 1))
Out[90]:
array([[ 0.2104],
[-1.6874],
[-0.5222],
[-0.2036]])
In [91]: demeaned = arr - row_means.reshape((4, 1))
In [92]: demeaned.mean(1)
Out[92]: array([ 0., -0., 0., 0.])
圖A-5說明了該運算的過程。
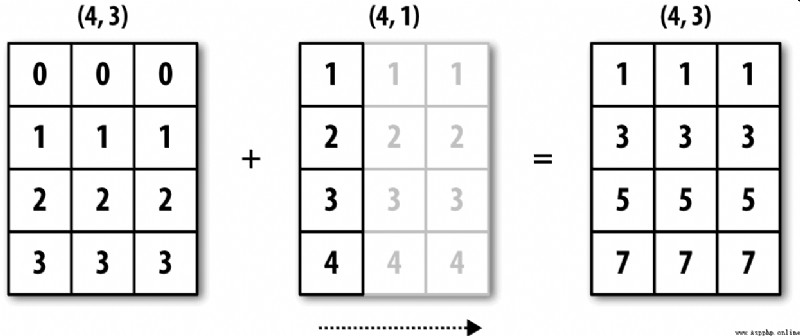
圖A-6展示了另外一種情況,這次是在一個三維數組上沿0軸向加上一個二維數組。
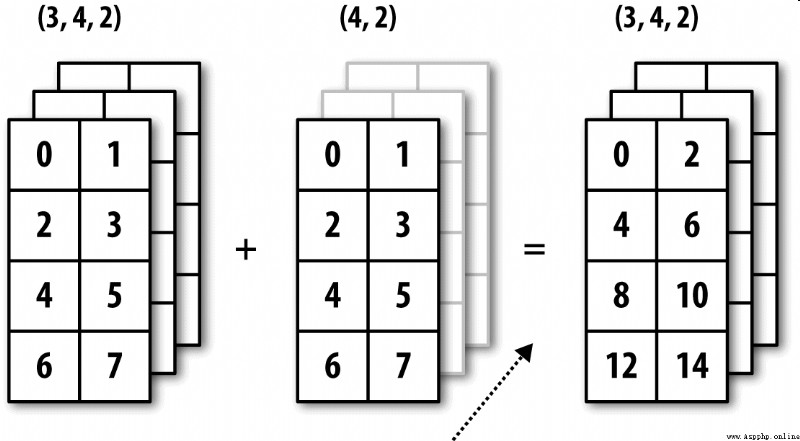
高維度數組的廣播似乎更難以理解,而實際上它也是遵循廣播原則的。如果不然,你就會得到下面這樣一個錯誤:
In [93]: arr - arr.mean(1)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-93-7b87b85a20b2> in <module>()
----> 1 arr - arr.mean(1)
ValueError: operands could not be broadcast together with shapes (4,3) (4,)
人們經常需要通過算術運算過程將較低維度的數組在除0軸以外的其他軸向上廣播。根據廣播的原則,較小數組的“廣播維”必須為1。在上面那個行距平化的例子中,這就意味著要將行平均值的形狀變成(4,1)而不是(4,):
In [94]: arr - arr.mean(1).reshape((4, 1))
Out[94]:
array([[-0.2095, 1.1334, -0.9239],
[ 0.8562, -0.6828, -0.1734],
[-0.3386, 1.0823, -0.7438],
[ 0.3234, -0.8599, 0.5365]])
對於三維的情況,在三維中的任何一維上廣播其實也就是將數據重塑為兼容的形狀而已。圖A-7說明了要在三維數組各維度上廣播的形狀需求。
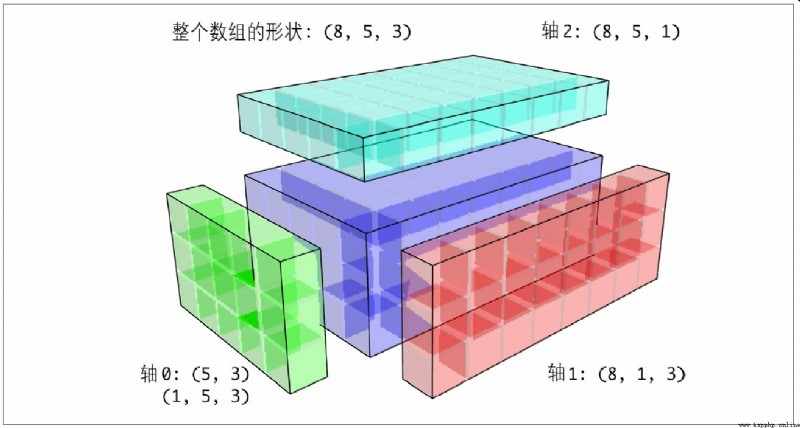
於是就有了一個非常普遍的問題(尤其是在通用算法中),即專門為了廣播而添加一個長度為1的新軸。雖然reshape是一個辦法,但插入軸需要構造一個表示新形狀的元組。這是一個很郁悶的過程。因此,NumPy數組提供了一種通過索引機制插入軸的特殊語法。下面這段代碼通過特殊的np.newaxis屬性以及“全”切片來插入新軸:
In [95]: arr = np.zeros((4, 4))
In [96]: arr_3d = arr[:, np.newaxis, :]
In [97]: arr_3d.shape
Out[97]: (4, 1, 4)
In [98]: arr_1d = np.random.normal(size=3)
In [99]: arr_1d[:, np.newaxis]
Out[99]:
array([[-2.3594],
[-0.1995],
[-1.542 ]])
In [100]: arr_1d[np.newaxis, :]
Out[100]: array([[-2.3594, -0.1995, -1.542 ]])
因此,如果我們有一個三維數組,並希望對軸2進行距平化,那麼只需要編寫下面這樣的代碼就可以了:
In [101]: arr = np.random.randn(3, 4, 5)
In [102]: depth_means = arr.mean(2)
In [103]: depth_means
Out[103]:
array([[-0.4735, 0.3971, -0.0228, 0.2001],
[-0.3521, -0.281 , -0.071 , -0.1586],
[ 0.6245, 0.6047, 0.4396, -0.2846]])
In [104]: depth_means.shape
Out[104]: (3, 4)
In [105]: demeaned = arr - depth_means[:, :, np.newaxis]
In [106]: demeaned.mean(2)
Out[106]:
array([[ 0., 0., -0., -0.],
[ 0., 0., -0., 0.],
[ 0., 0., -0., -0.]])
有些讀者可能會想,在對指定軸進行距平化時,有沒有一種既通用又不犧牲性能的方法呢?實際上是有的,但需要一些索引方面的技巧:
def demean_axis(arr, axis=0):
means = arr.mean(axis)
# This generalizes things like [:, :, np.newaxis] to N dimensions
indexer = [slice(None)] * arr.ndim
indexer[axis] = np.newaxis
return arr - means[indexer]
算術運算所遵循的廣播原則同樣也適用於通過索引機制設置數組值的操作。對於最簡單的情況,我們可以這樣做:
In [107]: arr = np.zeros((4, 3))
In [108]: arr[:] = 5
In [109]: arr
Out[109]:
array([[ 5., 5., 5.],
[ 5., 5., 5.],
[ 5., 5., 5.],
[ 5., 5., 5.]])
但是,假設我們想要用一個一維數組來設置目標數組的各列,只要保證形狀兼容就可以了:
In [110]: col = np.array([1.28, -0.42, 0.44, 1.6])
In [111]: arr[:] = col[:, np.newaxis]
In [112]: arr
Out[112]:
array([[ 1.28, 1.28, 1.28],
[-0.42, -0.42, -0.42],
[ 0.44, 0.44, 0.44],
[ 1.6 , 1.6 , 1.6 ]])
In [113]: arr[:2] = [[-1.37], [0.509]]
In [114]: arr
Out[114]:
array([[-1.37 , -1.37 , -1.37 ],
[ 0.509, 0.509, 0.509],
[ 0.44 , 0.44 , 0.44 ],
[ 1.6 , 1.6 , 1.6 ]])
雖然許多NumPy用戶只會用到通用函數所提供的快速的元素級運算,但通用函數實際上還有一些高級用法能使我們丟開循環而編寫出更為簡潔的代碼。
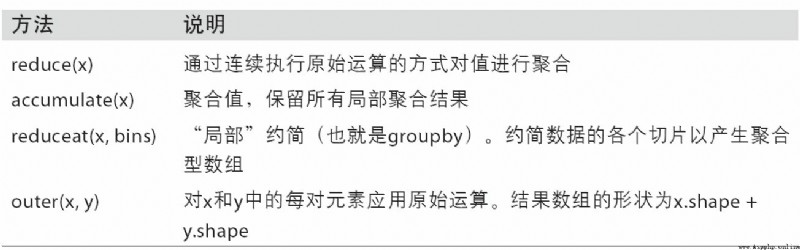
NumPy的各個二元ufunc都有一些用於執行特定矢量化運算的特殊方法。表A-2匯總了這些方法,下面我將通過幾個具體的例子對它們進行說明。
reduce接受一個數組參數,並通過一系列的二元運算對其值進行聚合(可指明軸向)。例如,我們可以用np.add.reduce對數組中各個元素進行求和:
In [115]: arr = np.arange(10)
In [116]: np.add.reduce(arr)
Out[116]: 45
In [117]: arr.sum()
Out[117]: 45
起始值取決於ufunc(對於add的情況,就是0)。如果設置了軸號,約簡運算就會沿該軸向執行。這就使你能用一種比較簡潔的方式得到某些問題的答案。在下面這個例子中,我們用np.logical_and檢查數組各行中的值是否是有序的:
In [118]: np.random.seed(12346) # for reproducibility
In [119]: arr = np.random.randn(5, 5)
In [120]: arr[::2].sort(1) # sort a few rows
In [121]: arr[:, :-1] < arr[:, 1:]
Out[121]:
array([[ True, True, True, True],
[False, True, False, False],
[ True, True, True, True],
[ True, False, True, True],
[ True, True, True, True]], dtype=bool)
In [122]: np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)
Out[122]: array([ True, False, True, False, True], dtype=bool)
注意,logical_and.reduce跟all方法是等價的。
ccumulate跟reduce的關系就像cumsum跟sum的關系那樣。它產生一個跟原數組大小相同的中間“累計”值數組:
In [123]: arr = np.arange(15).reshape((3, 5))
In [124]: np.add.accumulate(arr, axis=1)
Out[124]:
array([[ 0, 1, 3, 6, 10],
[ 5, 11, 18, 26, 35],
[10, 21, 33, 46, 60]])
outer用於計算兩個數組的叉積:
In [125]: arr = np.arange(3).repeat([1, 2, 2])
In [126]: arr
Out[126]: array([0, 1, 1, 2, 2])
In [127]: np.multiply.outer(arr, np.arange(5))
Out[127]:
array([[0, 0, 0, 0, 0],
[0, 1, 2, 3, 4],
[0, 1, 2, 3, 4],
[0, 2, 4, 6, 8],
[0, 2, 4, 6, 8]])
outer輸出結果的維度是兩個輸入數據的維度之和:
In [128]: x, y = np.random.randn(3, 4), np.random.randn(5)
In [129]: result = np.subtract.outer(x, y)
In [130]: result.shape
Out[130]: (3, 4, 5)
最後一個方法reduceat用於計算“局部約簡”,其實就是一個對數據各切片進行聚合的groupby運算。它接受一組用於指示如何對值進行拆分和聚合的“面元邊界”:
In [131]: arr = np.arange(10)
In [132]: np.add.reduceat(arr, [0, 5, 8])
Out[132]: array([10, 18, 17])
最終結果是在arr[0:5]、arr[5:8]以及arr[8:]上執行的約簡。跟其他方法一樣,這裡也可以傳入一個axis參數:
In [133]: arr = np.multiply.outer(np.arange(4), np.arange(5))
In [134]: arr
Out[134]:
array([[ 0, 0, 0, 0, 0],
[ 0, 1, 2, 3, 4],
[ 0, 2, 4, 6, 8],
[ 0, 3, 6, 9, 12]])
In [135]: np.add.reduceat(arr, [0, 2, 4], axis=1)
Out[135]:
array([[ 0, 0, 0],
[ 1, 5, 4],
[ 2, 10, 8],
[ 3, 15, 12]])
表A-2總結了部分的ufunc方法。
有多種方法可以讓你編寫自己的NumPy ufuncs。最常見的是使用NumPy C API,但它超越了本書的范圍。在本節,我們講純粹的Python ufunc。
numpy.frompyfunc接受一個Python函數以及兩個分別表示輸入輸出參數數量的參數。例如,下面是一個能夠實現元素級加法的簡單函數:
In [136]: def add_elements(x, y):
.....: return x + y
In [137]: add_them = np.frompyfunc(add_elements, 2, 1)
In [138]: add_them(np.arange(8), np.arange(8))
Out[138]: array([0, 2, 4, 6, 8, 10, 12, 14], dtype=object)
用frompyfunc創建的函數總是返回Python對象數組,這一點很不方便。幸運的是,還有另一個辦法,即numpy.vectorize。雖然沒有frompyfunc那麼強大,但可以讓你指定輸出類型:
In [139]: add_them = np.vectorize(add_elements, otypes=[np.float64])
In [140]: add_them(np.arange(8), np.arange(8))
Out[140]: array([ 0., 2., 4., 6., 8., 10., 12., 14.])
雖然這兩個函數提供了一種創建ufunc型函數的手段,但它們非常慢,因為它們在計算每個元素時都要執行一次Python函數調用,這就會比NumPy自帶的基於C的ufunc慢很多:
In [141]: arr = np.random.randn(10000)
In [142]: %timeit add_them(arr, arr)
4.12 ms +- 182 us per loop (mean +- std. dev. of 7 runs, 100 loops each)
In [143]: %timeit np.add(arr, arr)
6.89 us +- 504 ns per loop (mean +- std. dev. of 7 runs, 100000 loops each)
本章的後面,我會介紹使用Numba(http://numba.pydata.org/),創建快速Python ufuncs。
你可能已經注意到了,到目前為止我們所討論的ndarray都是一種同質數據容器,也就是說,在它所表示的內存塊中,各元素占用的字節數相同(具體根據dtype而定)。從表面上看,它似乎不能用於表示異質或表格型的數據。結構化數組是一種特殊的ndarray,其中的各個元素可以被看做C語言中的結構體(struct,這就是“結構化”的由來)或SQL表中帶有多個命名字段的行:
In [144]: dtype = [('x', np.float64), ('y', np.int32)]
In [145]: sarr = np.array([(1.5, 6), (np.pi, -2)], dtype=dtype)
In [146]: sarr
Out[146]:
array([( 1.5 , 6), ( 3.1416, -2)],
dtype=[('x', '<f8'), ('y', '<i4')])
定義結構化dtype(請參考NumPy的在線文檔)的方式有很多。最典型的辦法是元組列表,各元組的格式為(field_name,field_data_type)。這樣,數組的元素就成了元組式的對象,該對象中各個元素可以像字典那樣進行訪問:
In [147]: sarr[0]
Out[147]: ( 1.5, 6)
In [148]: sarr[0]['y']
Out[148]: 6
字段名保存在dtype.names屬性中。在訪問結構化數組的某個字段時,返回的是該數據的視圖,所以不會發生數據復制:
In [149]: sarr['x']
Out[149]: array([ 1.5 , 3.1416])
在定義結構化dtype時,你可以再設置一個形狀(可以是一個整數,也可以是一個元組):
In [150]: dtype = [('x', np.int64, 3), ('y', np.int32)]
In [151]: arr = np.zeros(4, dtype=dtype)
In [152]: arr
Out[152]:
array([([0, 0, 0], 0), ([0, 0, 0], 0), ([0, 0, 0], 0), ([0, 0, 0], 0)],
dtype=[('x', '<i8', (3,)), ('y', '<i4')])
在這種情況下,各個記錄的x字段所表示的是一個長度為3的數組:
In [153]: arr[0]['x']
Out[153]: array([0, 0, 0])
這樣,訪問arr[‘x’]即可得到一個二維數組,而不是前面那個例子中的一維數組:
In [154]: arr['x']
Out[154]:
array([[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])
這就使你能用單個數組的內存塊存放復雜的嵌套結構。你還可以嵌套dtype,作出更復雜的結構。下面是一個簡單的例子:
In [155]: dtype = [('x', [('a', 'f8'), ('b', 'f4')]), ('y', np.int32)]
In [156]: data = np.array([((1, 2), 5), ((3, 4), 6)], dtype=dtype)
In [157]: data['x']
Out[157]:
array([( 1., 2.), ( 3., 4.)],
dtype=[('a', '<f8'), ('b', '<f4')])
In [158]: data['y']
Out[158]: array([5, 6], dtype=int32)
In [159]: data['x']['a']
Out[159]: array([ 1., 3.])
pandas的DataFrame並不直接支持該功能,但它的分層索引機制跟這個差不多。
跟pandas的DataFrame相比,NumPy的結構化數組是一種相對較低級的工具。它可以將單個內存塊解釋為帶有任意復雜嵌套列的表格型結構。由於數組中的每個元素在內存中都被表示為固定的字節數,所以結構化數組能夠提供非常快速高效的磁盤數據讀寫(包括內存映像)、網絡傳輸等功能。
結構化數組的另一個常見用法是,將數據文件寫成定長記錄字節流,這是C和C++代碼中常見的數據序列化手段(業界許多歷史系統中都能找得到)。只要知道文件的格式(記錄的大小、元素的順序、字節數以及數據類型等),就可以用np.fromfile將數據讀入內存。這種用法超出了本書的范圍,知道這點就可以了。
跟Python內置的列表一樣,ndarray的sort實例方法也是就地排序。也就是說,數組內容的重新排列是不會產生新數組的:
In [160]: arr = np.random.randn(6)
In [161]: arr.sort()
In [162]: arr
Out[162]: array([-1.082 , 0.3759, 0.8014, 1.1397, 1.2888, 1.8413])
在對數組進行就地排序時要注意一點,如果目標數組只是一個視圖,則原始數組將會被修改:
In [163]: arr = np.random.randn(3, 5)
In [164]: arr
Out[164]:
array([[-0.3318, -1.4711, 0.8705, -0.0847, -1.1329],
[-1.0111, -0.3436, 2.1714, 0.1234, -0.0189],
[ 0.1773, 0.7424, 0.8548, 1.038 , -0.329 ]])
In [165]: arr[:, 0].sort() # Sort first column values in-place
In [166]: arr
Out[166]:
array([[-1.0111, -1.4711, 0.8705, -0.0847, -1.1329],
[-0.3318, -0.3436, 2.1714, 0.1234, -0.0189],
[ 0.1773, 0.7424, 0.8548, 1.038 , -0.329 ]])
相反,numpy.sort會為原數組創建一個已排序副本。另外,它所接受的參數(比如kind)跟ndarray.sort一樣:
In [167]: arr = np.random.randn(5)
In [168]: arr
Out[168]: array([-1.1181, -0.2415, -2.0051, 0.7379, -1.0614])
In [169]: np.sort(arr)
Out[169]: array([-2.0051, -1.1181, -1.0614, -0.2415, 0.7379])
In [170]: arr
Out[170]: array([-1.1181, -0.2415, -2.0051, 0.7379, -1.0614])
這兩個排序方法都可以接受一個axis參數,以便沿指定軸向對各塊數據進行單獨排序:
In [171]: arr = np.random.randn(3, 5)
In [172]: arr
Out[172]:
array([[ 0.5955, -0.2682, 1.3389, -0.1872, 0.9111],
[-0.3215, 1.0054, -0.5168, 1.1925, -0.1989],
[ 0.3969, -1.7638, 0.6071, -0.2222, -0.2171]])
In [173]: arr.sort(axis=1)
In [174]: arr
Out[174]:
array([[-0.2682, -0.1872, 0.5955, 0.9111, 1.3389],
[-0.5168, -0.3215, -0.1989, 1.0054, 1.1925],
[-1.7638, -0.2222, -0.2171, 0.3969, 0.6071]])
你可能注意到了,這兩個排序方法都不可以被設置為降序。其實這也無所謂,因為數組切片會產生視圖(也就是說,不會產生副本,也不需要任何其他的計算工作)。許多Python用戶都很熟悉一個有關列表的小技巧:values[::-1]可以返回一個反序的列表。對ndarray也是如此:
In [175]: arr[:, ::-1]
Out[175]:
array([[ 1.3389, 0.9111, 0.5955, -0.1872, -0.2682],
[ 1.1925, 1.0054, -0.1989, -0.3215, -0.5168],
[ 0.6071, 0.3969, -0.2171, -0.2222, -1.7638]])
在數據分析工作中,常常需要根據一個或多個鍵對數據集進行排序。例如,一個有關學生信息的數據表可能需要以姓和名進行排序(先姓後名)。這就是間接排序的一個例子,如果你閱讀過有關pandas的章節,那就已經見過不少高級例子了。給定一個或多個鍵,你就可以得到一個由整數組成的索引數組(我親切地稱之為索引器),其中的索引值說明了數據在新順序下的位置。argsort和numpy.lexsort就是實現該功能的兩個主要方法。下面是一個簡單的例子:
In [176]: values = np.array([5, 0, 1, 3, 2])
In [177]: indexer = values.argsort()
In [178]: indexer
Out[178]: array([1, 2, 4, 3, 0])
In [179]: values[indexer]
Out[179]: array([0, 1, 2, 3, 5])
一個更復雜的例子,下面這段代碼根據數組的第一行對其進行排序:
In [180]: arr = np.random.randn(3, 5)
In [181]: arr[0] = values
In [182]: arr
Out[182]:
array([[ 5. , 0. , 1. , 3. , 2. ],
[-0.3636, -0.1378, 2.1777, -0.4728, 0.8356],
[-0.2089, 0.2316, 0.728 , -1.3918, 1.9956]])
In [183]: arr[:, arr[0].argsort()]
Out[183]:
array([[ 0. , 1. , 2. , 3. , 5. ],
[-0.1378, 2.1777, 0.8356, -0.4728, -0.3636],
[ 0.2316, 0.728 , 1.9956, -1.3918, -0.2089]])
lexsort跟argsort差不多,只不過它可以一次性對多個鍵數組執行間接排序(字典序)。假設我們想對一些以姓和名標識的數據進行排序:
In [184]: first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
In [185]: last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
In [186]: sorter = np.lexsort((first_name, last_name))
In [187]: sorter
Out[187]: array([1, 2, 3, 0, 4])
In [188]: zip(last_name[sorter], first_name[sorter])
Out[188]: <zip at 0x7fa203eda1c8>
剛開始使用lexsort的時候可能會比較容易頭暈,這是因為鍵的應用順序是從最後一個傳入的算起的。不難看出,last_name是先於first_name被應用的。
筆記:Series和DataFrame的sort_index以及Series的order方法就是通過這些函數的變體(它們還必須考慮缺失值)實現的。
穩定的(stable)排序算法會保持等價元素的相對位置。對於相對位置具有實際意義的那些間接排序而言,這一點非常重要:
In [189]: values = np.array(['2:first', '2:second', '1:first', '1:second',
.....: '1:third'])
In [190]: key = np.array([2, 2, 1, 1, 1])
In [191]: indexer = key.argsort(kind='mergesort')
In [192]: indexer
Out[192]: array([2, 3, 4, 0, 1])
In [193]: values.take(indexer)
Out[193]:
array(['1:first', '1:second', '1:third', '2:first', '2:second'],
dtype='<U8')
mergesort(合並排序)是唯一的穩定排序,它保證有O(n log n)的性能(空間復雜度),但是其平均性能比默認的quicksort(快速排序)要差。表A-3列出了可用的排序算法及其相關的性能指標。大部分用戶完全不需要知道這些東西,但了解一下總是好的。

排序的目的之一可能是確定數組中最大或最小的元素。NumPy有兩個優化方法,numpy.partition和np.argpartition,可以在第k個最小元素劃分的數組:
In [194]: np.random.seed(12345)
In [195]: arr = np.random.randn(20)
In [196]: arr
Out[196]:
array([-0.2047, 0.4789, -0.5194, -0.5557, 1.9658, 1.3934, 0.0929,
0.2817, 0.769 , 1.2464, 1.0072, -1.2962, 0.275 , 0.2289,
1.3529, 0.8864, -2.0016, -0.3718, 1.669 , -0.4386])
In [197]: np.partition(arr, 3)
Out[197]:
array([-2.0016, -1.2962, -0.5557, -0.5194, -0.3718, -0.4386, -0.2047,
0.2817, 0.769 , 0.4789, 1.0072, 0.0929, 0.275 , 0.2289,
1.3529, 0.8864, 1.3934, 1.9658, 1.669 , 1.2464])
當你調用partition(arr, 3),結果中的頭三個元素是最小的三個,沒有特定的順序。numpy.argpartition與numpy.argsort相似,會返回索引,重排數據為等價的順序:
In [198]: indices = np.argpartition(arr, 3)
In [199]: indices
Out[199]:
array([16, 11, 3, 2, 17, 19, 0, 7, 8, 1, 10, 6, 12, 13, 14, 15, 5,
4, 18, 9])
In [200]: arr.take(indices)
Out[200]:
array([-2.0016, -1.2962, -0.5557, -0.5194, -0.3718, -0.4386, -0.2047,
0.2817, 0.769 , 0.4789, 1.0072, 0.0929, 0.275 , 0.2289,
1.3529, 0.8864, 1.3934, 1.9658, 1.669 , 1.2464])
searchsorted是一個在有序數組上執行二分查找的數組方法,只要將值插入到它返回的那個位置就能維持數組的有序性:
In [201]: arr = np.array([0, 1, 7, 12, 15])
In [202]: arr.searchsorted(9)
Out[202]: 3
你可以傳入一組值就能得到一組索引:
In [203]: arr.searchsorted([0, 8, 11, 16])
Out[203]: array([0, 3, 3, 5])
從上面的結果中可以看出,對於元素0,searchsorted會返回0。這是因為其默認行為是返回相等值組的左側索引:
In [204]: arr = np.array([0, 0, 0, 1, 1, 1, 1])
In [205]: arr.searchsorted([0, 1])
Out[205]: array([0, 3])
In [206]: arr.searchsorted([0, 1], side='right')
Out[206]: array([3, 7])
再來看searchsorted的另一個用法,假設我們有一個數據數組(其中的值在0到10000之間),還有一個表示“面元邊界”的數組,我們希望用它將數據數組拆分開:
In [207]: data = np.floor(np.random.uniform(0, 10000, size=50))
In [208]: bins = np.array([0, 100, 1000, 5000, 10000])
In [209]: data
Out[209]:
array([ 9940., 6768., 7908., 1709., 268., 8003., 9037., 246.,
4917., 5262., 5963., 519., 8950., 7282., 8183., 5002.,
8101., 959., 2189., 2587., 4681., 4593., 7095., 1780.,
5314., 1677., 7688., 9281., 6094., 1501., 4896., 3773.,
8486., 9110., 3838., 3154., 5683., 1878., 1258., 6875.,
7996., 5735., 9732., 6340., 8884., 4954., 3516., 7142.,
5039., 2256.])
然後,為了得到各數據點所屬區間的編號(其中1表示面元[0,100)),我們可以直接使用searchsorted:
In [210]: labels = bins.searchsorted(data)
In [211]: labels
Out[211]:
array([4, 4, 4, 3, 2, 4, 4, 2, 3, 4, 4, 2, 4, 4, 4, 4, 4, 2, 3, 3, 3, 3, 4,
3, 4, 3, 4, 4, 4, 3, 3, 3, 4, 4, 3, 3, 4, 3, 3, 4, 4, 4, 4, 4, 4, 3,
3, 4, 4, 3])
通過pandas的groupby使用該結果即可非常輕松地對原數據集進行拆分:
In [212]: pd.Series(data).groupby(labels).mean()
Out[212]:
2 498.000000
3 3064.277778
4 7389.035714
dtype: float64
#A.7 用Numba編寫快速NumPy函數
Numba是一個開源項目,它可以利用CPUs、GPUs或其它硬件為類似NumPy的數據創建快速函數。它使用了LLVM項目(http://llvm.org/),將Python代碼轉換為機器代碼。
為了介紹Numba,來考慮一個純粹的Python函數,它使用for循環計算表達式(x - y).mean():
import numpy as np
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
這個函數很慢:
In [209]: x = np.random.randn(10000000)
In [210]: y = np.random.randn(10000000)
In [211]: %timeit mean_distance(x, y)
1 loop, best of 3: 2 s per loop
In [212]: %timeit (x - y).mean()
100 loops, best of 3: 14.7 ms per loop
NumPy的版本要比它快過100倍。我們可以轉換這個函數為編譯的Numba函數,使用numba.jit函數:
In [213]: import numba as nb
In [214]: numba_mean_distance = nb.jit(mean_distance)
也可以寫成裝飾器:
@nb.jit
def mean_distance(x, y):
nx = len(x)
result = 0.0
count = 0
for i in range(nx):
result += x[i] - y[i]
count += 1
return result / count
它要比矢量化的NumPy快:
In [215]: %timeit numba_mean_distance(x, y)
100 loops, best of 3: 10.3 ms per loop
Numba不能編譯Python代碼,但它支持純Python寫的一個部分,可以編寫數值算法。
Numba是一個深厚的庫,支持多種硬件、編譯模式和用戶插件。它還可以編譯NumPy Python API的一部分,而不用for循環。Numba也可以識別可以便以為機器編碼的結構體,但是若調用CPython API,它就不知道如何編譯。Numba的jit函數有一個選項,nopython=True,它限制了可以被轉換為Python代碼的代碼,這些代碼可以編譯為LLVM,但沒有任何Python C API調用。jit(nopython=True)有一個簡短的別名numba.njit。
前面的例子,我們還可以這樣寫:
from numba import float64, njit
@njit(float64(float64[:], float64[:]))
def mean_distance(x, y):
return (x - y).mean()
我建議你學習Numba的線上文檔(http://numba.pydata.org/)。下一節介紹一個創建自定義Numpy ufunc對象的例子。
numba.vectorize創建了一個編譯的NumPy ufunc,它與內置的ufunc很像。考慮一個numpy.add的Python例子:
from numba import vectorize
@vectorize
def nb_add(x, y):
return x + y
現在有:
In [13]: x = np.arange(10)
In [14]: nb_add(x, x)
Out[14]: array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18.])
In [15]: nb_add.accumulate(x, 0)
Out[15]: array([ 0., 1., 3., 6., 10., 15., 21., 28., 36., 45.])
我在第4章中講過,np.save和np.load可用於讀寫磁盤上以二進制格式存儲的數組。其實還有一些工具可用於更為復雜的場景。尤其是內存映像(memory map),它使你能處理在內存中放不下的數據集。
內存映像文件是一種將磁盤上的非常大的二進制數據文件當做內存中的數組進行處理的方式。NumPy實現了一個類似於ndarray的memmap對象,它允許將大文件分成小段進行讀寫,而不是一次性將整個數組讀入內存。另外,memmap也擁有跟普通數組一樣的方法,因此,基本上只要是能用於ndarray的算法就也能用於memmap。
要創建一個內存映像,可以使用函數np.memmap並傳入一個文件路徑、數據類型、形狀以及文件模式:
In [214]: mmap = np.memmap('mymmap', dtype='float64', mode='w+',
.....: shape=(10000, 10000))
In [215]: mmap
Out[215]:
memmap([[ 0., 0., 0., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 0., 0., 0.],
...,
[ 0., 0., 0., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 0., 0., 0.]])
對memmap切片將會返回磁盤上的數據的視圖:
In [216]: section = mmap[:5]
如果將數據賦值給這些視圖:數據會先被緩存在內存中(就像是Python的文件對象),調用flush即可將其寫入磁盤:
In [217]: section[:] = np.random.randn(5, 10000)
In [218]: mmap.flush()
In [219]: mmap
Out[219]:
memmap([[ 0.7584, -0.6605, 0.8626, ..., 0.6046, -0.6212, 2.0542],
[-1.2113, -1.0375, 0.7093, ..., -1.4117, -0.1719, -0.8957],
[-0.1419, -0.3375, 0.4329, ..., 1.2914, -0.752 , -0.44 ],
...,
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ]])
In [220]: del mmap
只要某個內存映像超出了作用域,它就會被垃圾回收器回收,之前對其所做的任何修改都會被寫入磁盤。當打開一個已經存在的內存映像時,仍然需要指明數據類型和形狀,因為磁盤上的那個文件只是一塊二進制數據而已,沒有任何元數據:
In [221]: mmap = np.memmap('mymmap', dtype='float64', shape=(10000, 10000))
In [222]: mmap
Out[222]:
memmap([[ 0.7584, -0.6605, 0.8626, ..., 0.6046, -0.6212, 2.0542],
[-1.2113, -1.0375, 0.7093, ..., -1.4117, -0.1719, -0.8957],
[-0.1419, -0.3375, 0.4329, ..., 1.2914, -0.752 , -0.44 ],
...,
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ]])
內存映像可以使用前面介紹的結構化或嵌套dtype。
PyTables和h5py這兩個Python項目可以將NumPy的數組數據存儲為高效且可壓縮的HDF5格式(HDF意思是“層次化數據格式”)。你可以安全地將好幾百GB甚至TB的數據存儲為HDF5格式。要學習Python使用HDF5,請參考pandas線上文檔。
使用NumPy的代碼的性能一般都很不錯,因為數組運算一般都比純Python循環快得多。下面大致列出了一些需要注意的事項:
如果單用NumPy無論如何都達不到所需的性能指標,就可以考慮一下用C、Fortran或Cython(等下會稍微介紹一下)來編寫代碼。我自己在工作中經常會用到Cython(http://cython.org),因為它不用花費我太多精力就能得到C語言那樣的性能。
雖然這個話題有點超出本書的范圍,但還是要提一下,因為在某些應用場景中,數組的內存布局可以對計算速度造成極大的影響。這是因為性能差別在一定程度上跟CPU的高速緩存(cache)體系有關。運算過程中訪問連續內存塊(例如,對以C順序存儲的數組的行求和)一般是最快的,因為內存子系統會將適當的內存塊緩存到超高速的L1或L2CPU Cache中。此外,NumPy的C語言基礎代碼(某些)對連續存儲的情況進行了優化處理,這樣就能避免一些跨越式的內存訪問。
一個數組的內存布局是連續的,就是說元素是以它們在數組中出現的順序(即Fortran型(列優先)或C型(行優先))存儲在內存中的。默認情況下,NumPy數組是以C型連續的方式創建的。列優先的數組(比如C型連續數組的轉置)也被稱為Fortran型連續。通過ndarray的flags屬性即可查看這些信息:
In [225]: arr_c = np.ones((1000, 1000), order='C')
In [226]: arr_f = np.ones((1000, 1000), order='F')
In [227]: arr_c.flags
Out[227]:
C_CONTIGUOUS : True
F_CONTIGUOUS : False
OWNDATA : True
WRITEABLE : True
ALIGNED : True
UPDATEIFCOPY : False
In [228]: arr_f.flags
Out[228]:
C_CONTIGUOUS : False
F_CONTIGUOUS : True
OWNDATA : True
WRITEABLE : True
ALIGNED : True
UPDATEIFCOPY : False
In [229]: arr_f.flags.f_contiguous
Out[229]: True
在這個例子中,對兩個數組的行進行求和計算,理論上說,arr_c會比arr_f快,因為arr_c的行在內存中是連續的。我們可以在IPython中用%timeit來確認一下:
In [230]: %timeit arr_c.sum(1)
784 us +- 10.4 us per loop (mean +- std. dev. of 7 runs, 1000 loops each)
In [231]: %timeit arr_f.sum(1)
934 us +- 29 us per loop (mean +- std. dev. of 7 runs, 1000 loops each)
如果想從NumPy中提升性能,這裡就應該是下手的地方。如果數組的內存順序不符合你的要求,使用copy並傳入’C’或’F’即可解決該問題:
In [232]: arr_f.copy('C').flags
Out[232]:
C_CONTIGUOUS : True
F_CONTIGUOUS : False
OWNDATA : True
WRITEABLE : True
ALIGNED : True
UPDATEIFCOPY : False
注意,在構造數組的視圖時,其結果不一定是連續的:
In [233]: arr_c[:50].flags.contiguous
Out[233]: True
In [234]: arr_c[:, :50].flags
Out[234]:
C_CONTIGUOUS : False
F_CONTIGUOUS : False
OWNDATA : False
WRITEABLE : True
ALIGNED : True
UPDATEIFCOPY : False