First , Thank you very much b standing up The Lord is for Dijkstra Introduction of algorithm , Benefited greatly , The video link about this algorithm is here
「Python Study 」 Implement Dijstra algorithm and generate the shortest path _ Bili, Bili _bilibili
I am also following this up Only then did the master slowly understand the details of this algorithm . below , This article is about Dijksta The algorithm is explained and python Code implementation and case analysis .
Catalog
background
Code and explanation
Third party library solutions
Case study —— Device update problem
summary
The shortest path algorithm can not only solve the shortest path between any two locations , It can also solve problems such as pipe laying 、 Line safety 、 Factory layout 、 Equipment update, etc .
I won't talk about graph theory here , It's a little complicated , On the basis of understanding this article , Let's talk about how to understand the following figure first
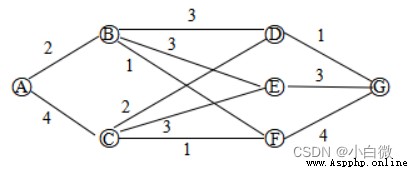
You can see , Some points on the graph are directly connected , Some don't . For direct connected , Such as A To B, There are marks on the line 2, That is to say A To B Distance of , But for the A To C, This kind of point without direct connection , Remember that its distance is infinite . A node is a point on a graph . The example graph used in this paper is an undirected graph , That is to say, you can start from A To B, You can also get it from B To A. For a directed graph, that is to say, it can only go in the direction of the arrow , You can't go back , The distance is infinite .
This paper mainly talks about the shortest path algorithm Dijksta Algorithm , It is applicable to the case that the right of way is not negative . The specific steps to simplify the understanding are ( Personal understanding , Such as incorrect , You are welcome to criticize and correct ):
1. First determine the starting point , The distance between the starting point and the starting point is 0
2. Determine the destination , Find all the paths from the starting point to the ending point
3. By iteration , Find the shortest distance from the starting point to the end point , And mark it
At first glance , It's simple , However , Not really , If there are many intermediate points between the start point and the end point , It is difficult to calculate manually . below , adopt python To implement such three steps as the above .
The above picture is an example , The matrix we enter is network, That is, the adjacency matrix , This matrix is a square matrix . The data in the first row and the first column is A From A Distance of . But the zero in it doesn't necessarily mean the distance from yourself , For example, the first row and the fifth column , Express A To E There is no direct connection , This may be somewhat contradictory to what I said above , But the algorithm doesn't really run on this matrix , So leave it alone . Observe carefully , It can be found that this matrix is symmetric , Of course , It is also limited to undirected graphs .
Defined function ,s As the starting point ,d End point
path It's an empty list , Used to store the shortest path from a point to a point , As you can see from here s To d What points does the shortest path of go through .
n Is the number of nodes .
about fmax, quote numpy In the library inf, It means infinity .
w And input matrix constructed for network Of the same dimension 0 matrix , Used for algorithm operation .
book For a list , The number of elements is the number of nodes , Its function is , When the minimum distance from a point to a point has been determined , marked , If there are other paths including this path , The calculation of the program can be reduced .
dis For the final returned path list , Represents the minimum path from a point to a point , Altogether n individual .
minpath Store the nodes that will pass from a point to a point .path It determines the nodes in the .
import numpy as np
network = np.array([[0,2,4,0,0,0,0],
[2,0,0,3,3,1,0],
[4,0,0,2,3,1,0],
[0,3,2,0,0,0,1],
[0,3,3,0,0,0,3],
[0,1,1,0,0,0,4],
[0,0,0,1,3,4,0]])
def Dijkstra(network,s,d): # Dijestra algorithm calculates s To t Shortest path , And return the path and distance
print("Start Dijstra Path……")
path = [] # Store s To d Shortest path
n = len(network) # Number of nodes
fmax = np.inf
w = [[0 for i in range(n)] for j in range(n)]
book = [0 for i in range(n)] # Is it already the smallest tag list
dis = [fmax for i in range(n)] # s Minimum distance to other nodes
book[s-1] = 1 # Node number from 1 Start , The serial number of the list is from 0 Start
midpath = [-1 for i in range(n)] # Previous jump list This step is to w Matrix initialization , Become a standard matrix that the program can handle , After processing the w Direct link or itself fmax. about i=s-1, In fact, it is because the serial number of the list is from 0 At the beginning , And our habit is from 1 Start
''' This loop converts the 0 The price is fmax, And think that direct connection is the shortest ( But that's not the case )'''
for i in range(n):
for j in range(n):
if network[i][j] != 0:
w[i][j] = network[i][j] # 0→max
else:
w[i][j] = fmax
if i == s-1 and network[i][j] != 0: # The minimum distance between directly connected nodes is network[i][j]
dis[j] = network[i][j]Next is the main part of the algorithm ,n-1 The second cycle is except s Other nodes besides the nodes of ,for First in the loop min It will be updated , Until you find the shortest distance , Its function is to if In judgment , Check whether the distance is less than min, If so , Yes min updated , Otherwise, use u For recording , Mark the point where the minimum path has been found .dis The original elements are all fmax, Update the elements through iteration , At this time, through this for The result of the loop is not the smallest , After the next cycle . however , The final result is the minimum path . for example dis Output is [inf, 2, 4, 5, 5, 3, 6], It means starting from the first point , The minimum distance from each point in turn .
The next one is v Traversal for elements for In circulation , This step is used to compare whether the direct connection is the shortest , If not , Then change to another one , At the same time minpath Update the list . At this point, the shortest distance has been updated , The next step is to get the path .
j=d-1 And the above i equally , Because of different habits .
''' Algorithm body '''
for i in range(n-1): # n-1 Time to traverse the , except s node
min = fmax # min The value of is always changing
for j in range(n):
if book[j] == 0 and dis[j] < min: # If not traversed and the distance is the smallest , The shortest distance is obtained by repeated comparison
min = dis[j]
u = j
book[u] = 1 # Mark the nodes that have arrived
# u In a circulatory system , from 2 To 7 Traverse
for v in range(1,n): # u Traverse the directly connected nodes
''' Key steps , Used to compare the length of the node directly connected to this node '''
if dis[v] > dis[u] + w[u][v]:
dis[v] = dis[u] + w[u][v]
midpath[v] = u+1 # Last hop update
j = d-1 # j It's the serial number
path.append(d) # Because it stores the last hop , So add the destination node first d, Last but not least In this cycle , It's just s To d Shortest path , Does not include other points between .
For the back one reverse Method , From above path add to d We can know , Need to transpose , Otherwise, it is the opposite
while midpath[j] != -1:
path.append(midpath[j])
j = midpath[j]-1
path.append(s)
path.reverse() # Inverted list
print('path:',path)
print(dis)thus , The algorithm is finished , Next , Just call this function , For testing A To G One of the most short circuit , namely 1 To 7.
Dijkstra(network,1,7)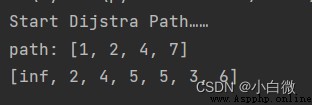
The result shows , from A To G The shortest distance is 6, Path is A—B—D—G. It is still a little difficult to understand the whole algorithm completely ( The boss avoids hey hey ), You can watch the following repeatedly , The complete code is given below , Convenient for observation .
import numpy as np
def Dijkstra(network,s,d): # Dijestra algorithm calculates s To t Shortest path , And return the path and cost
print("Start Dijstra Path……")
path = [] # Store s To t Shortest path
n = len(network) # Number of nodes
fmax = np.inf
w = [[0 for i in range(n)] for j in range(n)]
book = [0 for i in range(n)] # Is it already the smallest tag list
dis = [fmax for i in range(n)] # s Minimum distance to other nodes
book[s-1] = 1 # Node number from 1 Start , The serial number of the list is from 0 Start
midpath = [-1 for i in range(n)] # Previous jump list
# This step can be omitted , Just enter the matrix specification
''' This loop converts the 0 The price is fmax, And think that direct connection is the shortest ( But that's not the case )'''
for i in range(n):
for j in range(n):
if network[i][j] != 0:
w[i][j] = network[i][j] # 0→max
else:
w[i][j] = fmax
if i == s-1 and network[i][j] != 0: # The minimum distance between directly connected nodes is network[i][j]
dis[j] = network[i][j]
# print('dis:',dis)
''' Algorithm body '''
for i in range(n-1): # n-1 Time to traverse the , except s node
min = fmax # min The value of is always changing
for j in range(n):
if book[j] == 0 and dis[j] < min: # If not traversed and the distance is the smallest , The shortest distance is obtained by repeated comparison
min = dis[j]
u = j
# print('book:',book)
book[u] = 1 # Mark the nodes that have arrived
# print('u:',u)
# print('dis:',dis)
# u In a circulatory system , from 2 To 7 Traverse
for v in range(1,n): # u Traverse the directly connected nodes
''' Key steps , Used to compare the length of the node directly connected to this node '''
if dis[v] > dis[u] + w[u][v]:
dis[v] = dis[u] + w[u][v]
midpath[v] = u+1 # Last hop update
j = d-1 # j It's the serial number
path.append(d) # Because it stores the last hop , So add the destination node first d, Last but not least
while midpath[j] != -1:
path.append(midpath[j])
j = midpath[j]-1
path.append(s)
path.reverse() # Inverted list
print('path:',path)
print(midpath)
print(dis)
network = np.array([[0,2,4,0,0,0,0],
[2,0,0,3,3,1,0],
[4,0,0,2,3,1,0],
[0,3,2,0,0,0,1],
[0,3,3,0,0,0,3],
[0,1,1,0,0,0,4],
[0,0,0,1,3,4,0]])
Dijkstra(network,1,7)
If you really don't understand the above code , But I want to use this method , Here is the solution of the third-party library , Use networkx library , Because I don't know much about this library , At present, I only know that this library can draw such diagrams , And with Dijkstra Algorithm for the shortest path , Maximum flow problem . Next, use the code , Let me introduce the following method to you
import networkx as nx
dis = [(0,1,2),(0,2,4),(1,3,3),(1,4,3),(1,5,1),(2,3,2),(2,4,3),(2,5,1),(3,6,1),
(4,6,3),(5,6,4)]
g = nx.Graph()
g.add_weighted_edges_from(dis)
a = nx.to_numpy_matrix(g,nodelist=range(7))
p = nx.dijkstra_path(g,source=0,target=6,weight='weight')
d = nx.dijkstra_path_length(g,0,6,weight='weight')
print(' The shortest path is p={}, The shortest distance is d={}'.format(p,d))
Use the same example above , But by contrast , A lot less code . A brief introduction .
first dis It's a list ,(0,1,2) From A To B The distance to 2,, And so on .
g To initialize a graph ,Graph Represents the generation of an undirected graph .
Next, add nodes and row for the graph , Parameter is dis
a Corresponding to the generated adjacency matrix .
p Use Dijkstra The algorithm gets the shortest path ,d Get the shortest distance .

It can be seen that , The result is consistent with the above code algorithm , But look at that p list , All elements can be +1, That is, the result is consistent with the above code .
Now let's practice with one question , Although it is different from the shortest path between a certain point and a certain point , But the essence is the same . But I just tried this question , There is no guarantee that , So you can think about , I hope I can enlighten you .
An enterprise will 5 One machine will be used within the year , The annual purchase and maintenance cost of this kind of machine ( It is related to the working age of the machine ) As shown in the following table . Try to make a plan for machine purchase and renewal , send 5 Minimum cost in the year .
year
1
2
3
4
5
Purchase cost
Maintenance costs
11
5
11
6
12
8
12
11
13
18
That's what I think :
Make  It means the first one i At the beginning of the year, it was purchased and used till the end of the year j-1 All expenses included at the end of the year , here wij Including the i The annual purchase cost and j-i Annual maintenance cost , So we know
It means the first one i At the beginning of the year, it was purchased and used till the end of the year j-1 All expenses included at the end of the year , here wij Including the i The annual purchase cost and j-i Annual maintenance cost , So we know
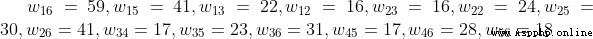
use networkx The library draws the corresponding graph , As shown below :
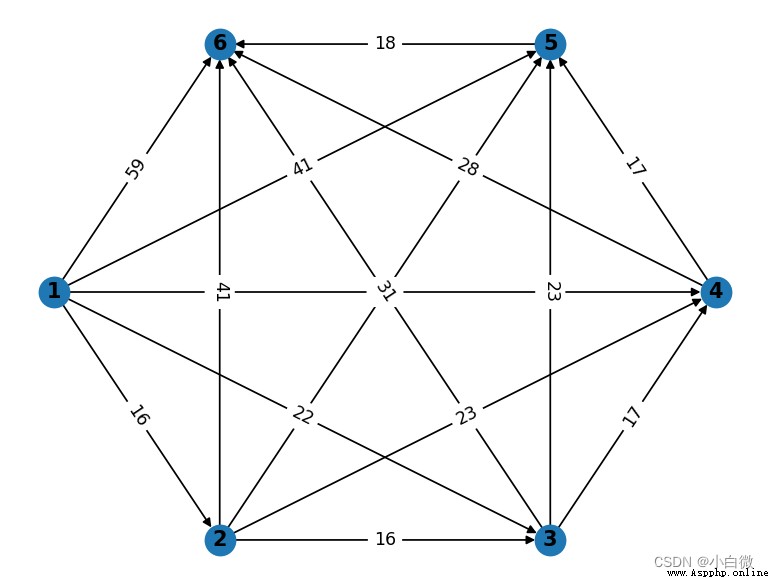
Finally, it is solved by code , From the first year of purchase to the third year , Then buy in the third year and use it at the end of the fifth year , Minimize costs , by 53 Company . Here's the code
import networkx as nx
import numpy as np
import pylab as plt
dis = [(1,5,41),(1,4,30),(1,3,22),(1,2,16),(1,6,59),(2,3,16),
(2,4,23),(2,5,30),(2,6,41),(3,4,17),(3,5,23),(3,6,31),
(4,5,17),(4,6,28),(5,6,18)]
g = nx.DiGraph()
g.add_nodes_from(range(1,7))
g.add_weighted_edges_from(dis)
pos = nx.shell_layout(g)
w = nx.get_edge_attributes(g,'weight')
nx.draw(g,pos,with_labels=True,font_weight='bold',font_size=12)
nx.draw_networkx_edge_labels(g,pos,edge_labels=w)
plt.show()
a = nx.to_numpy_matrix(g,nodelist=range(1,7))
p = nx.dijkstra_path(g,source=1,target=6,weight='weight')
d = nx.dijkstra_path_length(g,1,6,weight='weight')
print(p,d,sep='\n')g.add_nodes_from Indicates adding nodes ,g.add_weighted_edges_from It means to increase the right of way , Parameter bit dis,pos Is a parameter for drawing , Code from w Start to plt.show It's all for drawing ( If not required , You can ignore ). The following is consistent with the above example , use Dijkstra Algorithmic solution .
It is difficult to use the algorithm step by step , The so-called algorithm is what people think , The program is what the code thinks , The key is how to make the computer understand your idea , But this Dijkstra It is convenient to have a ready-made library for the algorithm , Of course, don't just limit yourself to finding the shortest distance from a certain point to a certain point , It can be extended to , Reach a true understanding .
Algorithm , Still need more practice . For the above code and algorithm explanation , If there is something wrong , You are welcome to criticize and correct . There's something I don't understand , You can also comment on it or send me a private message directly .
It's not easy to create , Thank you for the compliment —— Collection —— Focus on !!!