首先，非常感謝b站up主對於Dijkstra算法的介紹，受益匪淺，關於這個算法的視頻鏈接在這

                   「Python學習」實現迪傑斯特拉算法並生成最短路徑_哔哩哔哩_bilibili

        我也是跟著這位up主才算慢慢懂了這個算法的具體情況。下面，本文就關於Dijksta算法進行相關解釋以及python代碼實現和案例分析。

目錄

背景

代碼及解釋

 第三方庫解決方法

案例——設備更新問題

總結

背景

        最短路算法不僅可以解決任意兩個地點之間的最短路徑，還可以解決諸如管道鋪設、線路安全、工廠布局、設備更新等問題。

        這裡就不講關於圖論的一些東西，講起來有點復雜，在能理解本文的基礎上，給大家先說一下如何去理解下面這個圖

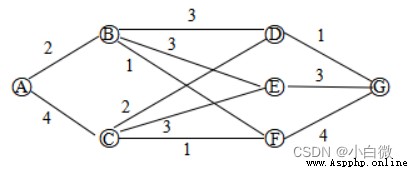
        可以看到，圖上有些點是直接連接的，有些是沒有。對於直連的，如A到B，線上有標注2，即為A到B的距離，但對於A到C，這種沒有直接連接的點，記它的距離為無窮大。節點即圖上的點。本文使用的例圖為無向圖，即表示可以從A到B，也可以從B到A。對於有向圖的即表示只能順著箭頭方向走，不能往回走，距離也就為無窮大。

        本文主要講最短路算法中的Dijksta算法，它適用於路權非負的情況。具體步驟簡化理解大概就是（個人理解，如有誤，歡迎大佬批評指正）：

        1.先確定起始點，起始點與起始點之間的距離為0

        2.確定終點，找出起始點能到達終點的全部路徑

        3.通過迭代，找出起始點到終點的最短距離，並對它進行標記

        乍一看，很簡單，然而，並不然，如果起始點與終點之間存在很多中間點時，就很難通過人工計算。下面，通過python去實現諸如上述三個步驟。

代碼及解釋

       以上圖為例子， 我們輸入的矩陣就是network，也就是常說的鄰接矩陣，這個矩陣為方陣。第一行第一列的數據為A到自A的距離。但裡面的零並不一定表示自己到自己的距離，例如第一行第五列，表示A到E是沒有直連的，這可能跟我上面說的無窮有些矛盾，不過算法真正運行的不是這個矩陣，所以先不用管。仔細觀察，可以發現這個矩陣是對稱的，當然，也僅限於無向圖。

        定義函數，s為起始點，d為終點

        path是一個空列表，用於儲存從某點到某點的最短路徑，從這裡看出s到d的最短路徑需要經過哪些點。

        n為節點個數。

        對於fmax，引用numpy庫中的inf，意味無窮大。

        w為構造的與輸入矩陣network同樣維數的0矩陣，用於算法運行。

        book為一個列表，元素個數為節點數，它的作用是，當已經確定某點到某點的最小距離時，進行標記，若有其他路徑包括這條路徑，即可減少程序的計算。

        dis為最終返回的路徑列表，表示從某點到某點的最小路徑，一共有n個。

        minpath存儲某點到某點的中會經過的節點。path中的節點由它決定。

import numpy as np
network = np.array([[0,2,4,0,0,0,0],
[2,0,0,3,3,1,0],
[4,0,0,2,3,1,0],
[0,3,2,0,0,0,1],
[0,3,3,0,0,0,3],
[0,1,1,0,0,0,4],
[0,0,0,1,3,4,0]])
def Dijkstra(network,s,d): # 迪傑斯特拉算法算s到t的最短路徑，並返回該路徑和距離
print("Start Dijstra Path……")
path = [] # 儲存s到d的最短路徑
n = len(network) # 節點個數
fmax = np.inf
w = [[0 for i in range(n)] for j in range(n)]
book = [0 for i in range(n)] # 是否已經是最小的標記列表
dis = [fmax for i in range(n)] # s到其他節點的最小距離
book[s-1] = 1 # 節點編號從1開始，列表序號從0開始
midpath = [-1 for i in range(n)] # 上一跳列表

         這一步就是將w矩陣初始化，變成程序能夠處理的標准矩陣，處理後的w中直連或者本身為fmax。對於i=s-1，其實是因為列表的序號是從0開始的，而我們習慣是從1開始

'''這個循環把原矩陣中的0標價為fmax，且認為直連就是最短（但事實並非如此）'''
for i in range(n):
for j in range(n):
if network[i][j] != 0:
w[i][j] = network[i][j] # 0→max
else:
w[i][j] = fmax
if i == s-1 and network[i][j] != 0: # 直連的節點最小距離就是network[i][j]
dis[j] = network[i][j]

        接下來就是算法的主體部分，n-1次循環就是除了s的節點外的其他節點，for循環中第一個min是會不斷更新的，直到找到最短距離，它的作用即在下方的if判斷中，檢查是不是距離是不是小於min，如果是的話，對min進行更新，否則用u進行記錄，標記出已經找出最小路徑的點。dis最初的元素全為fmax，通過迭代更新其中的元素，此時通過這個for循環得到的還不是最小的，要在經過下一個循環。不過，最終得到的都是最小路徑。例如dis輸出為[inf, 2, 4, 5, 5, 3, 6]，即表示從第一個點出發，依次到各個點的最小距離。

        下一個以v為元素遍歷的for循環中，這一步用於比較直連是否是最短，如果不是，則換其他的，同時對minpath列表進行更新。此時最短距離已經更新完畢，接下來是得到路徑。

        j=d-1的解釋和上面的i一樣，都是由於習慣不同。

 '''算法主體'''
for i in range(n-1): # n-1次遍歷，除了s節點
min = fmax # min的值是一直變化的
for j in range(n):
if book[j] == 0 and dis[j] < min: # 如果未遍歷且距離最小，反復比較得出最短距離
min = dis[j]
u = j
book[u] = 1 # 標記已到達的節點
# u處於一個循環體內，從2到7遍歷
for v in range(1,n): # u直連的節點遍歷一遍
'''關鍵步驟，用於比較與此節點直連的節點的長度'''
if dis[v] > dis[u] + w[u][v]:
dis[v] = dis[u] + w[u][v]
midpath[v] = u+1 # 上一跳更新
j = d-1 # j是序號
path.append(d) # 因為存儲的是上一跳，所以先加入目的節點d，最後倒置

        在此循環中，只是s到d的最短路徑，並不包括其他點之間。

        對於後面那個reverse方法，從上面path添加d就可以知道，需要轉置，要不然就是反的

 while midpath[j] != -1:
path.append(midpath[j])
j = midpath[j]-1
path.append(s)
path.reverse() # 倒置列表
print('path:',path)
print(dis)

        至此，算法也就完成了，接下來，調用這個函數就行，試驗用A到G的最短路，即1到7.

Dijkstra(network,1,7)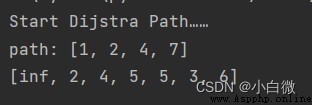

        結果表示，從A到G的最短距離為6，路徑為A—B—D—G。整個算法想要完整理解還是稍微有點困難（大佬避開嘿嘿），大家可以反復觀看以下，以下給出完整得代碼，便於觀察。

import numpy as np
def Dijkstra(network,s,d): # 迪傑斯特拉算法算s到t的最短路徑，並返回該路徑和代價
print("Start Dijstra Path……")
path = [] # 儲存s到t的最短路徑
n = len(network) # 節點個數
fmax = np.inf
w = [[0 for i in range(n)] for j in range(n)]
book = [0 for i in range(n)] # 是否已經是最小的標記列表
dis = [fmax for i in range(n)] # s到其他節點的最小距離
book[s-1] = 1 # 節點編號從1開始，列表序號從0開始
midpath = [-1 for i in range(n)] # 上一跳列表
# 此步可以省略，只要輸入矩陣規范就可
'''這個循環把原矩陣中的0標價為fmax，且認為直連就是最短（但事實並非如此）'''
for i in range(n):
for j in range(n):
if network[i][j] != 0:
w[i][j] = network[i][j] # 0→max
else:
w[i][j] = fmax
if i == s-1 and network[i][j] != 0: # 直連的節點最小距離就是network[i][j]
dis[j] = network[i][j]
# print('dis:',dis)
'''算法主體'''
for i in range(n-1): # n-1次遍歷，除了s節點
min = fmax # min的值是一直變化的
for j in range(n):
if book[j] == 0 and dis[j] < min: # 如果未遍歷且距離最小，反復比較得出最短距離
min = dis[j]
u = j
# print('book:',book)
book[u] = 1 # 標記已到達的節點
# print('u:',u)
# print('dis:',dis)
# u處於一個循環體內，從2到7遍歷
for v in range(1,n): # u直連的節點遍歷一遍
'''關鍵步驟，用於比較與此節點直連的節點的長度'''
if dis[v] > dis[u] + w[u][v]:
dis[v] = dis[u] + w[u][v]
midpath[v] = u+1 # 上一跳更新
j = d-1 # j是序號
path.append(d) # 因為存儲的是上一跳，所以先加入目的節點d，最後倒置
while midpath[j] != -1:
path.append(midpath[j])
j = midpath[j]-1
path.append(s)
path.reverse() # 倒置列表
print('path:',path)
print(midpath)
print(dis)
network = np.array([[0,2,4,0,0,0,0],
[2,0,0,3,3,1,0],
[4,0,0,2,3,1,0],
[0,3,2,0,0,0,1],
[0,3,3,0,0,0,3],
[0,1,1,0,0,0,4],
[0,0,0,1,3,4,0]])
Dijkstra(network,1,7)

 第三方庫解決方法

        如果大家實在看不懂上面的代碼，但又想用這個方法，這邊給出了第三方庫的解決方案，使用networkx庫，由於對這個庫了解不是很深，目前我只知道這個庫可以畫這類圖，以及用Dijkstra算法求最短路，最大流問題。接下來就用代碼，跟大家介紹以下這個方法

import networkx as nx
dis = [(0,1,2),(0,2,4),(1,3,3),(1,4,3),(1,5,1),(2,3,2),(2,4,3),(2,5,1),(3,6,1),
(4,6,3),(5,6,4)]
g = nx.Graph()
g.add_weighted_edges_from(dis)
a = nx.to_numpy_matrix(g,nodelist=range(7))
p = nx.dijkstra_path(g,source=0,target=6,weight='weight')
d = nx.dijkstra_path_length(g,0,6,weight='weight')
print('最短路徑為p={},最短距離為d={}'.format(p,d))

        同樣是用上面的例子，但是對比之下，代碼就少了很多。簡單介紹一下。

        第一個dis是一個列表，（0，1，2）表示從A到B的距離為2，，以此類推。

        g為初始化一個圖，Graph表示生成無向圖。

        接下來為圖添加節點和路權，參數為dis

        a對應生成的鄰接矩陣。

        p使用Dijkstra算法得到最短路徑，d得到最短距離。

         可以看出，和上面的代碼算法得到結果一致，不過要看那個p列表，可以全部元素＋1，即和上面的代碼運行結果一致。

案例——設備更新問題

        接下來用一道題實踐一下，雖然跟直接說某點到某點之間的最短路徑不同，但是本質是一樣的。不過這題我也只是試了一下，不一定保證對，所以大家可以思考一下，希望能對大家有所啟發。

        某企業在今後5年內需使用一台機器，該種機器的每年購置費和維修費（與機器的役齡有關）如下表所示。試制定機器購置和更新計劃，使5年內的成本最小。

年份

1

2

3

4

5

購置費

維修費

11

5

11

6

12

8

12

11

13

18

        我的想法是這樣的：

        令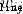表示第i年初買進用到第j-1年末中所包含的所有費用，此時wij即包含第i年買進時的購置費和j-i年的維修費用，故可知

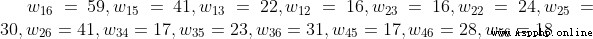
        用networkx庫畫出對應的圖，如下所示：

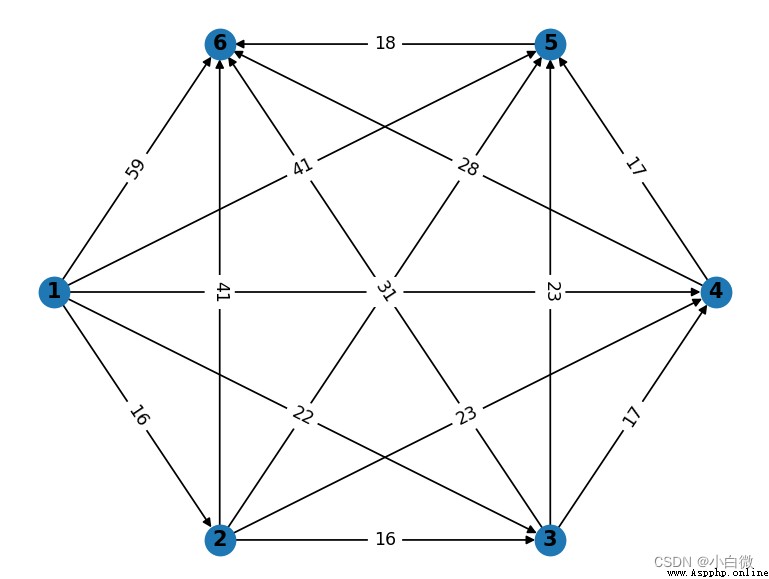
         最終用代碼解得，第一年買進用到第三年，然後在第三年買入用到第五年末，可使費用最低，為53單位。下面為代碼

import networkx as nx
import numpy as np
import pylab as plt
dis = [(1,5,41),(1,4,30),(1,3,22),(1,2,16),(1,6,59),(2,3,16),
(2,4,23),(2,5,30),(2,6,41),(3,4,17),(3,5,23),(3,6,31),
(4,5,17),(4,6,28),(5,6,18)]
g = nx.DiGraph()
g.add_nodes_from(range(1,7))
g.add_weighted_edges_from(dis)
pos = nx.shell_layout(g)
w = nx.get_edge_attributes(g,'weight')
nx.draw(g,pos,with_labels=True,font_weight='bold',font_size=12)
nx.draw_networkx_edge_labels(g,pos,edge_labels=w)
plt.show()
a = nx.to_numpy_matrix(g,nodelist=range(1,7))
p = nx.dijkstra_path(g,source=1,target=6,weight='weight')
d = nx.dijkstra_path_length(g,1,6,weight='weight')
print(p,d,sep='\n')

        g.add_nodes_from表示增加節點，g.add_weighted_edges_from表示增加路權，參數位dis，pos為作圖的一個參數，代碼從w開始到plt.show都是為作圖環節（如不需要，可以忽略）。接下來和上面示例一致，用Dijkstra算法解決。

總結

        使用算法一步一步算還是比較困難的，所謂算法就是給人想的，程序是代碼想的，關鍵就是如何讓電腦理解你的想法，不過這個Dijkstra算法有現成的庫還是比較方便的，當然也不要只是局限於求某點到某點的最短距離，可以引申一下，達到真正理解。

        算法，還是需要多練。對於上面的代碼和算法的解釋，如果有錯誤的地方，歡迎各位大神批評指正。有不懂的地方，也可以評論區或者直接私信我。

        創作不易，謝謝點贊——收藏——關注！！！