Python Detailed explanation Project Euler（ The Euler plan ）
The Euler plan It's a series of challenging math and computer programming problems ; The difficulty is comparable to that of Niuke , The buckle is more challenging . Not just math , It also needs the help of computer programming skills to solve , It is also a collection of topic tests to exercise the thinking of data analysts .
『Project Euler Mini tutorial 』 The necessary Euler plan for writing questions Python Edition summary post
Topic translation
In less than 10 Of the natural number , Yes 4 Yes 3 or 5 Multiple , Their sum is 23.
Similarly ,3 or 5 Less than 1000 , Find the sum of multiples .
Problem solving
A more direct solution would 1000 All of the following 3 or 5 The multiples of are listed and then summed .
def hoge(num):
ans = 0 # Define the cumulative sum base value
for n in range(1, num):
if n % 3 == 0 or n % 5 == 0: # The remainder operation is 0 That is, multiple
ans += n
return ans
print (hoge(1000))
>>> 233168
Topic translation
The numbers in Fibonacci series are all the sum of the first two terms , Suppose the first and second terms are 1 And 2, The first ten items are ：
1,2,3,5,8,13,21,34,55,89
Consider not more than four million Fibonacci Numbers , Calculate the sum of even Fibonacci numbers .
Problem solving
According to the rule of Fibonacci number , This sequence starts at number one 3 A start , Each of these terms is equal to the sum of the first two terms .
So we need to determine the first two items , A cumulative sum item performs basic data operations .
def hoge(num):
x = 1
y = 2
ans = 0
while y <= num:
if y % 2 == 0: # Even number judgment , Otherwise it adds up
ans = ans + y
y = x + y
x = y - x
return ans
print(hoge(4000000))
>>> 4613732
Topic translation
13195 What's the prime factor for 5、7、13、29.
seek 600851475143 The maximum prime factor of .
Problem solving
def hoge(num):
x = 2
soinsu = set() # Create an empty collection
# The result of the cycle is 1 Stop the cycle when you start
while 1:
# Number less than 2 It doesn't make any sense Returns an empty
if num < 2:
return None
# A number equal to itself is added to the set Stop the cycle
if num == x:
soinsu.add(x)
break
# Numbers can be added to a set and divided by an integer
elif num % x == 0:
soinsu.add(x)
num = num / x
else:
x += 1
return max(soinsu)
print (hoge(600851475143))
>>> 6857
Topic translation
Palindrome number is the same number read from front to back and from back to front . By two 2 The maximum number of palindromes obtained by multiplying digits is 9009 = 91 x 99.
Ask for two 3 The maximum number of palindromes obtained by multiplying digits .
Problem solving
def hoge(num):
min = 10 ** (num - 1) # The minimum value of the cycle calculation
max = 10 ** num -1 # The maximum value of the cycle calculation
ans = 0 # Base value
for x in range(min, max):
for y in range(min, max):
if str(x * y) == str(x * y)[::-1]: # Compare whether the reverse is equal in the form of string
if (x * y) > ans: # The assignment judgment seeks the maximum result and finally returns
ans = x * y
return ans
print (hoge(3))
>>> 906609
Topic translation
2520 Is the smallest that can be 1 To 10 The number divided by all integers of . So 1 To 20 What is the smallest positive number of all integers of ？
Problem solving
def hoge(num):
ans = num # Set a base multiple
while 1:
flg = True
for x in range(1, num+1):
if ans % x != 0:
flg = False
break
if flg == True:
break
else:
ans = ans + num # Accumulate in multiples until there is a result
return ans
print (hoge(20))
>>> 232792560
Topic translation
The sum of the squares of the first ten natural numbers is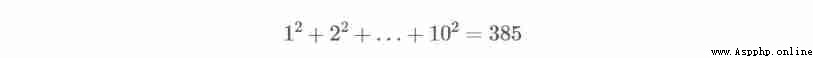 
The square of the sum of the first ten natural numbers is 
therefore , The difference between the sum of the squares of the first ten numbers and the sum of the squares is 3025-385=2640.
Find the difference between the sum of the squares of the first 100 numbers and the sum of the squares .
Problem solving
def hoge(num):
result = (
sum(range(1, num+1)) ** 2) - sum([ x ** 2 for x in range(1, num+1) ]
)
return result
print (hoge(100))
>>> 25164150
Topic translation
Former 6 Prime numbers are 2、3、5、7、11 and 13.
The first 10001 What is the prime number .
Problem solving
def hoge(num):
cnt = 0
x = 2
while 1:
flg = True
for y in range(2, x): # Can be divided by itself
if x % y == 0:
flg = False
break
if flg == True: # Count = num stop it
cnt += 1
if num == cnt:
break
x += 1
return x
print hoge(10001)
>>> 104743
Topic translation
As follows 1000 In figures , The maximum product of four consecutive numbers is 9 x 9 x 8 x 9 = 5832 .
73167176531330624919225119674426574742355349194934 96983520312774506326239578318016984801869478851843 85861560789112949495459501737958331952853208805511 12540698747158523863050715693290963295227443043557 66896648950445244523161731856403098711121722383113 62229893423380308135336276614282806444486645238749 30358907296290491560440772390713810515859307960866 70172427121883998797908792274921901699720888093776 65727333001053367881220235421809751254540594752243 52584907711670556013604839586446706324415722155397 53697817977846174064955149290862569321978468622482 83972241375657056057490261407972968652414535100474 82166370484403199890008895243450658541227588666881 16427171479924442928230863465674813919123162824586 17866458359124566529476545682848912883142607690042 24219022671055626321111109370544217506941658960408 07198403850962455444362981230987879927244284909188 84580156166097919133875499200524063689912560717606 05886116467109405077541002256983155200055935729725 71636269561882670428252483600823257530420752963450
Please this 1000 The maximum product of thirteen consecutive digits in the number of digits .
Problem solving
numbers = ''' 73167176531330624919225119674426574742355349194934 96983520312774506326239578318016984801869478851843 85861560789112949495459501737958331952853208805511 12540698747158523863050715693290963295227443043557 66896648950445244523161731856403098711121722383113 62229893423380308135336276614282806444486645238749 30358907296290491560440772390713810515859307960866 70172427121883998797908792274921901699720888093776 65727333001053367881220235421809751254540594752243 52584907711670556013604839586446706324415722155397 53697817977846174064955149290862569321978468622482 83972241375657056057490261407972968652414535100474 82166370484403199890008895243450658541227588666881 16427171479924442928230863465674813919123162824586 17866458359124566529476545682848912883142607690042 24219022671055626321111109370544217506941658960408 07198403850962455444362981230987879927244284909188 84580156166097919133875499200524063689912560717606 05886116467109405077541002256983155200055935729725 71636269561882670428252483600823257530420752963450 '''
def hoge(numbers, num):
numbers = numbers.replace(' ', '').replace('\n', '')
ans = 0
for i in range(len(numbers) - num + 1):
x = list(numbers[i:(i+num)])
x = [ int(y) for y in x ]
tmp_ans = 1
for z in x:
tmp_ans *= z
if ans < tmp_ans:
ans = tmp_ans
return ans
print (hoge(numbers, 13))
>>> 23514624000
Topic translation
Pythagorean triples consist of three natural numbers a < b < c form , And satisfy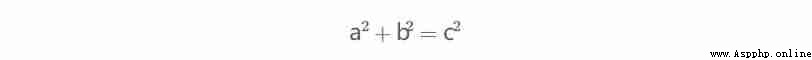 
for example
There is and only one Pythagorean triple satisfying a + b +c = 1000. Find the product of this triple abc.
Problem solving
def hoge(num):
for a in range(1, num):
for b in range(1, num):
if a + b > num - 1:
break
c2 = a ** 2 + b ** 2
for c in range(1, int(c2/2)):
if c ** 2 > c2:
break
elif c ** 2 == c2:
if a ** 2 + b ** 2 == c ** 2 and a + b + c == num:
return a * b * c
print(hoge(1000))
>>> 31875000
Topic translation
All less than 10 The sum of prime numbers of is 2 + 3 + 5 + 7 = 17.
Find the sum of all prime numbers less than two million .
Problem solving
def hoge(num):
sosu = []
for x in range(2, num + 1):
flg = True
for y in sosu:
if x % y == 0:
flg = False
break
if flg == True:
for y in range(max(sosu) + 1 if sosu else 2, int(x / 2 + 1)):
if x % y == 0:
flg = False
break
if flg == True:
sosu.append(x)
return sum(sosu)
print(hoge(2000000))
>>> 142913828922
[Natural language processing] Python based on logistic regression model for movie review sentiment analysis project combat
說明：這是一個機器學習實戰項目（附帶數據+代碼+文檔+視頻講
Python daily practice (Niuke new question bank) - day 11: Circular sentences
List of articles 1. Friends pr
