Python中的集合(set)是一個無序的不重復元素序列，如果在初始化時有重復的元素，重復的元素會被合並處理。
可以使用花括號 { } 或者 set() 函數創建集合，注意：創建一個空集合必須用 set() 而不是 { }，因為 { } 是用來創建一個空字典。
接下來，通過示例來學習Python中的集合(set)及其操作方法。
聲明：博主(昊虹圖像算法)寫這篇博文時，用的Python的版本號為3.9.10。
創建方法有兩種：
parame = {
value01,value02,...}
或
set(value)
示例代碼如下：
set1 = {
'pear', 'banana', 'orange', 'apple'}
set2 = {
'apple', 'orange', 'apple', 'pear', 'orange', 'banana'}
set3 = set('abracadabra')
set4 = set('abcdefg')
運行結果如下：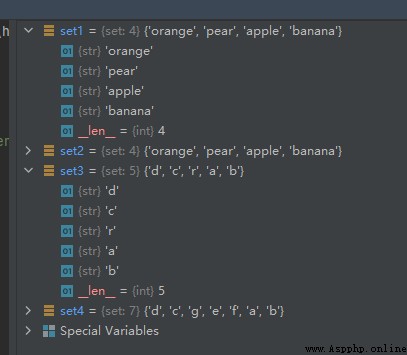
從上面的運行結果可以看出，set2和set3中的重復元素都被合並了。
對比列表的存儲結構：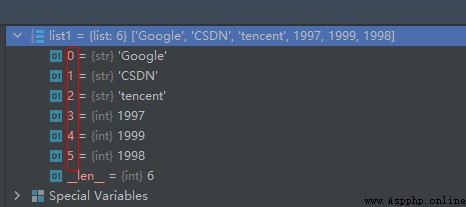
我們是不是可以作這樣一種推測：集合中的元素不分順序？答：是的，Python集合的特點之一就是無序性。
示例代碼如下：
set1 = {
'pear', 'banana', 'orange', 'apple'}
set1.add('kkk')
運行結果如下：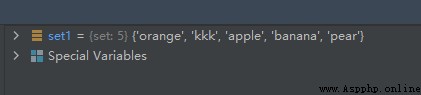
set1 = {
'pear', 'banana', 'orange', 'apple'}
set1.update({
'kkk', 'ppp'})
運行結果如下：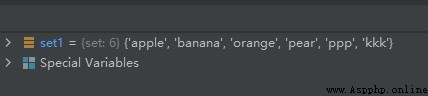
示例代碼如下：
set1 = {
'pear', 'banana', 'orange', 'apple'}
set1.remove('pear')
set2 = {
'pear', 'banana', 'orange', 'apple'}
set2.remove('orange')
運行結果如下：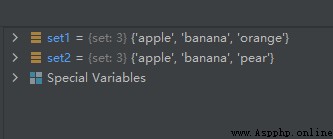
方法remove()和方法discard()的區別在於，方法remove()在移除元素時，如果元素不存在，會報錯，中止程序運行，而方法discard()不會。
示例代碼如下：
set1 = {
'pear', 'banana', 'orange', 'apple'}
set1.pop()
運行兩次，結果如下：
第一次：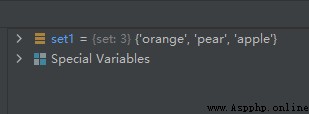
第二次：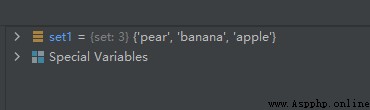
可見，第一次隨機刪除的是元素’banana’，第二次隨機刪除的是元素’orange’。
實際上， pop()方法會對集合進行無序的排列，然後將這個無序排列集合的左面第一個元素進行刪除。所以我們看到原集合中元素的相對位置都變了。
示例代碼如下：
set1 = {
'pear', 'banana', 'orange', 'apple'}
count1 = len(set1)
運行結果如下：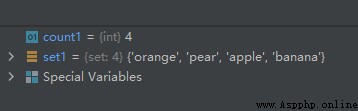
示例代碼如下：
set1 = {
'pear', 'banana', 'orange', 'apple'}
set2 = {
'pear', 'banana', 'orange', 'apple'}
set1.clear()
運行結果如下：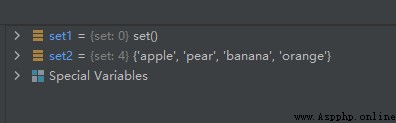
示例代碼如下：
set1 = {
'pear', 'banana', 'orange', 'apple'}
bool1 = 'apple' in set1
bool2 = 'swh' in set1
運行結果如下：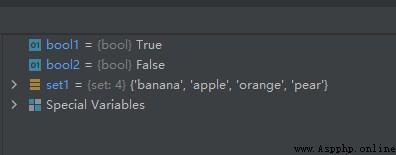
方法difference() 返回兩個集合的差集，差集是指這個集合的元素在集合x中，但不在集合y中。
設z表示集合x與y的差集，則z=x-(x∩y)。
示例代碼如下：
x = {
"apple", "banana", "cherry"}
y = {
"apple", "google", "microsoft"}
z1 = x.difference(y)
z2 = x-y
運行結果如下：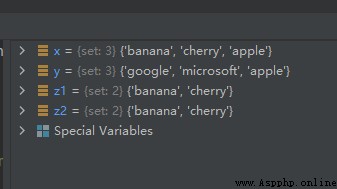
方法difference_update()實際上和方法difference()做的是同樣的運算，只是方法difference()做的是運算：z=x-(x∩y) 而方法difference_update()做的是運算：x=x-(x∩y)
示例代碼如下：
x = {
"apple", "banana", "cherry"}
y = {
"apple", "google", "microsoft"}
x.difference_update(y)
運行結果如下：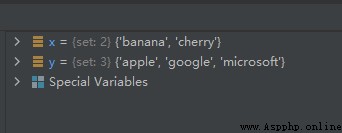
方法intersection()有返回值，而方法intersection_update()沒有返回值。
示例代碼如下：
x1 = {
"apple", "banana", "cherry"}
x2 = {
"apple", "banana", "cherry"}
y = {
"apple", "google", "microsoft"}
z1 = x1.intersection(y)
z2 = x1 & y
x2.intersection_update(y)
運行結果如下：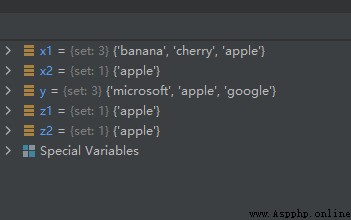
isdisjoint() 方法用於判斷兩個集合是否包含相同的元素，如果沒有返回 True，否則返回 False。。
示例代碼如下：
x = {
'apple', 'banana', 'cherry'}
y1 = {
'apple', 'google', 'microsoft'}
y2 = {
'facebook', 'google', 'microsoft'}
bool1 = x.isdisjoint(y1)
bool2 = x.isdisjoint(y2)
運行結果如下：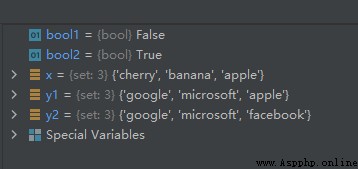
分析：y1中有x中的元素’apple’，所以bool1值為False; y2中沒有x中的元素，所以bool2值為True。
示例代碼如下：
x = {
"a", "b", "c"}
y1 = {
"f", "e", "d", "c", "b", "a"}
y2 = {
"f", "e", "d", "g", "h", "m"}
bool1 = x.issubset(y1)
bool2 = x.issubset(y2)
運行結果如下：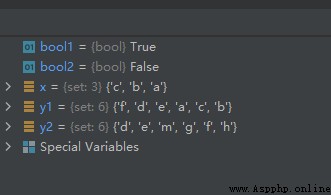
示例代碼如下：
x = {
'a', 'b', 'c', 'd', 'e', 'f'}
y1 = {
'a', 'b', 'c'}
y2 = {
'g', 'h', 'i'}
bool1 = x.issuperset(y1)
bool2 = x.issuperset(y2)
運行結果如下：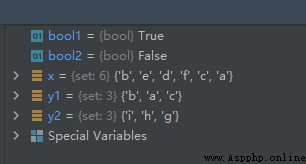
方法symmetric_difference()和運算符“^”是等價的，所以下面對方法symmetric_difference()的介紹就是對運算符“^”的介紹。
設兩個集合為x，y，z是方法symmetric_difference()的結果，則：
z=[x-(x∩y)]+[y-(x∩y)]
示例代碼如下：
x = {
1, 2, 3, 4, 5, 6}
y = {
1, 2, 3, 7, 8, 9}
z1 = x.symmetric_difference(y)
z2 = x ^ y
運行結果如下：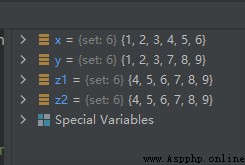
方法symmetric_difference_update()和symmetric_difference()做的運算是一樣的，惟一的區別是symmetric_difference_update()無返回值，symmetric_difference()有返回值：
symmetric_difference()的運算式如下：
z=[x-(x∩y)]+[y-(x∩y)]
而symmetric_difference_update()的運算式如下：
x = [x-(x∩y)]+[y-(x∩y)]
示例代碼如下：
x = {
1, 2, 3, 4, 5, 6}
y = {
1, 2, 3, 7, 8, 9}
x.symmetric_difference_update(y)
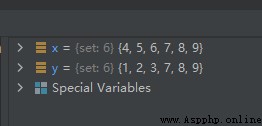
示例代碼如下：
x1 = {
1, 2}
x2 = {
3, 4}
x3 = {
5, 6}
x4 = {
7, 8}
y1 = set.union(x1, x2, x3)
y2 = set.union(x1, x2, x3, x4)
y3 = x1 | x2 | x3
y4 = x1 | x2 | x3 | x4
運行結果如下：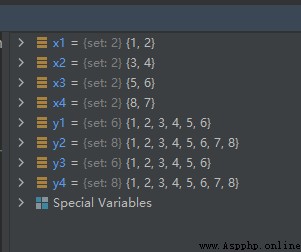
示例代碼如下：
fruits = {
"apple", "banana", "cherry"}
x = fruits.copy()
運行結果如下：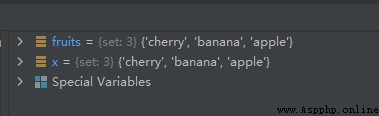
參考資料：
https://blog.csdn.net/wenhao_ir/article/details/125100220
Vue and Django front and back end separation practice (login function)
Vue and Django Front and back
解決python UnicodeEncodeError: ‘gbk‘ codec can‘t encode character ‘\xb5‘ in position 255: illegal mult
UnicodeEncodeError: gbk codec
