Python The set in (set) Is an unordered sequence of non-repeating elements , If there are duplicate elements during initialization , Duplicate elements are merged .
Curly braces can be used { } perhaps set() Function to create a collection , Be careful : To create an empty collection, you must use the set() instead of { }, because { } Is used to create an empty dictionary .
Next , Learn by example Python The set in (set) And its operation method .
Statement : Blogger ( Haohong image algorithm ) When writing this blog post , With Python Is the version number 3.9.10.
There are two ways to create :
parame = {
value01,value02,...}
or
set(value)
The sample code is as follows :
set1 = {
'pear', 'banana', 'orange', 'apple'}
set2 = {
'apple', 'orange', 'apple', 'pear', 'orange', 'banana'}
set3 = set('abracadabra')
set4 = set('abcdefg')
The operation results are as follows :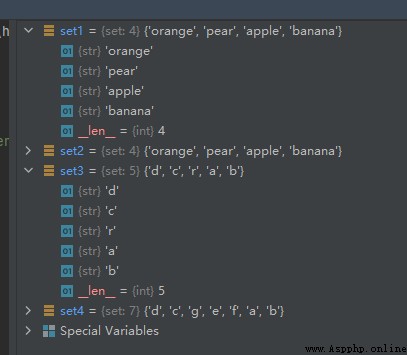
From the above running results, we can see that ,set2 and set3 The repeating elements in are merged .
Compare the storage structure of the list :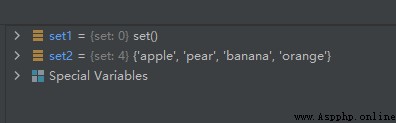
Can we make such a conjecture : The elements in the set are not in any order ? answer : Yes ,Python One of the characteristics of sets is disorder .
The sample code is as follows :
set1 = {
'pear', 'banana', 'orange', 'apple'}
set1.add('kkk')
The operation results are as follows :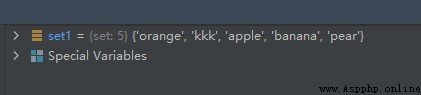
set1 = {
'pear', 'banana', 'orange', 'apple'}
set1.update({
'kkk', 'ppp'})
The operation results are as follows :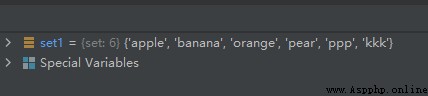
The sample code is as follows :
set1 = {
'pear', 'banana', 'orange', 'apple'}
set1.remove('pear')
set2 = {
'pear', 'banana', 'orange', 'apple'}
set2.remove('orange')
The operation results are as follows :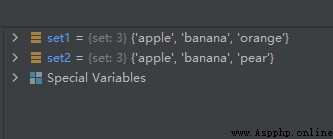
Method remove() And methods discard() The difference is that , Method remove() When removing elements , If the element does not exist , Will report a mistake , Abort program running , The method discard() Can't .
The sample code is as follows :
set1 = {
'pear', 'banana', 'orange', 'apple'}
set1.pop()
Run two times , give the result as follows :
for the first time :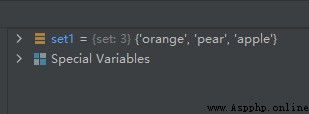
The second time :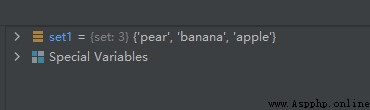
so , The first random deletion is the element ’banana’, The second random deletion is the element ’orange’.
actually , pop() Method will arrange the collection disorderly , Then delete the first element on the left of the unordered set . So we see that the relative positions of the elements in the original set have changed .
The sample code is as follows :
set1 = {
'pear', 'banana', 'orange', 'apple'}
count1 = len(set1)
The operation results are as follows :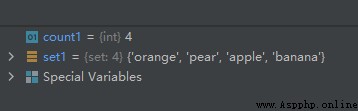
The sample code is as follows :
set1 = {
'pear', 'banana', 'orange', 'apple'}
set2 = {
'pear', 'banana', 'orange', 'apple'}
set1.clear()
The operation results are as follows :
The sample code is as follows :
set1 = {
'pear', 'banana', 'orange', 'apple'}
bool1 = 'apple' in set1
bool2 = 'swh' in set1
The operation results are as follows :
Method difference() Returns the difference set of two sets , A difference set is a set of elements in a set x in , But not in the assembly y in .
set up z Represents a collection x And y The difference between the set , be z=x-(x∩y).
The sample code is as follows :
x = {
"apple", "banana", "cherry"}
y = {
"apple", "google", "microsoft"}
z1 = x.difference(y)
z2 = x-y
The operation results are as follows :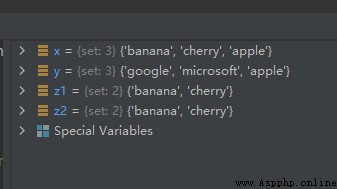
Method difference_update() In fact and method difference() Doing the same thing , Just the way difference() It's an operation :z=x-(x∩y) The method difference_update() It's an operation :x=x-(x∩y)
The sample code is as follows :
x = {
"apple", "banana", "cherry"}
y = {
"apple", "google", "microsoft"}
x.difference_update(y)
The operation results are as follows :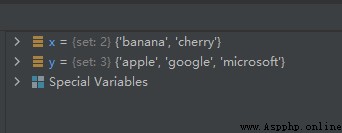
Method intersection() There is a return value , The method intersection_update() no return value .
The sample code is as follows :
x1 = {
"apple", "banana", "cherry"}
x2 = {
"apple", "banana", "cherry"}
y = {
"apple", "google", "microsoft"}
z1 = x1.intersection(y)
z2 = x1 & y
x2.intersection_update(y)
The operation results are as follows :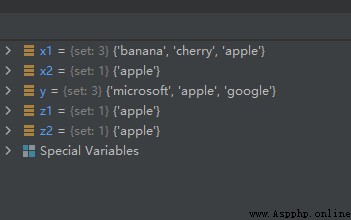
isdisjoint() Method is used to determine whether two sets contain the same element , If there is no return True, Otherwise return to False..
The sample code is as follows :
x = {
'apple', 'banana', 'cherry'}
y1 = {
'apple', 'google', 'microsoft'}
y2 = {
'facebook', 'google', 'microsoft'}
bool1 = x.isdisjoint(y1)
bool2 = x.isdisjoint(y2)
The operation results are as follows :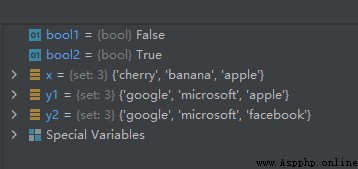
analysis :y1 There is x The elements in ’apple’, therefore bool1 The value is False; y2 There is no x The elements in , therefore bool2 The value is True.
The sample code is as follows :
x = {
"a", "b", "c"}
y1 = {
"f", "e", "d", "c", "b", "a"}
y2 = {
"f", "e", "d", "g", "h", "m"}
bool1 = x.issubset(y1)
bool2 = x.issubset(y2)
The operation results are as follows :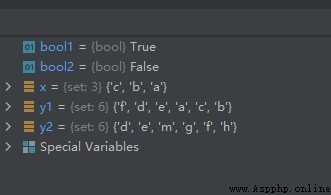
The sample code is as follows :
x = {
'a', 'b', 'c', 'd', 'e', 'f'}
y1 = {
'a', 'b', 'c'}
y2 = {
'g', 'h', 'i'}
bool1 = x.issuperset(y1)
bool2 = x.issuperset(y2)
The operation results are as follows :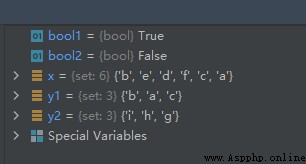
Method symmetric_difference() And operators “^” It is equivalent. , So here's the method symmetric_difference() The introduction of is to the operator “^” Introduction to .
Let two sets be x,y,z Is the method symmetric_difference() Result , be :
z=[x-(x∩y)]+[y-(x∩y)]
The sample code is as follows :
x = {
1, 2, 3, 4, 5, 6}
y = {
1, 2, 3, 7, 8, 9}
z1 = x.symmetric_difference(y)
z2 = x ^ y
The operation results are as follows :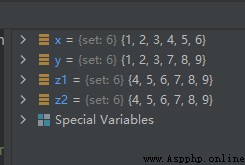
Method symmetric_difference_update() and symmetric_difference() The operations are the same , The only difference is symmetric_difference_update() No return value ,symmetric_difference() There is a return value :
symmetric_difference() The expression of is as follows :
z=[x-(x∩y)]+[y-(x∩y)]
and symmetric_difference_update() The expression of is as follows :
x = [x-(x∩y)]+[y-(x∩y)]
The sample code is as follows :
x = {
1, 2, 3, 4, 5, 6}
y = {
1, 2, 3, 7, 8, 9}
x.symmetric_difference_update(y)
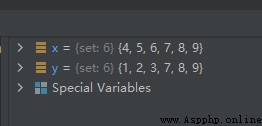
The sample code is as follows :
x1 = {
1, 2}
x2 = {
3, 4}
x3 = {
5, 6}
x4 = {
7, 8}
y1 = set.union(x1, x2, x3)
y2 = set.union(x1, x2, x3, x4)
y3 = x1 | x2 | x3
y4 = x1 | x2 | x3 | x4
The operation results are as follows :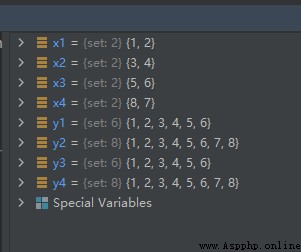
The sample code is as follows :
fruits = {
"apple", "banana", "cherry"}
x = fruits.copy()
The operation results are as follows :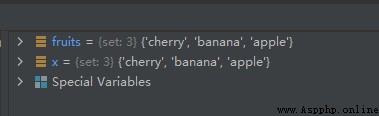
Reference material :
https://blog.csdn.net/wenhao_ir/article/details/125100220