
If you use Python Any coding done , Then you probably used numbers in a program . for example , You might use an integer to specify the index of a value in the list . however Python The numbers in are not just their original values . Let's take a look at what you may not know about Python Three things about numbers in .
Python There is a concept called : Everything is the object . You are in Python The first object learned in "HelloWorld" Is a representation of a string str object .
Then you learned that strings have methods , for example .lower() Method , It returns a new string of all lowercase characters :
>>> "HELLO". lower()
'hello'
For example, capital letters capitalize(), Returns a copy of the string , The first character is capitalized , The rest are in lowercase .
>>> mystring = "hello python"
>>> print( mystring. capitalize())
Hello python
Python The numbers in are also objects , It's like a string , It has its own way . for example , You can use .to_bytes() Method :
>>> n = 255
>>> n. to_bytes( length = 2, byteorder = "big")
b'\x00\xff'
among ,length Parameter specifies the number of bytes to use in the string ,byteorder Parameter determines the order of bytes . for example , take byteorder Set to “big” Will return a byte string , The most important byte comes first , And will be byteorder Set to "little" Then put the least important byte in the front .
>>> n. to_bytes( length = 2, byteorder = "little")
b'\xff\x00'
255 Yes can be expressed as 8 The largest integer of a bit integer , So you can go to .to_bytes() Set in length=1 No problem :
>>> n. to_bytes( length = 1, byteorder = "big")
b'\xff'
however , If in .to_bytes() Lieutenant general length=1 Set to 256, Will receive OverflowError error :
>>> n = 256
>>> n. to_bytes( length = 1, byteorder = "big")
Traceback ( most recent call last):
File "<stdin>", line 1, in < module >
OverflowError: int too big to convert
You can use .from_bytes() Class method converts a byte string to an integer :
>>> int. from_bytes( b'\x06\xc1', byteorder = "big")
1729
Class method It is called from the class name instead of the class instance , This is the one above int On the call .from_bytes() Reason for method .
Floating point numbers also have methods . Perhaps the most useful method for floating point numbers is .is_integer() , It is used to check whether floating-point numbers have no decimal part :
>>> n = 2.0
>>> n. is_integer()
True
>>> n = 3.14
>>> n. is_integer()
False
An interesting floating point method is .as_integer_ratio() Method , It returns a tuple , It contains the numerator and denominator of the fraction representing the floating-point value :
>>> n = 0.75
>>> n. as_integer_ratio()
( 3, 4)
however , because Floating point means error , This method may return some unexpected values :
>>> n = 0.1
>>> n. as_integer_ratio()
( 3602879701896397, 36028797018963968)
if necessary , You can call methods on numeric types by enclosing text in parentheses :
>>> ( 255). to_bytes( length = 1, byteorder = "big")
b'\xff'
>>> ( 3.14). is_integer()
False
If you don't enclose integer text in parentheses , When you call a method, you will see a SyntaxError —— Though strangely , You don't need parentheses with floating point text :
>>> 255. to_bytes( length = 1, byteorder = "big")
File "<stdin>", line 1
255. to_bytes( length = 1, byteorder = "big")
^
SyntaxError: invalid syntax
>>> 3.14. is_integer()
False
You can go to In the document find Python A complete list of available methods for numeric types :
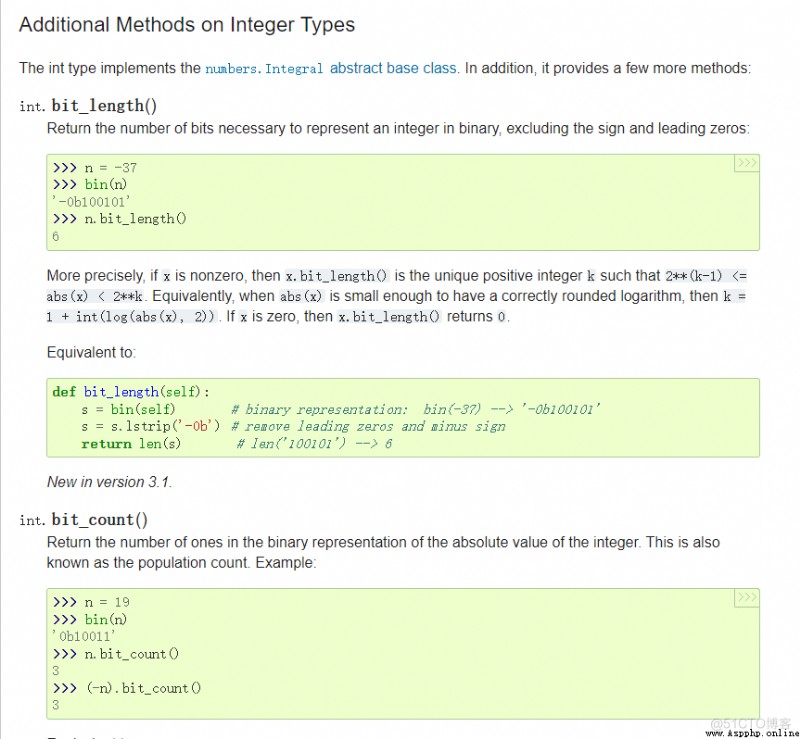
In mathematics , Numbers have a natural hierarchy . for example , All natural numbers are integers , All integers are rational , All rational numbers are real numbers , All real numbers are plural . Python The same is true of the numbers in . This “ The digital tower ” adopt numbers modular To express .
Python Every number in is Number An instance of a class :
>>> from numbers import Number
>>> # Integers inherit from Number
>>> isinstance( 1729, Number)
True
>>> # Floats inherit from Number
>>> isinstance( 3.14, Number)
True
>>> # Complex numbers inherit from Number
>>> isinstance( 1j, Number)
True
If you need to check Python Whether the value in is a number , But you don't care what kind of number the value is , Please use isinstance(value, Number).
Python Comes with four additional abstract types , The hierarchy starts with the most common number type , As shown below :
complex.float.Fraction.int and bool.You can verify all this in your terminal :
>>> import numbers
>>> # Complex numbers inherit from Complex
>>> isinstance( 1j, numbers. Complex)
True
>>> # Complex numbers are not Real
>>> isinstance( 1j, numbers. Real)
False
>>> # Floats are Real
>>> isinstance( 3.14, numbers. Real)
True
>>> # Floats are not Rational
>>> isinstance( 3.14, numbers. Rational)
False
>>> # Fractions are Rational
>>> from fractions import Fraction
>>> isinstance( Fraction( 1, 2), numbers. Rational)
True
>>> # Fractions are not Integral
>>> isinstance( Fraction( 1, 2), numbers. Integral)
False
>>> # Ints are Integral
>>> isinstance( 1729, numbers. Integral)
True
>>> # Bools are Integral
>>> isinstance( True, numbers. Integral)
True
>>> True == 1
True
>>> False == 0
True
however , Take a closer look at , A few things are right Python The number hierarchy of is a little weird .
Python There are four specific numerical types corresponding to the four abstract types in the digital tower :complex, float, Fraction, and int.
however Python There is a fifth number type , namely Decimal class , Used to accurately represent decimal numbers and overcome the limitations of floating-point operations .
As you might guess Decimal Number is a real number , But you are wrong :
>>> from decimal import Decimal
>>> import numbers
>>> isinstance( Decimal( "3.14159"), numbers. Real)
False
in fact ,Decimal The only type that a number inherits from is Python Of Number class :
>>> isinstance( Decimal( "3.14159"), numbers. Complex)
False
>>> isinstance( Decimal( "3.14159"), numbers. Rational)
False
>>> isinstance( Decimal( "3.14159"), numbers. Integral)
False
>>> isinstance( Decimal( "3.14159"), numbers. Number)
True
Decimal Do not inherit from Integral That makes sense . In a way ,Decimal Do not inherit from Rational It also makes sense . But why Decimal Not from Real or Complex Inheritance ?
The answer lies in CPython Source code in :
Decimal have Real abc All methods specified , But it should not be registered as Real, Because decimals do not interoperate with binary floating-point numbers ( for example :*Decimal('3.14') + 2.71828* Is not supported ). however , Abstract real numbers are expected to be interoperable ( namely , If R1 and R2 All are real numbers. , be *R1 + R2* Should be able to work ).
It all boils down to achieving .
On the other hand , Floating point numbers implement Real Abstract base class of , And used to represent real numbers . however , Due to limited memory constraints , Floating point numbers are only finite approximations of real numbers . It's confusing , As follows :
>>> 0.1 + 0.1 + 0.1 == 0.3
False
Floating point numbers are stored in memory as binary fractions , But this can cause some problems . It's like fractions 1/3 There is no finite decimal representation —— There are countless three after the decimal point . fraction 1/10 There is no finite binary fraction representation . let me put it another way , You can't just Precise precision will 0.1 Stored on the computer On —— Unless that computer has unlimited memory .
From a strictly mathematical point of view , All floating point numbers are rational numbers —— except float("inf") and float("nan"). But programmers use them to approximate real numbers and treat them as real numbers in most cases .
float("nan") Is a special floating point value , Express “ The digital ” value —— Commonly abbreviated as NaN value . But because of float It's the number type , therefore isinstance(float("nan"), Number) return True
you 're right :“ Not numbers ” Value is number .("not a number" values are numbers.)
This is the strange thing about floating point numbers .
Python The abstract number base type of allows you to create your own custom abstract and concrete number types . It is using Python About the types of numbers in , such as numbers The type of , You can define other numeric objects with special properties and methods .
for example , Consider the following classes ExtendedInteger, It has achieved a+b \sqrt p Numbers in form , among *a* ** and *b* Is an integer ,p** Prime number ( Please note that , Class does not enforce primes ):
import math
import numbers
class ExtendedInteger( numbers. Real):
def __init__( self, a, b, p = 2) - > None:
self. a = a
self. b = b
self. p = p
self. _val = a + ( b * math. sqrt( p))
def __repr__( self):
return f"{ self. __class__. __name__} ({ self. a} , { self. b} , { self. p} )"
def __str__( self):
return f"{ self. a} + { self. b} √{ self. p} "
def __trunc__( self):
return int( self. _val)
def __float__( self):
return float( self. _val)
def __hash__( self):
return hash( float( self. _val))
def __floor__( self):
return math. floor( self. _val)
def __ceil__( self):
return math. ceil( self. _val)
def __round__( self, ndigits = None):
return round( self. _val, ndigits = ndigits)
def __abs__( self):
return abs( self. _val)
def __floordiv__( self, other):
return self. _val / / other
def __rfloordiv__( self, other):
return other / / self. _val
def __truediv__( self, other):
return self. _val / other
def __rtruediv__( self, other):
return other / self. _val
def __mod__( self, other):
return self. _val % other
def __rmod__( self, other):
return other % self. _val
def __lt__( self, other):
return self. _val < other
def __le__( self, other):
return self. _val <= other
def __eq__( self, other):
return float( self) == float( other)
def __neg__( self):
return ExtendedInteger( - self. a, - self. b, self. p)
def __pos__( self):
return ExtendedInteger( + self. a, + self. b, self. p)
def __add__( self, other):
if isinstance( other, ExtendedInteger):
# If both instances have the same p value,
# return a new ExtendedInteger instance
if self. p == other. p:
new_a = self. a + other. a
new_b = self. b + other. b
return ExtendedInteger( new_a, new_b, self. p)
# Otherwise return a float
else:
return self. _val + other. _val
# If other is integral, add other to self's a value
elif isinstance( other, numbers. Integral):
new_a = self. a + other
return ExtendedInteger( new_a, self. b, self. p)
# If other is real, return a float
elif isinstance( other, numbers. Real):
return self. _val + other. _val
# If other is of unknown type, let other determine
# what to do
else:
return NotImplemented
def __radd__( self, other):
# Addition is commutative so defer to __add__
return self. __add__( other)
def __mul__( self, other):
if isinstance( other, ExtendedInteger):
# If both instances have the same p value,
# return a new ExtendedInteger instance
if self. p == other. p:
new_a = ( self. a * other. a) + ( self. b * other. b * self. p)
new_b = ( self. a * other. b) + ( self. b * other. a)
return ExtendedInteger( new_a, new_b, self. p)
# Otherwise, return a float
else:
return self. _val * other. _val
# If other is integral, multiply self's a and b by other
elif isinstance( other, numbers. Integral):
new_a = self. a * other
new_b = self. b * other
return ExtendedInteger( new_a, new_b, self. p)
# If other is real, return a float
elif isinstance( other, numbers. Real):
return self. _val * other
# If other is of unknown type, let other determine
# what to do
else:
return NotImplemented
def __rmul__( self, other):
# Multiplication is commutative so defer to __mul__
return self. __mul__( other)
def __pow__( self, exponent):
return self. _val < strong > exponent
def __rpow__( self, base):
return base < / strong > self. _val
You need to implement many dunder Method to ensure that the concrete type implements Real Interface . You must also consider .__add__() and .__mul__() And other methods Real Type interaction .
Realization ExtendedInteger after , You can now do the following :
>>> a = ExtendedInteger( 1, 2)
>>> b = ExtendedInteger( 2, 3)
>>> a
ExtendedInteger( 1, 2, 2)
>>> # Check that a is a Number
>>> isinstance( a, numbers. Number)
True
>>> # Check that a is Real
>>> isinstance( a, numbers. Real)
True
>>> print( a)
1 + 2 √2
>>> a * b
ExtendedInteger( 14, 7, 2)
>>> print( a * b)
14 + 7 √2
>>> float( a)
3.8284271247461903
Python Our digital hierarchy is very flexible . however , Of course , When implementing a type that derives from a built-in abstract base type , You should always be very careful . You need to make sure they get along well with others . Before implementing custom numeric types , You should read the documentation for the type implementer There are a few tips . Read... Carefully Fraction Of Realization It's also helpful .
So you have read the article . About Python Number in , Three things you may not know ( There may be more ):
Decimal and float A bit of abuse .I hope you learned something new ! Reference link :
 Computer graduation design Python+djangs freshman enrollment management system (source code + system + mysql database + Lw document)
Computer graduation design Python+djangs freshman enrollment management system (source code + system + mysql database + Lw document)
項目介紹每年都有大量的新生需要報到,但是很多時候因為是第一次
 [Python example] list comprehensive application - random allocation office
[Python example] list comprehensive application - random allocation office
demand : There are three offic