Not much work has been done today , The main reason is that I went to play ECS later , That thing has been configured for half a day , Huawei's , The school spent a lot of money to get it 320G Run a memory , The result is because centos7, still arch Of I even anaconda There is no official version of , Finally, I can only go to GitHub Make a suitable arch Of ,Python The version only goes to 3.7.1, Then my code is based on the new grammar , There are types , And does not support .
So today, we only did the work based on Kmeans++ To separate species groups , Originally, I wanted to do topology , however , The quality of those Chinese papers is really inferior , I didn't make it clear , I know the topology , But what strategy is used to obtain the adjacent points , After watching for a long time, there was nothing , If it's based on distance , You don't have to do it at high latitudes . At present, it is possible to follow the particle's ID To the . If so , I feel like I might as well just let it go .
It's a solemn reminder : The copyright of this article belongs to me , No one is allowed to copy , Carry , Use with my consent !
date :2022.6.21 DAY 2
There was a coding problem yesterday , Never found out , I ran for several times today and found that the result was not right , So I took what my former classmates had written PSO Compared with , At first I thought it was np The problem of , Maybe there is something wrong with deep and shallow replication , If you look closely, you can see that , For deep and shallow copy, I use deep copy ( By generating new list Realization ), Then I thought it was np The problem of , then , I wrote it in my code format ( Because it needs to be distributed , So you don't have to use a matrix ) Later, I found out that I forgot to update the velocity to the particle .
#coding=utf-8
# This is the most basic PSO Algorithm implementation , Used to test the rationality of the current algorithm architecture
# In addition, this gadget is also a tool class for optimization , The whole algorithm is to find the minimum value
import sys
import os
sys.path.append(os.path.abspath(os.path.dirname(os.getcwd())))
from ONEPSO.Bird import Bird
from ONEPSO.Config import *
from ONEPSO.Target import Target
import random
import time
class BasePso(object):
Population = None
Random = random.random
target = Target()
W = W
def __init__(self):
# For convenience , Let's start with 1 Start
self.Population = [Bird(ID) for ID in range(1,PopulationSize+1)]
def ComputeV(self,bird):
# This method is used to calculate the velocity drop
NewV=[]
for i in range(DIM):
v = bird.V[i]*self.W + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\
+C2*self.Random()*(bird.GBestX[i]-bird.X[i])
# Here, pay attention to judge whether it is beyond the scope
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def ComputeX(self,bird:Bird):
NewX = []
NewV = self.ComputeV(bird)
bird.V = NewV
for i in range(DIM):
x = bird.X[i]+NewV[i]
if(x>X_up):
x = X_up
elif(x<X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
# Initial population
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
# After the convenience, we get the globally optimal population
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
def Running(self):
# Here we begin to iterate
for iterate in range(1,IterationsNumber+1):
w = LinearW(iterate)
# This is a good one GBestX In fact, it is always the best thing in the next round
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
# Change to linear weight
self.W = w
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
# Here we still need to be more detailed unconditionally , Otherwise, here C1 Is failure
# if(y<=bird.Y):
# bird.X = x
# bird.Y = y
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
# The best in an individual must contain the best that the whole world has experienced
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
if __name__ == '__main__':
start = time.time()
basePso = BasePso()
basePso.InitPopulation()
basePso.Running()
end = time.time()
# for bird in basePso.Population:
# print(bird)
print(basePso.Population[0])
print(" It takes a long time :",end-start)
This part of the revision was made by referring to the original documents .
First of all Kmeans++ The implementation of the .
#coding=utf-8
# Because the selection of the center point is important for PSO It is important for many groups
# So here we choose Kmeans++ To choose the center point carefully
# The distance formula adopts European distance
import sys
import os
sys.path.append(os.path.abspath(os.path.dirname(os.getcwd())))
from ONEPSO.Bird import Bird
from ONEPSO.Config import *
import random
import math
class KmeansAdd(object):
choice = random.sample
ClusterCenters = []
def Divide(self,Popluations,Centers):
# Divide , Here, if the conditions are not met, it will be divided according to the last ethnic group
# Pay attention to the original CID It doesn't matter what the number is , As long as the classification is accurate, there is no problem
for bird in Popluations:
BirdCID = -1
Flag = float("inf")
for center in Centers:
dist = self.EuclideanDistan(bird,center)
if(dist<=Flag):
Flag=dist
BirdCID+=1
bird.CID=BirdCID
bird.DIST=Flag
def EuclideanDistan(self,bird,center):
# Euclidean distance formula
x1 = bird.X
x2 = center
dist = 0
for index in range(len(x1)):
dist+=math.pow((x1[index]-x2[index]),2)
return dist
def InitChoiceCenter(self,Population):
# Initialize pick Center , Choose one first , Then help me complete the initialization classification , At this time ClusterCenters What's stored is
# The center point we initialize
K = 1
self.ClusterCenters = self.choice(Population,K)
RelCenters = []
for i in range(K):
# Distribute CID
self.ClusterCenters[i].CID=(i)
RelCenters.append(self.ClusterCenters[i].X)
# This central point stores the coordinates of the points in the feasible region
self.ClusterCenters=RelCenters
# This completes the first partition
self.Divide(Population,self.ClusterCenters)
# Construct a weight model
Tim = ClusterNumber-K
for i in range(Tim):
K+=1
Weights = [bird.DIST for bird in Population]
Total = sum(Weights)
Weights=[weight/Total for weight in Weights]
# In using the roulette algorithm
x = -1
i = 0
Due = random.random()
while(i<Due):
x+=1
i+=Weights[x]
self.ClusterCenters.append(Population[x].X)
# Divide the center point again , Then by adding the center point , We can complete the division of sub populations
self.Divide(Population, self.ClusterCenters)
def RunningChoiceCenter(self,Population):
# Select the center point at runtime , Returns the calculated new center point
NewClusterCenterPoints={
}
Counter = {
}
# First initialize the counter , New central point
for CID in range(ClusterNumber):
Counter[CID]=0
for bird in Population:
if(not NewClusterCenterPoints.get(bird.CID)):
NewClusterCenterPoints[bird.CID]=bird.X
else:
NewClusterCenterPoints[bird.CID] = self.__ADD_X(NewClusterCenterPoints.get(bird.CID),bird.X)
Counter[bird.CID]=Counter[bird.CID] + 1
# Calculate the new center point
for CID in NewClusterCenterPoints.keys():
NewClusterCenterPoints[CID] = self.__Division_X(NewClusterCenterPoints.get(CID),Counter.get(CID))
return list(NewClusterCenterPoints.values())
def RunningDivide(self,Poplution,Iterate=0):
self.InitChoiceCenter(Poplution)
for epoch in range(K_Iterate):
NewClusterCenters = self.RunningChoiceCenter(Poplution)
if(
len(self.ClusterCenters)!=ClusterNumber or self.__SAME_Pred(self.ClusterCenters,NewClusterCenters)>=SAEMPRED
):
# print("Bad",epoch,Iterate,len(self.ClusterCenters))
break
else:
self.Divide(Poplution,NewClusterCenters)
self.ClusterCenters=NewClusterCenters
def __SAME_Pred(self,LastCenters,NewCenters):
# This gadget is used to calculate the similarity , If the similarity is found to exceed the threshold , So stop iterating
res = 0.
count=0
if(len(LastCenters)!=len(NewCenters)):
return False
for i in range(len(LastCenters)):
for j in range(len(LastCenters[i])):
res+=math.pow((LastCenters[i][j]-NewCenters[i][j]),2)
count+=1
res = 1-(res/count)
return res
def __ADD_X(self,X1,X2):
res = []
for i in range(len(X1)):
res.append(X1[i]+X2[i])
return res
def __Division_X(self,X1,X2):
res =[]
for i in range(len(X1)):
res.append(X1[i]/X2)
return res
This is still relatively simple , Mainly pay attention to initialization and general Kmeans Dissimilarity . Then we use the Euclidean distance here , Which distance formula is better , This is to be tested , I think it will be better , because , This PSO It is based on space .
Then the integration code is as follows :
#coding=utf-8
# Now it's based on Kmeans++ Write the dynamic division of sub populations PSO Algorithm .
import sys
import os
sys.path.append(os.path.abspath(os.path.dirname(os.getcwd())))
from ONEPSO.BasePso import BasePso
from ONEPSO.Config import *
from ONEPSO.Bird import Bird
import time
from ONEPSO.KmeansAdd import KmeansAdd
class DKMPSO(BasePso):
kmeansAdd = KmeansAdd()
def __init__(self):
super(DKMPSO,self).__init__()
self.kmeansAdd.RunningDivide(self.Population)
def ComputeV(self,bird):
# This method is used to calculate the velocity drop
NewV=[]
for i in range(DIM):
v = bird.V[i]*self.W + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\
+C2*self.Random()*(bird.GBestX[i]-bird.X[i]) + C3*self.Random()*(bird.CBestX[i]-bird.X[i])
# Here, pay attention to judge whether it is beyond the scope
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def ComputeX(self,bird):
NewX = []
NewV = self.ComputeV(bird)
bird.V = NewV
for i in range(DIM):
x = bird.X[i]+NewV[i]
if (x > X_up):
x = X_up
elif (x < X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
# Initial population
# This is to record the global optimal solution
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
# There is also a record Cluster Optimal solution
CBest = {
}
CFlag = {
}
for i in range(ClusterNumber):
CFlag[i]=float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
bird.CBestX = bird.X
bird.CBestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
if(bird.Y<=CFlag.get(bird.CID)):
CBest[bird.CID]=bird.X
CFlag[bird.CID] = bird.Y
# After the convenience, we get the globally optimal population
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
bird.CBestY=CFlag.get(bird.CID)
bird.CBestX=CBest.get(bird.CID)
def Running(self):
# Here we begin to iterate
for iterate in range(1,IterationsNumber+1):
w = LinearW(iterate)
# This is a good one GBestX In fact, it is always the best thing in the next round
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
CBest = {
}
CFlag = {
}
for i in range(ClusterNumber):
CFlag[i] = float("inf")
for bird in self.Population:
# Change to linear weight
self.W = w
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
# Here we still need to be more detailed unconditionally , Otherwise, here C1 Is failure
# if(y<=bird.Y):
# bird.X = x
# bird.PBestX = x
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
# The best in an individual must contain the best that the whole world has experienced
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
if (bird.Y <= CFlag.get(bird.CID)):
CBest[bird.CID] = bird.X
CFlag[bird.CID] = bird.Y
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
bird.CBestY = CFlag.get(bird.CID)
bird.CBestX = CBest.get(bird.CID)
if((iterate+1)%100==0):
self.kmeansAdd.RunningDivide(self.Population,iterate)
if __name__ == '__main__':
start = time.time()
dkmpso = DKMPSO()
dkmpso.InitPopulation()
dkmpso.Running()
end = time.time()
# for bird in dkmpso.Population:
# print(bird)
print(dkmpso.Population[0])
print(" It takes a long time :",end-start)
In fact, it is not much different from the original direct score , Just change a standard of division , Then here is every 100 The iteration is divided again , In fact, I feel that at the beginning , It will be better if you don't have to divide it after it is divided , This is also a better test .
First , We play multiple groups for the purpose of , First, prevent premature , Second, ensure uniformity ( Multiple targets on the back , If the particles all run in one direction , It's hard to get ahead ), Third Use more information , For the high latitude optimization problem .
I'm here for 10 Dimensions , And then probably right 100,200,1000,2000,10000… Experiments were done in the second iteration ( Probably 20 Multiple parameters , Then each group is about 10-20 Experiments ).
Then set each round K Second recalculation Center .
First , On the whole , No partition after initialization , The effect is the worst .
Then it is about how many rounds are tested , Probably the current setting method is , Divide by the number of iterations 5 It is better to , It's also faster . That is about five times 
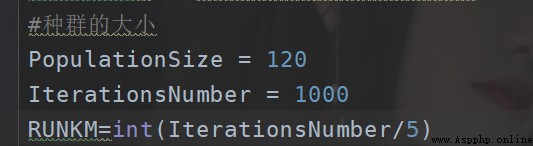
Using the most traditional particle swarm optimization is the best
The effect of using my direct molecular population is good
Using this has KMeans There is little difference between the effect of and without , There is not much difference , In general, I recommend those that do not exist . But for now Kmeans In fact, it is not used well , Because the update speed is different from that of the paper .
Of course, these are all in a limited number of experiments , Preliminary results , Each test does not run a 100+ To tell the truth, I don't believe this data . The chance is too high .
Then tomorrow we will study this topology and reinforcement learning , That topology paper is really ambiguous , There is also the article that introduces the use of topology , It's also , Not to look down upon Chinese papers , It is true that there is too much water . And the academic falsification of this paper is too easy to do , Because the same code , The results are different , A little beautification , Here comes the data .
But here , I'm still doing tests , Tell the truth , Keep revising .