當前還是正對單目標算法的優化,目的是為了能夠避免由於單目標算法本身的局限性導致多目標的效果驟降。
本次代碼采用Python實現,後期將轉移至Flink 平台。
鄭重提示:本文版權歸本人所有,任何人不得抄襲,搬運,使用需征得本人同意!
[1]廖延娜,李夢君,張婧琪.K均值聚類-粒子群優化多目標定位算法[J].電子設計工程,2018,26(02):56-60.
摘要:針對復雜圖像背景下的多目標定位問題,采用K均值聚類-粒子群優化聯合算法,應用排擠機制確定初始聚類質心;根據特征向量將目標粒子種群分為若干個子群,在每個目標子群中進行粒子優化更新;重復進行聚類和子群優化,直到各個目標子群得到最優解。將該算法運用到多車牌定位中,在實際采集大量停車場圖片的基礎上,設計了車牌目標粒子模型,特征向量和適應度函數,進行了算法的Matlab仿真。實驗結果表明:K均值聚類-粒子群優化實現了多個目標的准確自動定位,算法穩定收斂。
[2]郭成,張萬達,王波,王加富.多種群並行協作的粒子群算法[J].計算機與現代化,2022,(01):33-40.
摘要:針對高維復雜優化問題在求解時容易產生維數災難導致算法極易陷入局部最優的問題,提出一種能夠綜合考慮高維復雜優化問題的特性,動態調整進化策略的多種群並行協作的粒子群算法。該算法在分析高維復雜問題求解過程中的粒子特點的基礎上,建立融合環形拓撲、全連接形拓撲和馮諾依曼拓撲結構的粒子群算法的多種群並行協作的網絡模型。該模型結合3種拓撲結構的粒子群算法在解決高維復雜優化問題時的優點,設計一種基於多群落粒子廣播-反饋的動態進化策略及其進化算法,實現高維復雜優化環境中拓撲的動態適應,使算法在求解高維單峰函數和多峰函數時均具有較強的搜索能力。仿真結果表明,該算法在求解高維復雜優化問題的尋優精度和收斂速度方面均有良好的性能。
[3]羅德相,周永權,黃華娟,韋杏瓊.多種群粒子群優化算法[J].計算機工程與應用,2010,46(19):51-54.
摘要:將一定規模的粒子群平分成三個子群,並分別按基本粒子優化算法、ω自線性調整策略的粒子群算法和雲自適應粒子群算法三種不同規則進化,既保持各個子群和算法的獨立性和優越性,又不增加算法的復雜性,並提出"超社會"部分,重新定義了速度更換式子,同時還引入了擴張變異方法和擾動操作。實驗仿真結果表明,給出算法的全局搜索能力、收斂速度,精度和穩定性均有了顯著提高。
[4]楊道平.粒子群算法鄰域拓撲結構研究[J].中國高新技術企業,2009,(16):36-37.
摘要:粒子群算法(PSO算法)是一種啟發式全局優化技術。PSO的鄰域拓撲結構是決定粒子群優化算法效果的一個很重要的因素,不同鄰域拓撲結構的粒子群算法,效果差別很大。文章分析了鄰域拓撲結構與PSO算法的關系,闡述了粒子群算法鄰域拓撲結構研究現狀,提出了未來可能的研究方向。
這裡我參考了四篇論文,於是我這裡提出了三個優化想法,這裡先實現兩個版本.
日期:2022.6.20 DAY 1
先基於非矩陣運算實現最基本的PSO算法
基於第三個引用實現最簡單的算法。這個其實在PSO實現了,但是這個後面我想上強化學習優化,所以還得單獨搞成python的。
ok ,先來看到今天的第一個工作點,傳統的最基礎的在1995年提出的算法。
整個項目結構如下:
算法的基礎核心公式如下: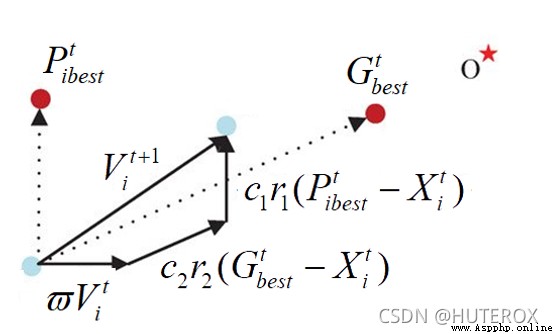
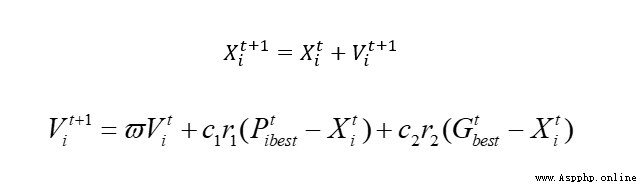
首先是配置
這個主要負責後面的各種配置,然後我們這邊統一是使用線性權重來做的。
# 相關參數的設置通過配置中心完成
C1=2.0
C2=2.0
C3=2.0
W = 0.4
#單目標下定義的維度
DIM = 2
X_down = -2.0
X_up = 2.0
V_min = -4.0
V_max = 4.0
#這個參數是後面優化多種群PSO算法的參數
ClusterSize = 20
ClusterNumber = 3
#種群的大小
PopulationSize = 60
IterationsNumber = 1000
def LinearW(iterate):
#傳入迭代次數
Wmax = 0.9
Wmin = 0.4
w = Wmax-(iterate*((Wmax-Wmin)/IterationsNumber))
return w
之後是我們的目標優化函數,這裡的話我也是單獨提取出來了,因為我打算先好好優化單目標,然後去優化多目標,之後咱們再找幾個實際的點去突破,然後文章就搞出來了,雖然也是有類似PlatEMO 這種平台,但是作為軟工本工的大二學子,我還是喜歡自己寫輪子,而且我後面還要上Flink,上流處理引擎走分布式(所以後面的代碼我不用矩陣,用類,用對象來表示更多的信息,單機無並發,多機可並發,如果是矩陣的話,別想了,很麻煩。
#這個玩意是用來定義需要優化的函數的地方
class Target(object):
def SquareSum(self,X:list):
res = 0
for x in X:
res+=x*x
return res
這個Bird就是我為了減少矩陣運算做的事情
雖然實際上我用numpy會很爽,直接矩陣並行運算,然後更新就行了,但是一單上了流處理,就難搞了,到後面如果搞的話,搞不好還是在一台機子上完成了矩陣運算,如果看Flink處理數據同步的機制的話,矩陣是不好拆分的,然後他是按照最慢的那個來的,如果拆分了,拆多少,怎麼合並,延時怎麼處理都是問題。
#這裡我們使用定義Class的方式實現PSO,便於後面調整
from ONEPSO.Config import *
import random
class Bird(object):
ID = 0
#這個是劃分多種群時的種群ID
CID = 0
Iterate = 0
Y = None
X = None
#記錄個體的最優值,這個關系到後面求取全局最優值
PbestY = None
PBestX = None
GBestX = None
GBestY = None
CBestY=None
CBestX=None
V = None
def __init__(self,ID):
self.ID = ID
self.V = [random.random() *(V_max-V_min) + V_min for _ in range(DIM)]
self.X = [random.random() *(X_up-X_down) + X_down for _ in range(DIM)]
def __str__(self):
return "ID:"+str(self.ID)+" -Fintess:%.2e:"%(self.Y)+" -X"+str(self.X)+" -PBestFitness:%.2e"%(self.PbestY)+" -PBestX:"+str(self.PBestX)+\
"\n -GBestFitness:%.2e"%(self.GBestY)+" -GBestX:"+str(self.GBestX)
之後是最基本的實現了
#這個是最基礎的PSO算法實現,用於測試當前算法架構的合理性
#此外這個玩意還是用來優化的工具類,整個算法是為了求取最小值
from ONEPSO.Bird import Bird
from ONEPSO.Config import *
from ONEPSO.Target import Target
import random
import time
class BasePso(object):
Population = None
Random = random.random
target = Target()
W = W
def __init__(self):
#為了方便,我們這邊直接先從1開始
self.Population = [Bird(ID) for ID in range(1,PopulationSize+1)]
def ComputeV(self,bird:Bird):
#這個方法是用來計算速度滴
NewV=[]
for i in range(DIM):
v = bird.V[i]*self.W + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\
+C2*self.Random()*(bird.GBestX[i]-bird.X[i])
#這裡注意判斷是否超出了范圍
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def ComputeX(self,bird:Bird):
NewX = []
NewV = self.ComputeV(bird)
for i in range(DIM):
x = bird.X[i]+NewV[i]
if(x>X_up):
x = X_up
elif(x<X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
#初始化種群
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
#便利了一遍我們得到了全局最優的種群
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
def Running(self):
#這裡開始進入迭代運算
for iterate in range(1,IterationsNumber+1):
w = LinearW(iterate)
#這個算的GBestX其實始終是在算下一輪的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
#更改為線性權重
self.W = w
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
# 這裡還是要無條件更細的,不然這裡的話C1就失效了
# if(y<=bird.Y):
# bird.X = x
# bird.PBestX = x
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
#個體中的最優一定包含了全局經歷過的最優值
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
if __name__ == '__main__':
start = time.time()
basePso = BasePso()
basePso.InitPopulation()
basePso.Running()
end = time.time()
for bird in basePso.Population:
print(bird)
print("花費時長:",end-start)
整個算法寫起來是很簡單的,而且用這種寫法也是最容易理解,最容易修改的,因為很多東西我就可以直接改了。
之後是我們多種群的。
這個我這裡先實現的是最簡單的這個,多種群的(其實寫這個也就是為了做測試,後面還有三個點要實現),還有幾篇文獻明天要處理一下。
文章這個東西,看懂了寫起代碼是真的快。
突然發現在學校實驗室混是真爽,不然現在還在CURD,還在八股文捏。
那麼這個代碼是這樣的,分三個小群,現在是直接分,三個組,然後更新方程變成這樣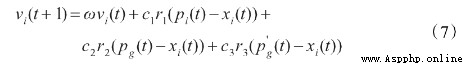
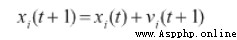
後面的兩個點,一個是圍繞這個分種群怎麼分,一個是圍繞這個種群之間如何交互,第一篇就提到了不同拓撲網絡的問題。最後一個是如何對參數進行優化,因為這個PSO,你也會發現這個參數對PSO的影響很大,例如C1,2,3的設置,這個意味著你後面會偏向哪一個,這裡我考慮用強化學習優化,先來個簡單的QL試試水。
#這個算法是打算在BasePso的基礎上,做一個簡單的多種群優化
from ONEPSO.BasePso import BasePso
from ONEPSO.Config import *
from ONEPSO.Bird import Bird
import time
class MPSOSimple(BasePso):
def __init__(self):
super(MPSOSimple,self).__init__()
self.Divide()
def Divide(self):
#先來一個最簡單的方法,硬分類
CID = 0
for bird in self.Population:
bird.CID=CID
if(bird.ID % ClusterSize==0):
if(CID<=ClusterNumber):
CID+=1
def ComputeV(self,bird:Bird):
#這個方法是用來計算速度滴
NewV=[]
for i in range(DIM):
v = bird.V[i]*self.W + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\
+C2*self.Random()*(bird.GBestX[i]-bird.X[i]) + C3*self.Random()*(bird.CBestX[i]-bird.X[i])
#這裡注意判斷是否超出了范圍
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def ComputeX(self,bird:Bird):
NewX = []
NewV = self.ComputeV(bird)
for i in range(DIM):
x = bird.X[i]+NewV[i]
if (x > X_up):
x = X_up
elif (x < X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
#初始化種群
#這個是記錄全局最優解的
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
#還有一個是記錄Cluster最優解的
CBest = {
}
CFlag = {
}
for i in range(ClusterNumber):
CFlag[i]=float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
bird.CBestX = bird.X
bird.CBestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
if(bird.Y<=CFlag.get(bird.CID)):
CBest[bird.CID]=bird.X
CFlag[bird.CID] = bird.Y
#便利了一遍我們得到了全局最優的種群
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
bird.CBestY=CFlag.get(bird.CID)
bird.CBestX=CBest.get(bird.CID)
def Running(self):
#這裡開始進入迭代運算
for iterate in range(1,IterationsNumber+1):
w = LinearW(iterate)
#這個算的GBestX其實始終是在算下一輪的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
CBest = {
}
CFlag = {
}
for i in range(ClusterNumber):
CFlag[i] = float("inf")
for bird in self.Population:
#更改為線性權重
self.W = w
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
# 這裡還是要無條件更細的,不然這裡的話C1就失效了
# if(y<=bird.Y):
# bird.X = x
# bird.PBestX = x
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
#個體中的最優一定包含了全局經歷過的最優值
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
if (bird.Y <= CFlag.get(bird.CID)):
CBest[bird.CID] = bird.X
CFlag[bird.CID] = bird.Y
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
bird.CBestY = CFlag.get(bird.CID)
bird.CBestX = CBest.get(bird.CID)
if __name__ == '__main__':
start = time.time()
mpso = MPSOSimple()
mpso.InitPopulation()
mpso.Running()
end = time.time()
for bird in mpso.Population:
print(bird)
print("花費時長:",end-start)
這個怎麼說呢,後者的效果相對來說還是不錯的。
原來的BasePSo
我這個是平均算的哈