This article has participated in 「 New people's creation ceremony 」 Activities , Start the road of nuggets creation together .
Statement : The copyright belongs to me , Offenders will investigate .
Please quote source for reprint https://juejin.cn/post/7111941686779412494
1.1. A recursive algorithm
1.1.1. Algorithm definition
Recursive algorithm in computer science refers to a method to solve problems by repeatedly decomposing problems into sub problems of the same kind . Simply speaking , Recursion is to call itself in the body of a method .
1.1.2. The basic idea
The essence of recursive algorithm is to decompose problems into subproblems of similar problems with reduced scale , The method is then recursively called to represent the solution to the problem . Recursive algorithms are generally used to solve three kinds of problems :
(1) The problem is defined recursively (Fibonacci function , Factorial )
(2) The solution to the problem is recursive ( Some problems can only be solved by recursion , for example , The hanotta problem )
(3) Data structures are recursive ( Linked list 、 Operation of trees, etc , Including tree traversal , Depth of tree )
Design a recursive algorithm program , Need to recognize the three elements of recursion :
(1) Reduce a problem to a smaller scale , Steps similar to mathematical induction
(2) The parent problem and the child problem cannot overlap , The parent problem can be solved by the solution of the child problem
(3) Determine the conditions for recursive termination , For example, the tree reaches the leaf node , Binary search left be equal to right
1.1.3. Code implementation -- Factorial
Problem description :
seek 6 The factorial , namely 6!=65432*1.
Algorithm analysis :
Factorials of positive integers (factorial) Is all positive integers less than or equal to this number , also 0 The factorial of is 1. Natural number n The factorial writing of n!. Define a recursive function fact, Input parameter is greater than 0, Recursively call itself in the function . The call graph is as follows :
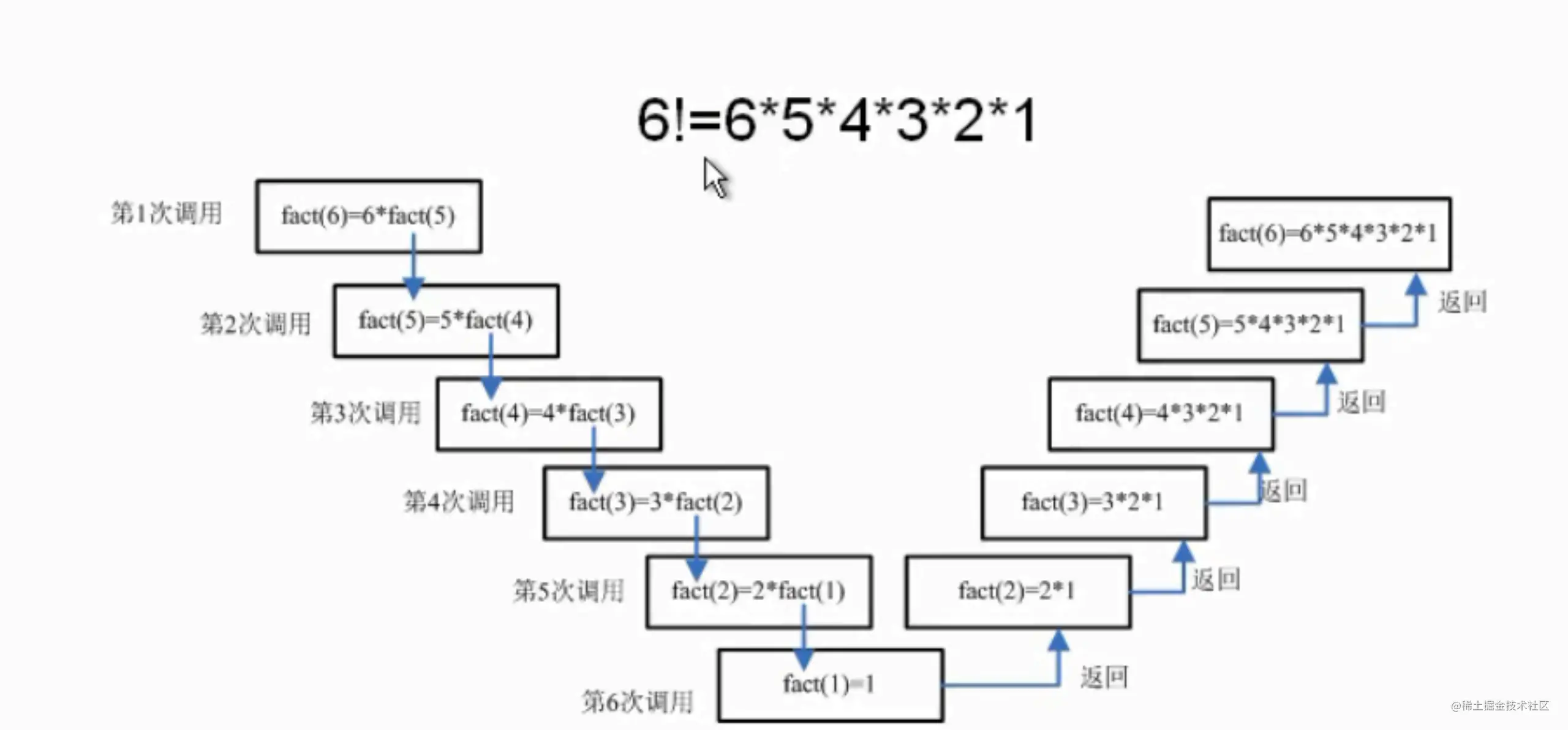
Code implementation :
【 example 1-1】 6 The factorial :
def fact(n):
result = 1
if n == 0:
return 1
else:
result = n * fact(n-1)
return result
if __name__ == '__main__':
print(fact(6))
Execution results : 720