
選自Medium,作者:Lev Maximov
機器之心編譯
支持大量多維數組和矩陣運算的 NumPy 軟件庫是許多機器學習開發者和研究者的必備工具,本文將通過直觀易懂的圖示解析常用的 NumPy 功能和函數,幫助你理解 NumPy 操作數組的內在機制。
NumPy 是一個基礎軟件庫,很多常用的 Python 數據處理軟件庫都使用了它或受到了它的啟發,包括 pandas、PyTorch、TensorFlow、Keras 等。理解 NumPy 的工作機制能夠幫助你提升在這些軟件庫方面的技能。而且在 GPU 上使用 NumPy 時,無需修改或僅需少量修改代碼。
NumPy 的核心概念是 n 維數組。n 維數組的美麗之處是大多數運算看起來都一樣,不管數組有多少維。但一維和二維有點特殊。本文分為三部分:
1. 向量:一維數組
2. 矩陣:二維數組
3. 三維及更高維
本文參考了 Jay Alammar 的文章《A Visual Intro to NumPy》並將其作為起點,然後進行了擴充,並做了一些細微修改。
NumPy 數組和 Python 列表
乍一看,NumPy 數組與 Python 列表類似。它們都可作為容器,能夠快速獲取和設置元素,但插入和移除元素會稍慢一些。
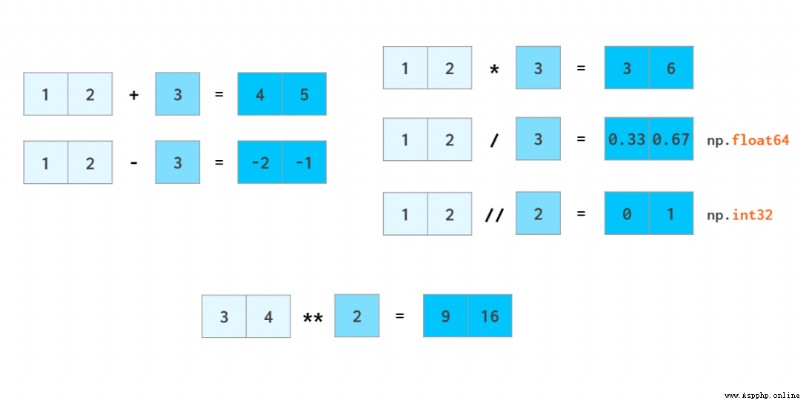
NumPy 數組完勝列表的最簡單例子是算術運算:

除此之外,NumPy 數組的優勢和特點還包括:
更緊湊,尤其是當維度大於一維時;
當運算可以向量化時,速度比列表更快;
當在後面附加元素時,速度比列表慢;
通常是同質的:當元素都是一種類型時速度很快。
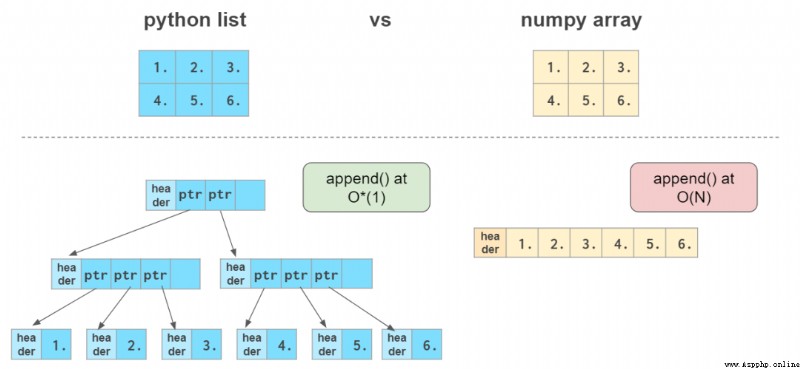
這裡 O(N) 的意思是完成該運算所需的時間和數組的大小成正比,而 O*(1)(即所謂的「均攤 O(1)」)的意思是完成運算的時間通常與數組的大小無關。
向量:一維數組
向量初始化
為了創建 NumPy 數組,一種方法是轉換 Python 列表。NumPy 數組類型可以直接從列表元素類型推導得到。

要確保向其輸入的列表是同一種類型,否則你最終會得到 dtype=’object’,這會影響速度,最終只留下 NumPy 中含有的語法糖。
NumPy 數組不能像 Python 列表一樣增長。數組的末端沒有留下任何便於快速附加元素的空間。因此,常見的做法是要麼先使用 Python 列表,准備好之後再將其轉換為 NumPy 數組,要麼是使用 np.zeros 或 np.empty 預先留下必要的空間:

通常我們有必要創建在形狀和元素類型上與已有數組匹配的空數組。

事實上,所有用於創建填充了常量值的數組的函數都帶有 _like 的形式:

NumPy 中有兩個函數能用單調序列執行數組初始化:
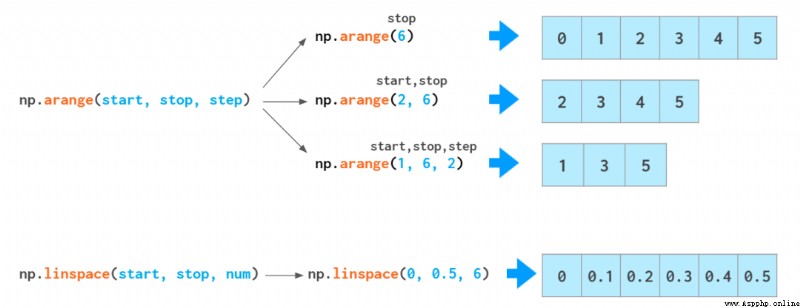
如果你需要類似 [0., 1., 2.] 這樣的浮點數數組,你可以修改 arange 輸出的類型:arange(3).astype(float),但還有一種更好的方法。arange 函數對類型很敏感:如果你以整型數作為參數輸入,它會生成整型數;如果你輸入浮點數(比如 arange(3.)),它會生成浮點數。
但 arange 並不非常擅長處理浮點數:

在我們眼裡,這個 0.1 看起來像是一個有限的十進制數,但計算機不這麼看。在二進制表示下,0.1 是一個無限分數,因此必須進行約分,也由此必然會產生誤差。也因為這個原因,如果向 arange 函數輸入帶分數部分的 step,通常得不到什麼好結果:你可能會遇到差一錯誤 (off-by-one error)。你可以使該區間的末端落在一個非整數的 step 數中(solution1),但這會降低代碼的可讀性和可維護性。這時候,linspace 就可以派上用場了。它不受捨入的影響,總能生成你要求的元素數值。不過,使用 linspace 時會遇到一個常見的陷阱:它統計的是數據點的數量,而不是區間,因此其最後一個參數 num 通常比你所想的數大 1。因此,上面最後一個例子中的數是 11,而不是 10。
在進行測試時,我們通常需要生成隨機數組:

向量索引
一旦你的數組中有了數據,NumPy 就能以非常巧妙的方式輕松地提供它們:
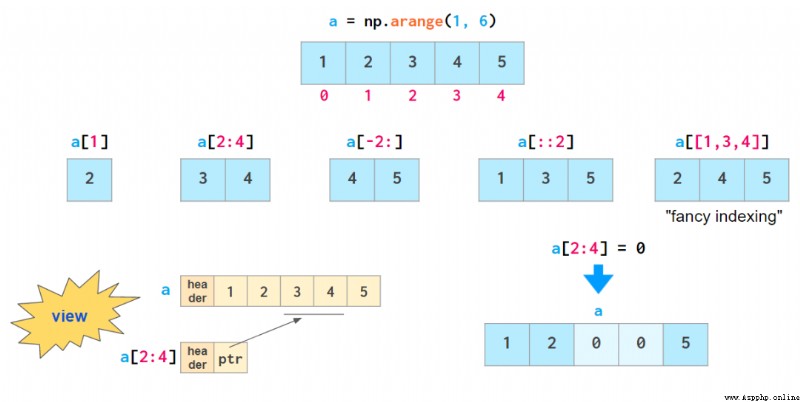
除了「花式索引(fancy indexing)」外,上面給出的所有索引方法都被稱為「view」:它們並不存儲數據,也不會在數據被索引後發生改變時反映原數組的變化情況。
所有包含花式索引的方法都是可變的:它們允許通過分配來修改原始數組的內容,如上所示。這一功能可通過將數組切分成不同部分來避免總是復制數組的習慣。

Python 列表與 NumPy 數組的對比
為了獲取 NumPy 數組中的數據,另一種超級有用的方法是布爾索引(boolean indexing),它支持使用各類邏輯運算符:
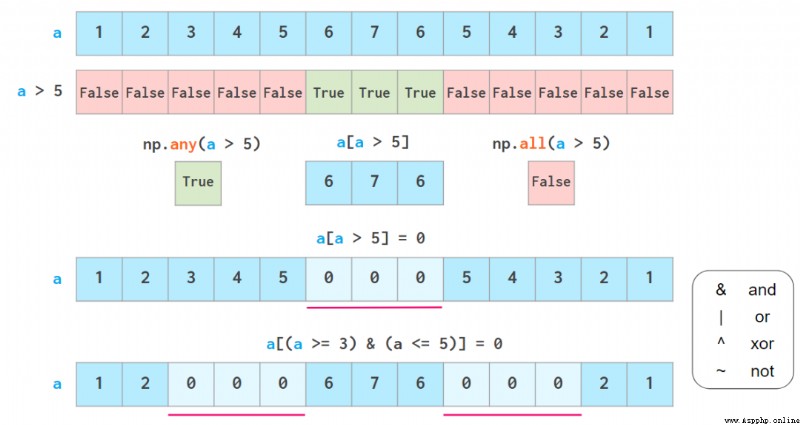
any 和 all 的作用與在 Python 中類似,但不會短路。
不過要注意,這裡不支持 Python 的「三元比較」,比如 3<=a<=5。
如上所示,布爾索引也是可寫的。其兩個常用功能都有各自的專用函數:過度重載的 np.where 函數和 np.clip 函數。它們的含義如下:
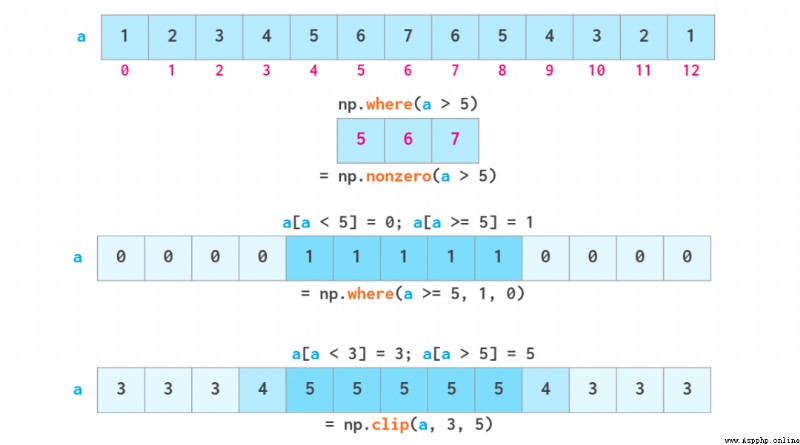
向量運算
NumPy 在速度上很出彩的一大應用領域是算術運算。向量運算符會被轉換到 C++ 層面上執行,從而避免緩慢的 Python 循環的成本。NumPy 支持像操作普通的數那樣操作整個數組。
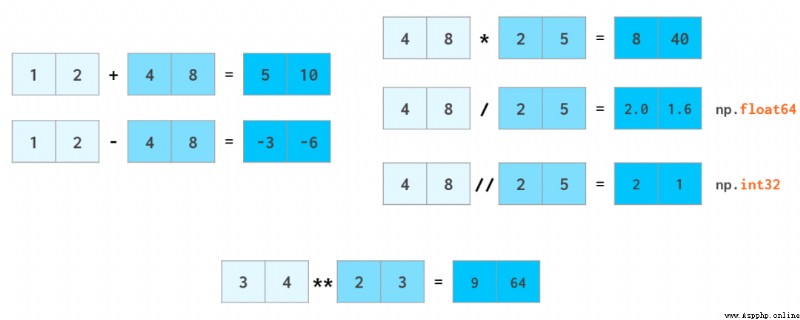
與 Python 句法一樣,a//b 表示 a 除 b(除法的商),x**n 表示 xⁿ。
正如加減浮點數時整型數會被轉換成浮點數一樣,標量也會被轉換成數組,這個過程在 NumPy 中被稱為廣播(broadcast)。
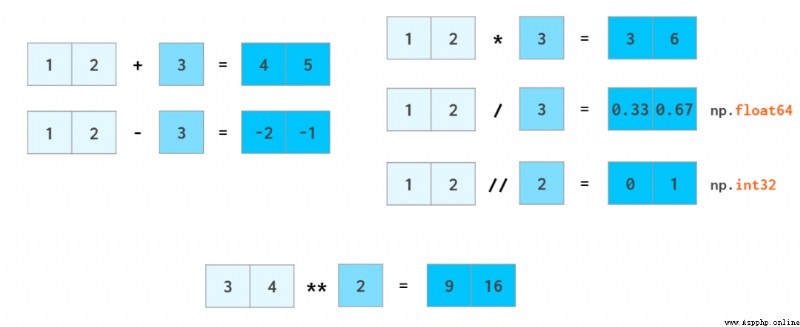
大多數數學函數都有用於處理向量的 NumPy 對應函數:
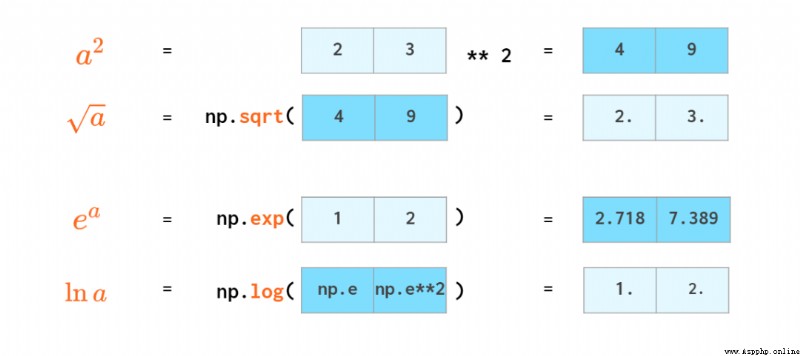
標量積有自己的運算符:
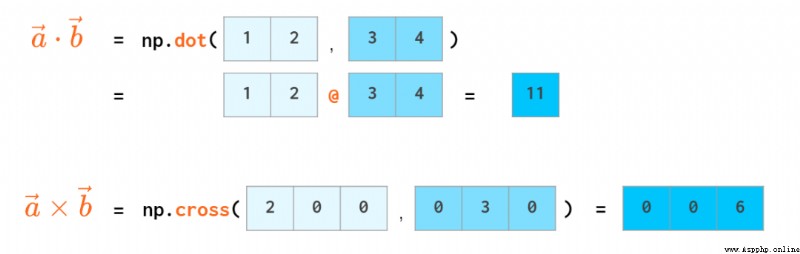
執行三角函數時也無需循環:
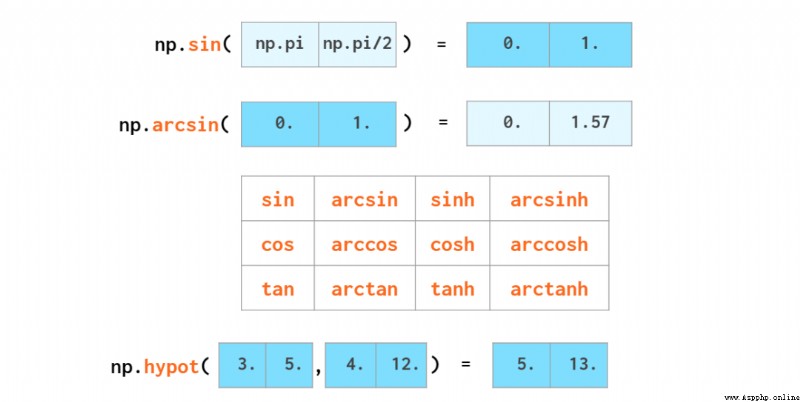
我們可以在整體上對數組進行捨入:

floor 為捨、ceil 為入,around 則是捨入到最近的整數(其中 .5 會被捨掉)
NumPy 也能執行基礎的統計運算:
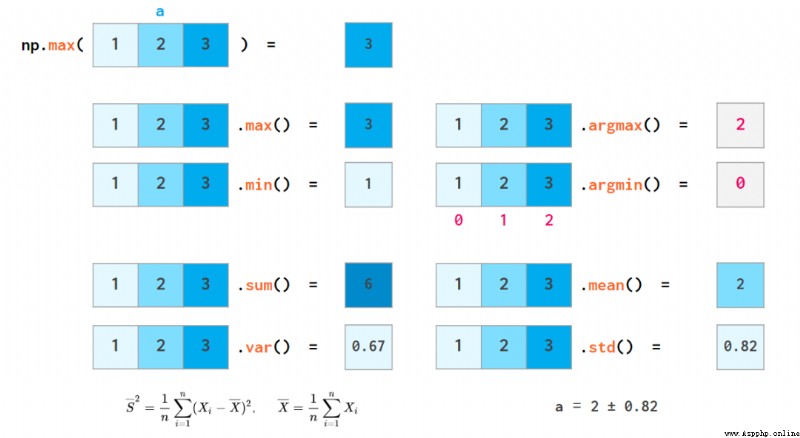
NumPy 的排序函數沒有 Python 的排序函數那麼強大:

Python 列表與 NumPy 數組的排序函數對比
在一維情況下,如果缺少 reversed 關鍵字,那麼只需簡單地對結果再執行反向,最終效果還是一樣。二維的情況則會更困難一些(人們正在請求這一功能)。
搜索向量中的元素
與 Python 列表相反,NumPy 數組沒有索引方法。人們很久之前就在請求這個功能,但一直還沒實現。
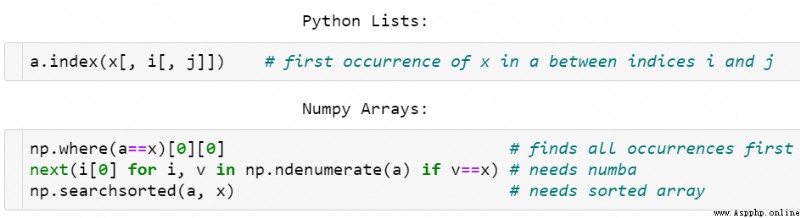
Python 列表與 NumPy 數組的對比,index() 中的方括號表示可以省略 j 或同時省略 i 和 j。
一種查找元素的方法是 np.where(a==x)[0][0],但這個方法既不優雅,速度也不快,因為它需要檢查數組中的所有元素,即便所要找的目標就在數組起始位置也是如此。
另一種更快的方式是使用 Numba 來加速 next((i[0] for i, v in np.ndenumerate(a) if v==x), -1)。
一旦數組的排序完成,搜索就容易多了:v = np.searchsorted(a, x); return v if a[v]==x else -1 的速度很快,時間復雜度為 O(log N),但它需要 O(N log N) 時間先排好序。
事實上,用 C 來實現它進而加速搜索並不是問題。問題是浮點比較。這對任何數據來說都不是一種簡單直接可用的任務。
比較浮點數
函數 np.allclose(a, b) 能在一定公差下比較浮點數數組。
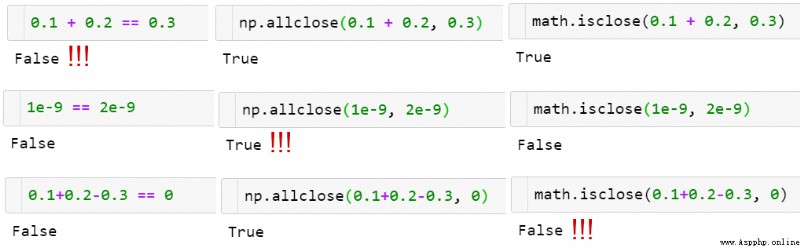
函數 np.allclose(a, b) 的工作過程示例。並沒有萬能方法!
np.allclose 假設所有被比較的數都在典型的 1 的范圍內。舉個例子,如果要在納秒級的速度內完成計算,則需要用默認的 atol 參數值除以 1e9:np.allclose(1e-9, 2e-9, atol=1e-17) == False.
math.isclose 則不會對要比較的數進行任何假設,而是依賴用戶給出合理的 abs_tol 值(對於典型的 1 的范圍內的值,取默認的 np.allclose atol 值 1e-8 就足夠好了):math.isclose(0.1+0.2–0.3, abs_tol=1e-8)==True.
除此之外,np.allclose 在絕對值和相對公差的公式方面還有一些小問題,舉個例子,對於給定的 a 和 b,存在 allclose(a, b) != allclose(b, a)。這些問題已在(標量)函數 math.isclose 中得到了解決,我們將在後面介紹它。對於這方面的更多內容,請參閱 GitHub 上的浮點數指南和對應的 NumPy 問題(https://floating-point-gui.de/errors/comparison/)。
矩陣:二維數組
NumPy 曾有一個專門的 matrix 類,但現在已經棄用了,所以本文會交替使用「矩陣」和「二維數組」這兩個術語。
矩陣的初始化句法與向量類似:

這裡必須使用雙括號,因為第二個位置參數是 dtype(可選,也接受整數)。
隨機矩陣生成的句法也與向量的類似:

二維索引的句法比嵌套列表更方便:
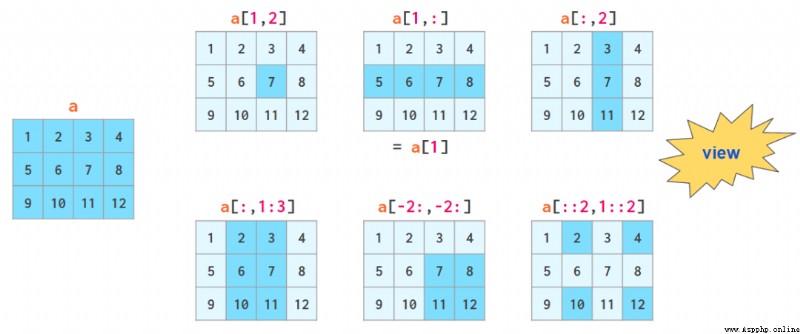
view 符號的意思是當切分一個數組時實際上沒有執行復制。當該數組被修改時,這些改變也會反映到切分得到的結果上。
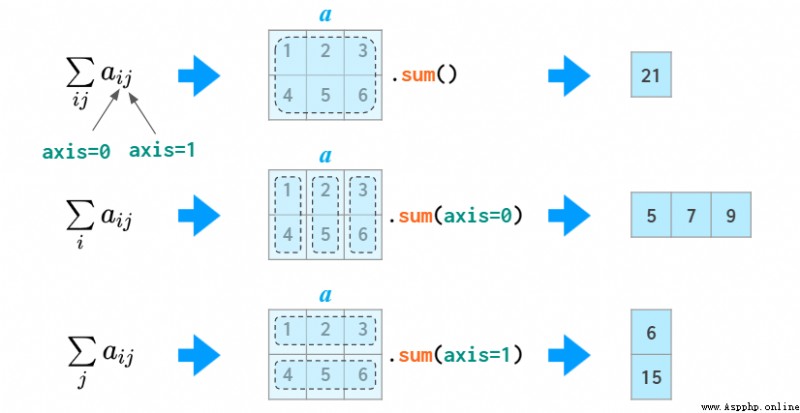
axis 參數
在很多運算中(比如 sum),你需要告訴 NumPy 是在列上還是行上執行運算。為了獲取適用於任意維度的通用符號,NumPy 引入了 axis 的概念:事實上,axis 參數的值是相關問題中索引的數量:第一個索引為 axis=0,第二個索引為 axis=1,以此類推。因此在二維情況下,axis=0 是按列計算,axis=1 是按行計算。
矩陣算術運算
除了逐元素執行的常規運算符(比如 +、-、、/、//、*),這裡還有一個計算矩陣乘積的 @ 運算符:
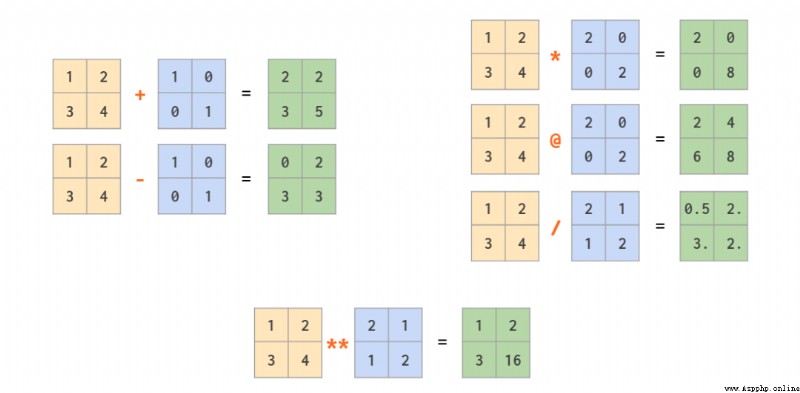
我們已在第一部分介紹過標量到數組的廣播,在其基礎上進行泛化後,NumPy 支持向量和矩陣的混合運算,甚至兩個向量之間的運算:
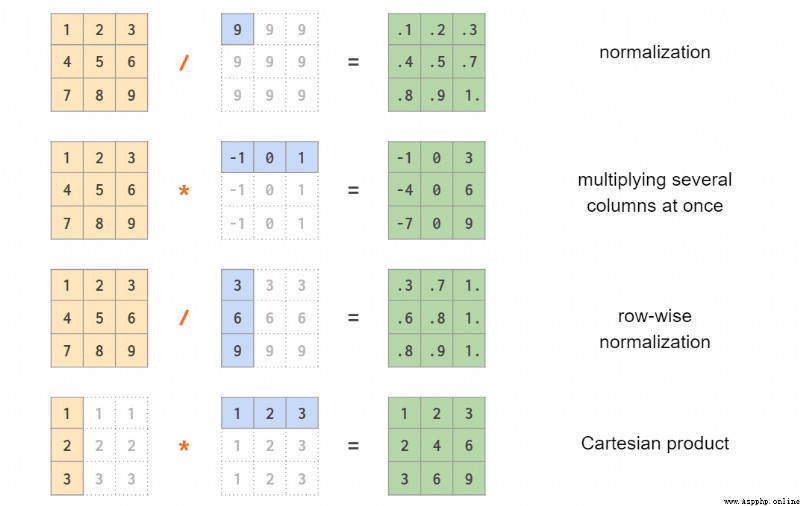
二維數組中的廣播
行向量和列向量
正如上面的例子所示,在二維情況下,行向量和列向量的處理方式有所不同。這與具備某類一維數組的 NumPy 實踐不同(比如二維數組 a— 的第 j 列 a[:,j] 是一個一維數組)。默認情況下,一維數組會被視為二維運算中的行向量,因此當用一個矩陣乘以一個行向量時,你可以使用形狀 (n,) 或 (1, n)——結果是一樣的。如果你需要一個列向量,則有多種方法可以基於一維數組得到它,但出人意料的是「轉置」不是其中之一。
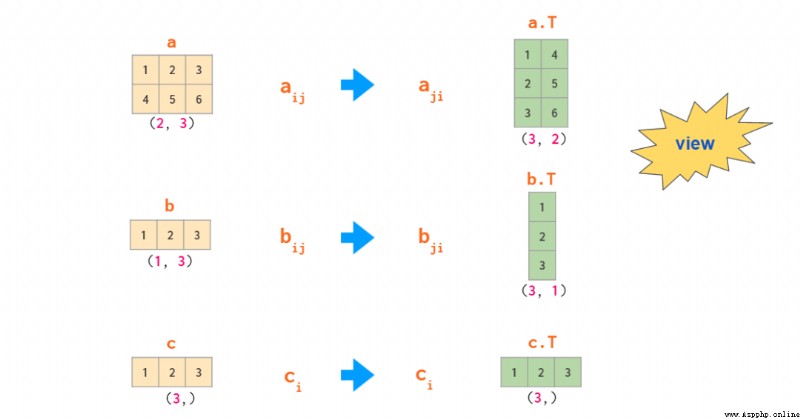
基於一維數組得到二維數組的運算有兩種:使用 reshape 調整形狀和使用 newaxis 進行索引:
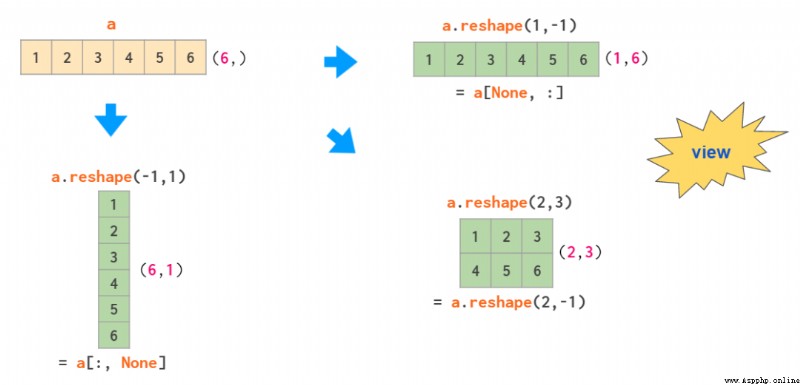
其中 -1 這個參數是告訴 reshape 自動計算其中一個維度大小,方括號中的 None 是用作 np.newaxis 的快捷方式,這會在指定位置添加一個空 axis。
因此,NumPy 共有三類向量:一維向量、二維行向量和二維列向量。下圖展示了這三種向量之間的轉換方式:
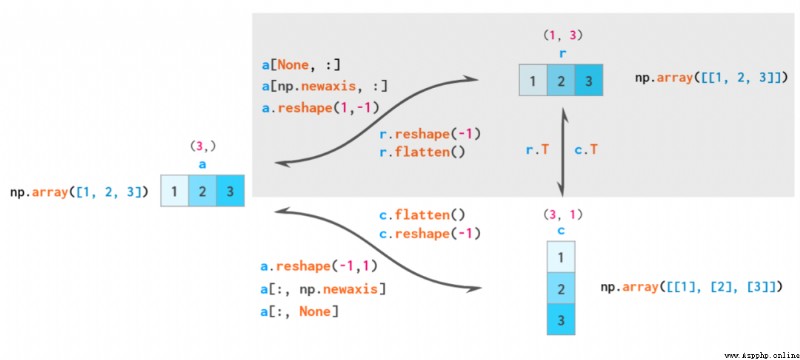
一維向量、二維行向量和二維列向量之間的轉換方式。根據廣播的原則,一維數組可被隱含地視為二維行向量,因此通常沒必要在這兩者之間執行轉換——因此相應的區域被陰影化處理。
矩陣操作
合並數組的函數主要有兩個:
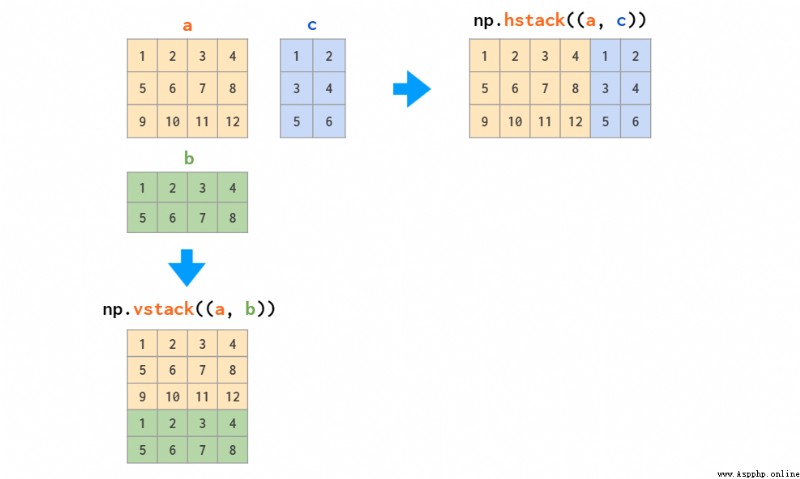
這兩個函數適用於只堆疊矩陣或只堆疊向量,但當需要堆疊一維數組和矩陣時,只有 vstack 可以奏效:hstack 會出現維度不匹配的錯誤,原因如前所述,一維數組會被視為行向量,而不是列向量。針對這個問題,解決方法要麼是將其轉換為行向量,要麼是使用能自動完成這一操作的 column_stack 函數:
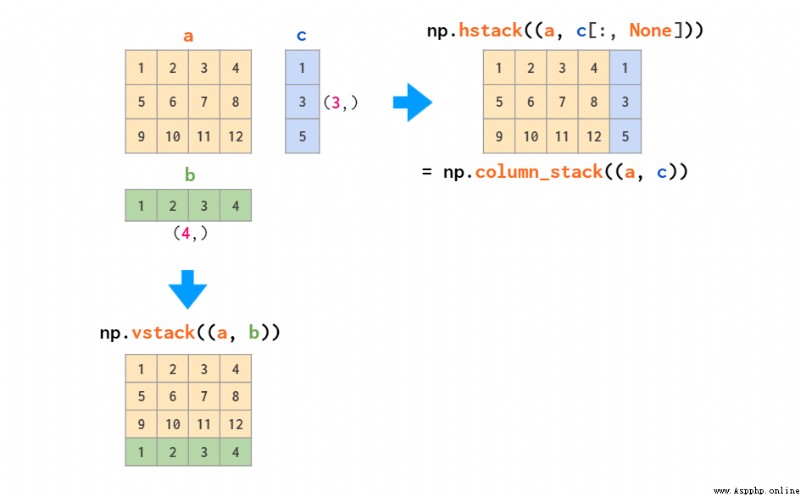
堆疊的逆操作是拆分:
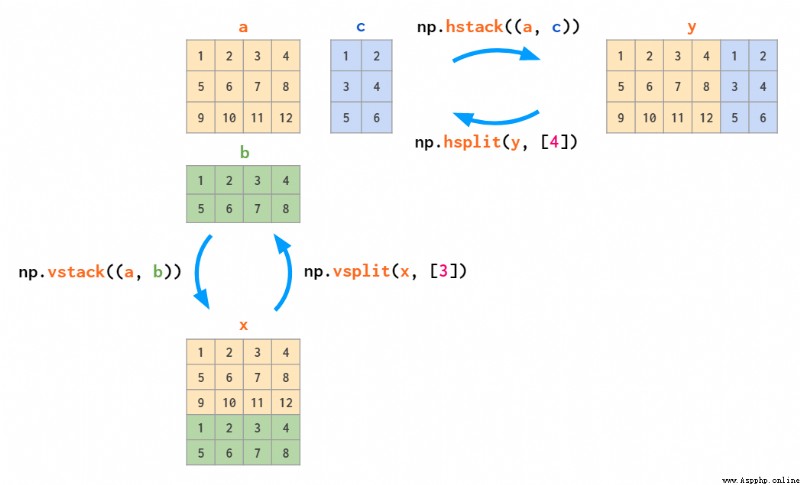
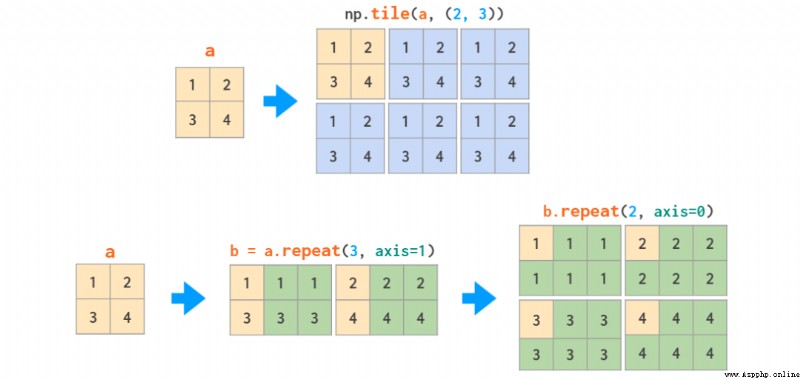
復制矩陣的方法有兩種:復制 - 粘貼式的 tile 和分頁打印式的 repeat:
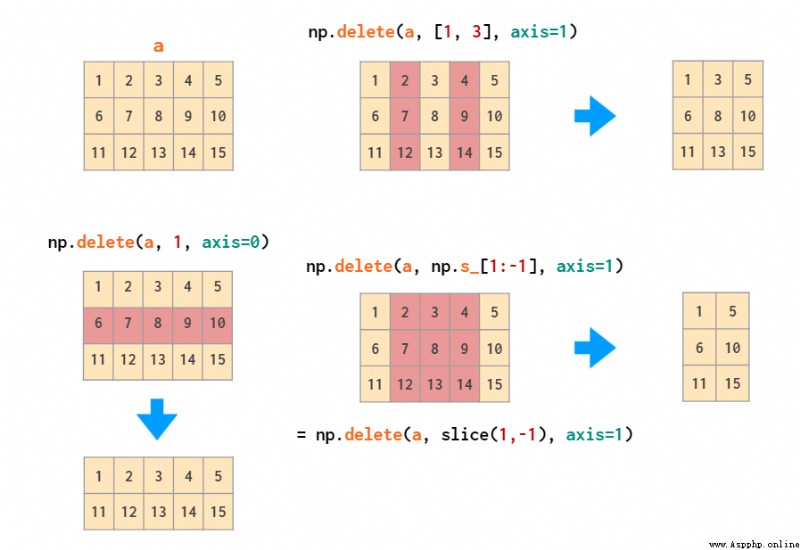
delete 可以刪除特定的行和列:
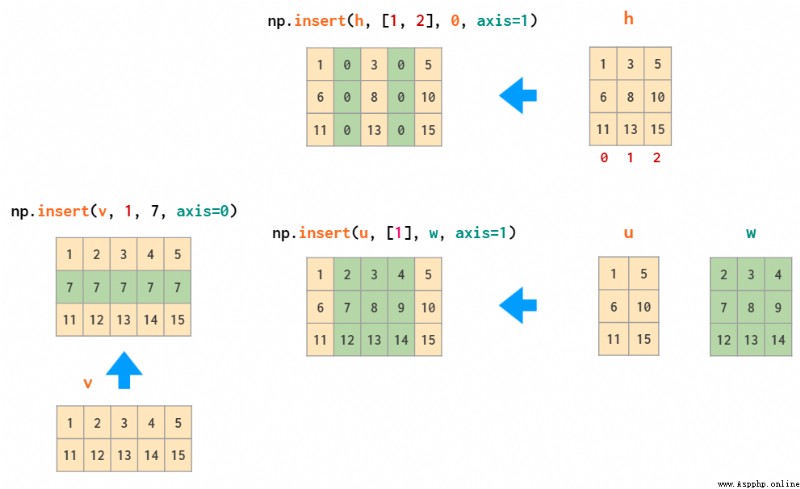
刪除的逆操作為插入,即 insert:
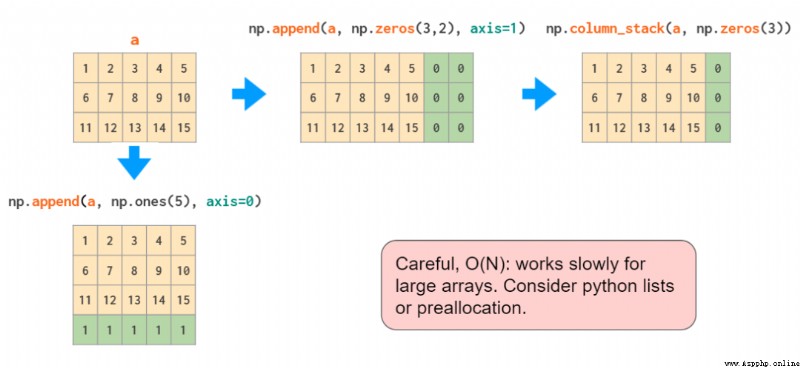
append 函數就像 hstack 一樣,不能自動對一維數組執行轉置,因此同樣地,要麼需要改變該向量的形狀,要麼就需要增加一個維度,或者使用 column_stack:
事實上,如果你只需要向數組的邊緣添加常量值,那麼(稍微復雜的)pad 函數應該就足夠了:
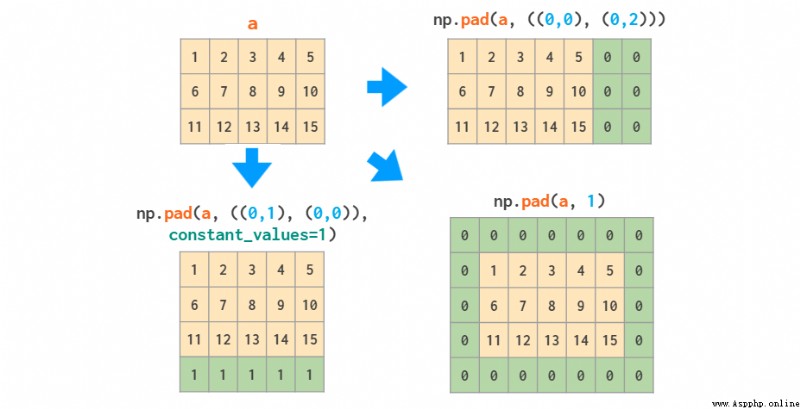
網格
廣播規則使得我們能更簡單地操作網格。假設你有如下矩陣(但非常大):

使用 C 和使用 Python 創建矩陣的對比
這兩種方法較慢,因為它們會使用 Python 循環。為了解決這樣的問題,MATLAB 的方式是創建一個網格:
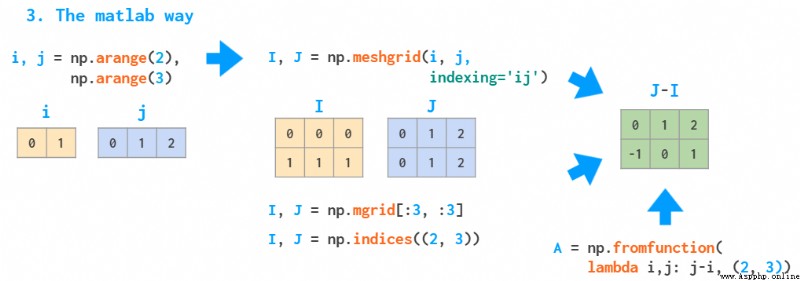
使用 MATLAB 創建網格的示意圖
使用如上提供的參數 I 和 J,meshgrid 函數接受任意的索引集合作為輸入,mgrid 只是切分,indices 只能生成完整的索引范圍,fromfunction 只會調用所提供的函數一次。
但實際上,NumPy 中還有一種更好的方法。我們沒必要將內存耗在整個 I 和 J 矩陣上。存儲形狀合適的向量就足夠了,廣播規則可以完成其余工作。

使用 NumPy 創建網格的示意圖
沒有 indexing=’ij’ 參數,meshgrid 會改變這些參數的順序:J, I= np.meshgrid(j, i)——這是一種 xy 模式,對可視化 3D 圖表很有用。
獲取矩陣統計數據
和 sum 一樣,min、max、argmin、argmax、mean、std、var 等所有其它統計函數都支持 axis 參數並能據此完成統計計算:
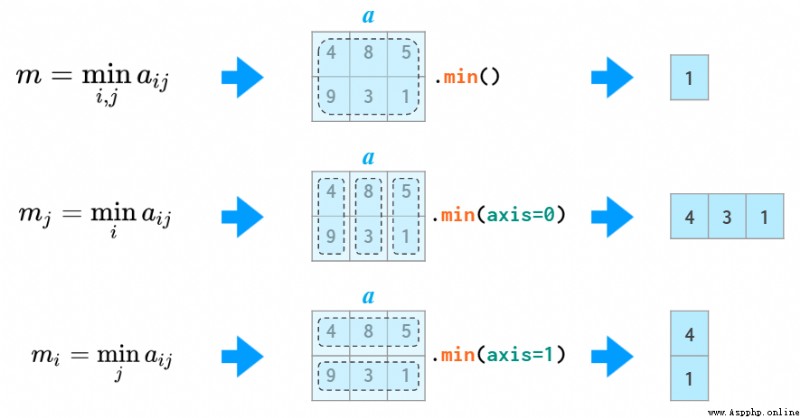
三個統計函數示例,為了避免與 Python 的 min 沖突,NumPy 中對應的函數名為 np.amin。
用於二維及更高維的 argmin 和 argmax 函數會返回最小和最大值的第一個實例,在返回展開的索引上有點麻煩。為了將其轉換成兩個坐標,需要使用 unravel_index 函數:
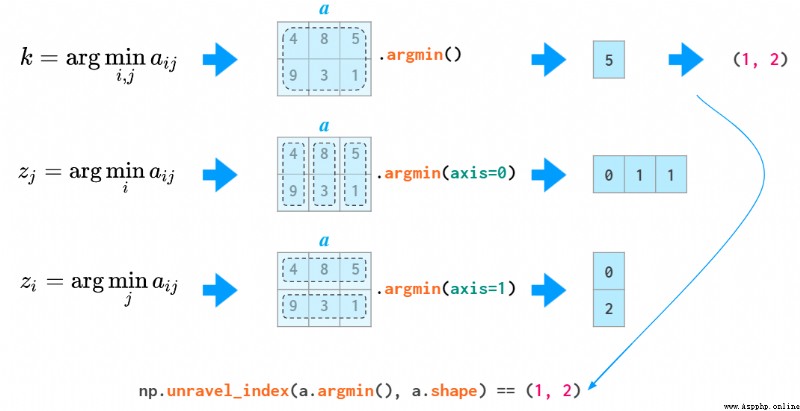
使用 unravel_index 函數的示例
all 和 any 函數也支持 axis 參數:
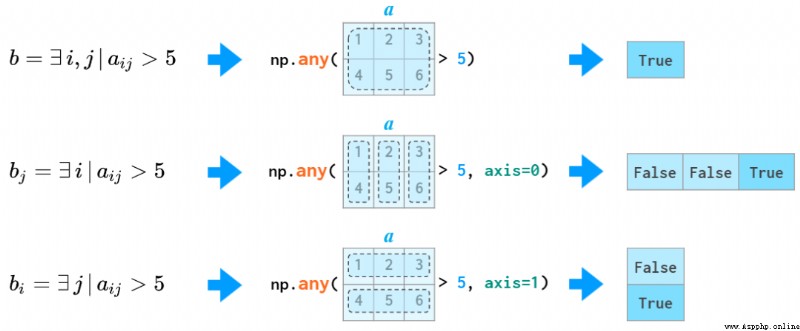
使用 all 和 any 函數的示例
矩陣排序
axis 參數雖然對上面列出的函數很有用,但對排序毫無用處:

使用 Python 列表和 NumPy 數組執行排序的比較
這通常不是你在排序矩陣或電子表格時希望看到的結果:axis 根本不能替代 key 參數。但幸運的是,NumPy 提供了一些支持按列排序的輔助函數——或有需要的話可按多列排序:
1. a[a[:,0].argsort()] 可按第一列對數組排序:
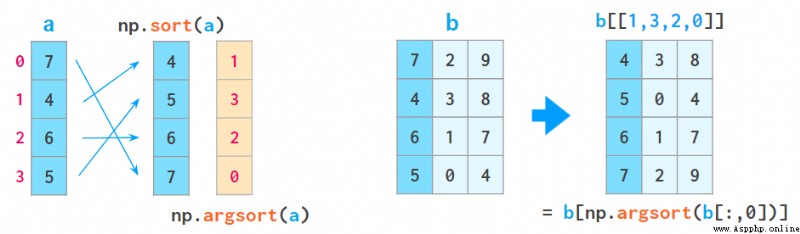
這裡 argsort 會返回原數組排序後的索引的數組。
這個技巧可以重復,但必須謹慎,別讓下一次排序擾亂上一次排序的結果:
a = a[a[:,2].argsort()]
a = a[a[:,1].argsort(kind='stable')]
a = a[a[:,0].argsort(kind='stable')]
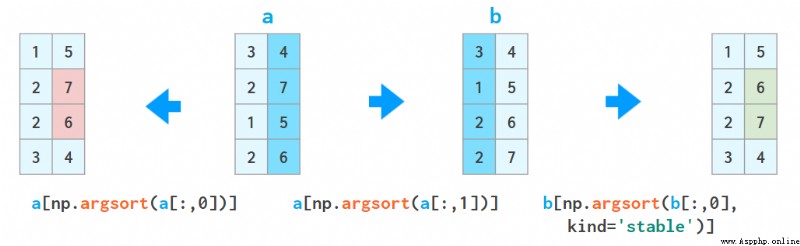
2. lexsort 函數能使用上述方式根據所有列進行排序,但它總是按行執行,而且所要排序的行的順序是反向的(即自下而上),因此使用它時會有些不自然,比如
- a[np.lexsort(np.flipud(a[2,5].T))] 會首先根據第 2 列排序,然後(當第 2 列的值相等時)再根據第 5 列排序。
– a[np.lexsort(np.flipud(a.T))] 會從左向右根據所有列排序。
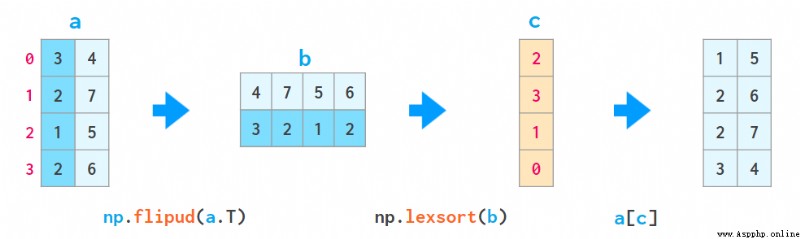
這裡,flipud 會沿上下方向翻轉該矩陣(准確地說是 axis=0 方向,與 a[::-1,...] 一樣,其中三個點表示「所有其它維度」,因此翻轉這個一維數組的是突然的 flipud,而不是 fliplr。
3. sort 還有一個 order 參數,但如果一開始是普通的(非結構化)數組,它執行起來既不快,也不容易使用。
4. 在 pandas 中執行它可能是更好的選擇,因為在 pandas 中,該特定運算的可讀性要高得多,也不那麼容易出錯:
– pd.DataFrame(a).sort_values(by=[2,5]).to_numpy() 會先根據第 2 列排序,然後根據第 5 列排序。
– pd.DataFrame(a).sort_values().to_numpy() 會從左向右根據所有列排序。
三維及更高維
當你通過調整一維向量的形狀或轉換嵌套的 Python 列表來創建 3D 數組時,索引的含義是 (z,y,x)。第一個索引是平面的數量,然後是在該平面上的坐標:
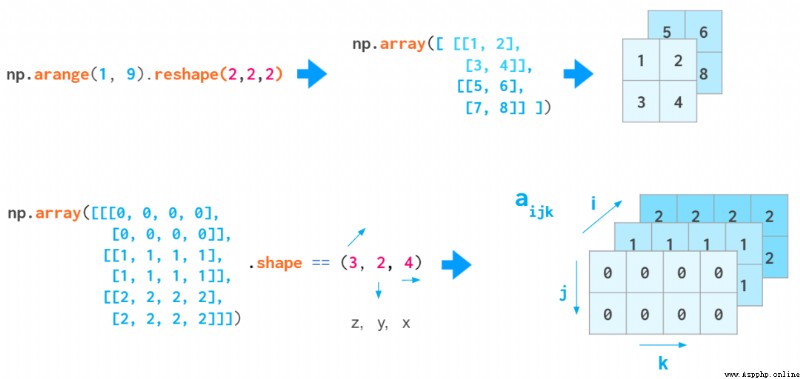
展示 (z,y,x) 順序的示意圖
這個索引順序很方便,舉個例子,它可用於保存一些灰度圖像:a[i] 是索引第 i 張圖像的快捷方式。
但這個索引順序不是通用的。當操作 RGB 圖像時,通常會使用 (y,x,z) 順序:首先是兩個像素坐標,最後一個是顏色坐標(Matplotlib 中是 RGB,OpenCV 中是 BGR):
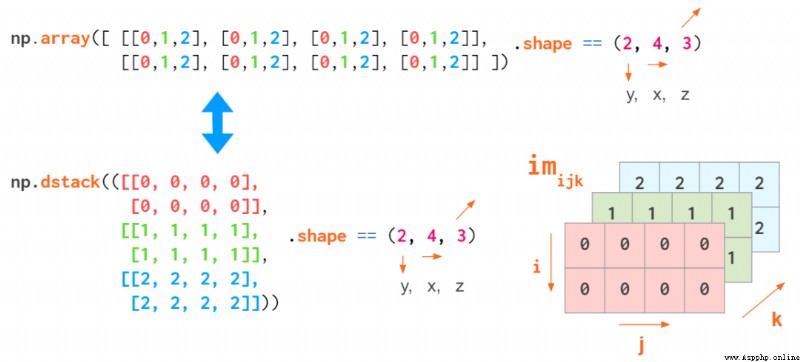
展示 (y,x,z) 順序的示意圖
這樣,我們就能很方便地索引特定的像素:a[i,j] 能提供 (i,j) 位置的 RGB 元組。
因此,創建幾何形狀的實際命令取決於你所在領域的慣例:
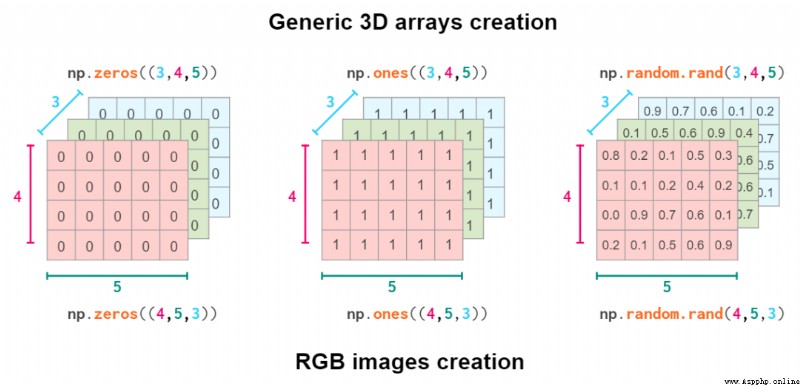
創建一般的三維數組和 RGB 圖像
很顯然,hstack、vstack、dstack 這些函數不支持這些慣例。它們硬編碼了 (y,x,z) 的索引順序,即 RGB 圖像的順序:
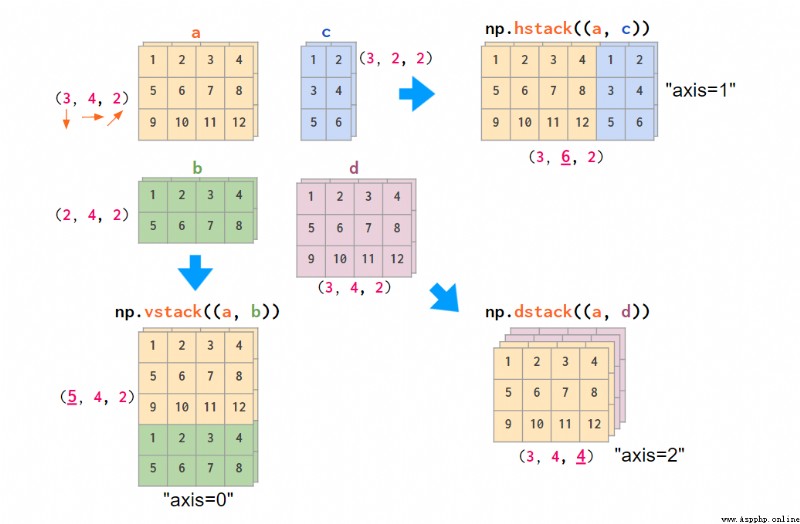
NumPy 使用 (y,x,z) 順序的示意圖,堆疊 RGB 圖像(這裡僅有兩種顏色)
如果你的數據布局不同,使用 concatenate 命令來堆疊圖像會更方便一些,向一個 axis 參數輸入明確的索引數值:
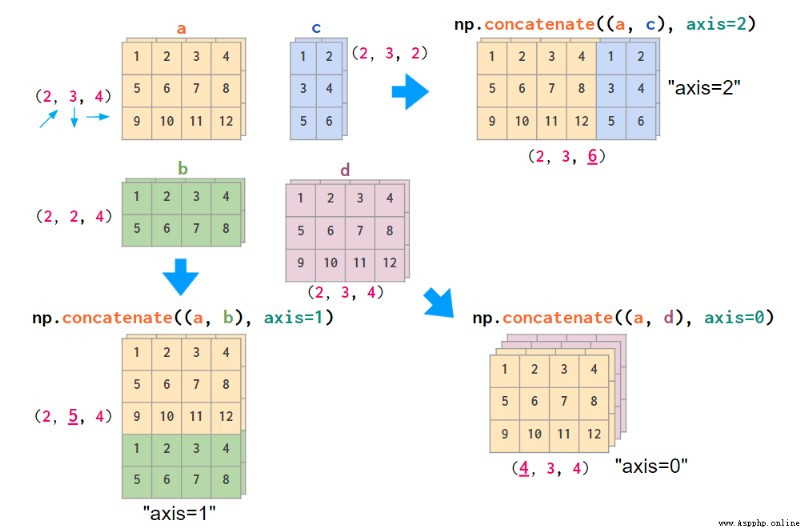
堆疊一般三維數組
如果你不習慣思考 axis 數,你可以將該數組轉換成 hstack 等函數中硬編碼的形式:
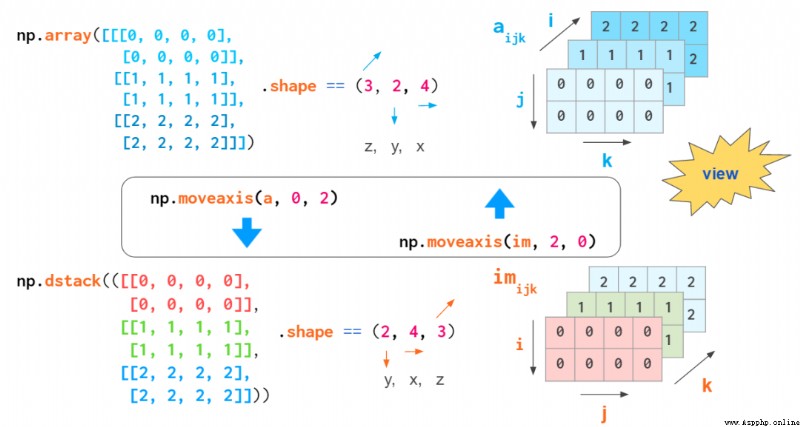
將數組轉換為 hstack 中硬編碼的形式的示意圖
這種轉換的成本很低:不會執行實際的復制,只是執行過程中混合索引的順序。
另一種可以混合索引順序的運算是數組轉置。了解它可能會讓你更加熟悉三維數組。根據你決定使用的 axis 順序的不同,轉置數組所有平面的實際命令會有所不同:對於一般數組,它會交換索引 1 和 2,對 RGB 圖像而言是 0 和 1:
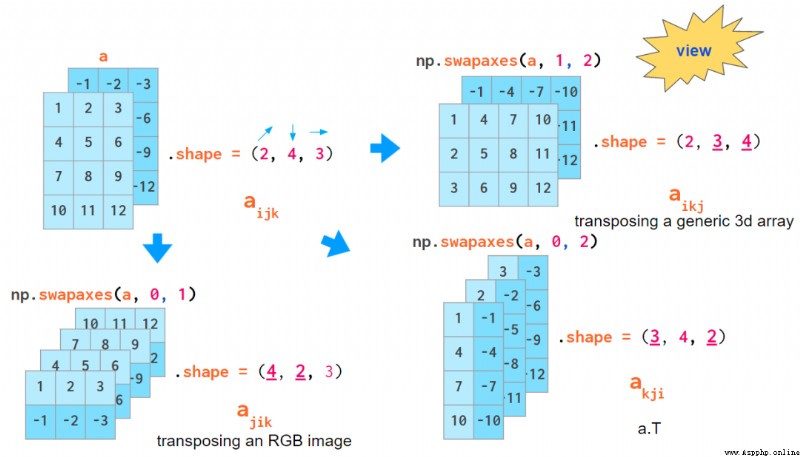
轉置一個三維數據的所有平面的命令
不過有趣的是,transpose 的默認 axes 參數(以及僅有的 a.T 運算模式)會調轉索引順序的方向,這與上述兩個索引順序慣例都不相符。
最後,還有一個函數能避免你在處理多維數組時使用太多訓練,還能讓你的代碼更簡潔——einsum(愛因斯坦求和):

它會沿重復的索引對數組求和。在這個特定的例子中,np.tensordot(a, b, axis=1) 足以應對這兩種情況,但在更復雜的情況中,einsum 的速度可能更快,而且通常也更容易讀寫——只要你理解其背後的邏輯。
如果你希望測試你的 NumPy 技能,GitHub 有 100 道相當困難的練習題:https://github.com/rougier/numpy-100。
你最喜歡的 NumPy 功能是什麼?請與我們分享!
原文鏈接:https://medium.com/better-programming/numpy-illustrated-the-visual-guide-to-numpy-3b1d4976de1d
往期精彩回顧
適合初學者入門人工智能的路線及資料下載(圖文+視頻)機器學習入門系列下載中國大學慕課《機器學習》(黃海廣主講)機器學習及深度學習筆記等資料打印《統計學習方法》的代碼復現專輯機器學習交流qq群955171419,加入微信群請掃碼