
selected from Medium, author :Lev Maximov
Heart of machine compilation
Support a large number of multidimensional array and matrix operations NumPy Software library is a necessary tool for many machine learning developers and researchers , In this paper, we will analyze the commonly used NumPy Functions and functions , To help you understand NumPy The intrinsic mechanism of manipulating arrays .
NumPy It's a basic software library , A lot of common Python It's inspired by the software that processes the data , Include pandas、PyTorch、TensorFlow、Keras etc. . understand NumPy The working mechanism of can help you improve your skills in these software libraries . And in GPU Upper use NumPy when , There is no need to modify or just a small amount of code modification .
NumPy The core concept of n Dimension group .n The beauty of dimension sets is that most operations look the same , No matter how many dimensions an array has . But one and two dimensions are a little special . This article is divided into three parts :
1. vector : One dimensional array
2. matrix : Two dimensional array
3. Three dimensions and higher
This paper refers to Jay Alammar The article 《A Visual Intro to NumPy》 And use it as a starting point , And then it expanded , And made some minor changes .
NumPy Array and Python list
At first glance ,NumPy An array with the Python The list is similar to . They all serve as containers , Can quickly get and set elements , But inserting and removing elements is a little slower .
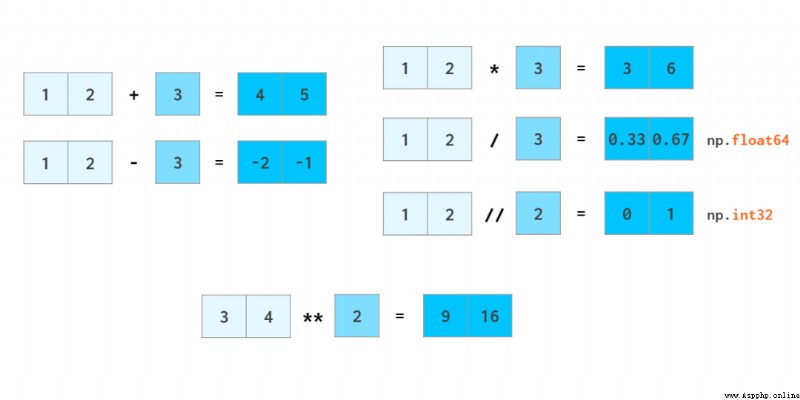
NumPy The simplest example of an array winning list is arithmetic :

besides ,NumPy The advantages and characteristics of arrays also include :
More compact , Especially when the dimension is larger than one dimension ;
When the operation can be vectorized , Faster than lists ;
When you attach elements to the back , Slower than the list ;
Usually homogeneous : It's fast when all elements are of one type .
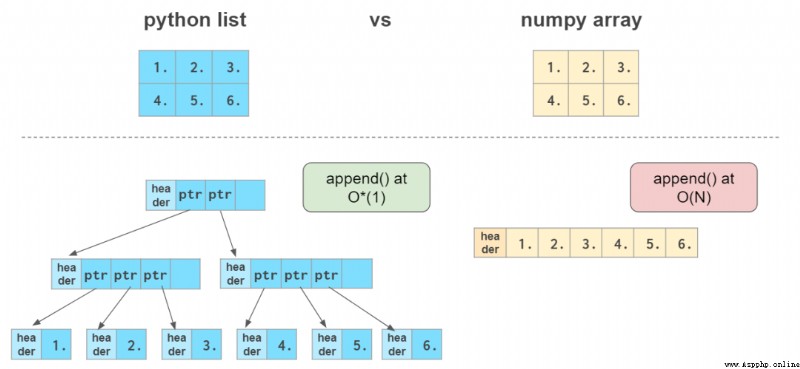
here O(N) The time required to complete the operation is proportional to the size of the array , and O*(1)( That is to say 「 capitation O(1)」) The time to complete an operation is usually independent of the size of the array .
vector : One dimensional array
Vector initialization
In order to create NumPy Array , One way is to transform Python list .NumPy Array types can be derived directly from list element types .

Make sure that the list you enter is of the same type , Or you'll end up with dtype=’object’, It affects speed , In the end, only NumPy The grammar sugar contained in .
NumPy Arrays can't be like Python It's growing like a list . There is no space left at the end of the array to quickly attach elements . therefore , The common practice is to either use Python list , When you're ready, convert it to NumPy Array , Or use np.zeros or np.empty Leave the necessary space in advance :

Usually it is necessary to create an empty array that matches an existing array in shape and element type .

in fact , All functions used to create arrays filled with constant values have _like In the form of :

NumPy Two functions in can perform array initialization with a monotone sequence :
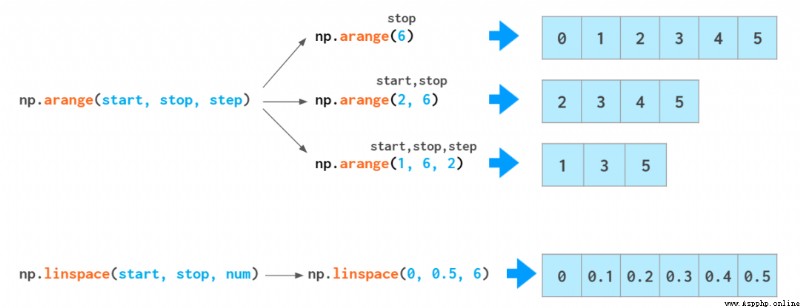
If you need something like that [0., 1., 2.] Such an array of floating-point numbers , You can modify arange Type of output :arange(3).astype(float), But there's a better way .arange Functions are type sensitive : If you enter an integer as a parameter , It generates integers ; If you enter a floating-point number ( such as arange(3.)), It generates floating-point numbers .
but arange Not very good at dealing with floating-point numbers :

In our eyes , This 0.1 It looks like a finite decimal number , But computers don't see it that way . In binary representation ,0.1 It's an infinite fraction , So we have to make a reduction , It will inevitably lead to errors . And for this reason , If to arange Function input with fractional part step, It usually doesn't get good results : You may come across a mistake (off-by-one error). You can make the end of the interval fall on a non integer step In number (solution1), But it reduces the readability and maintainability of the code . Now ,linspace I can use it . It's not affected by rounding , Always generate the element values you want . however , Use linspace There's a common pitfall that you'll encounter when you're on the road : It counts the number of data points , Not intervals , So the last parameter num Usually more than you think 1. therefore , The number in the last example above is 11, instead of 10.
When testing , We usually need to generate random arrays :

Vector index
Once you have data in your array ,NumPy They can be easily provided in a very clever way :
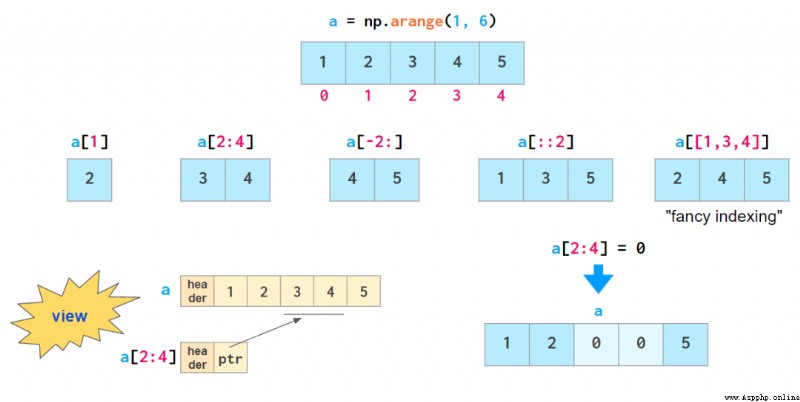
except 「 Fancy index (fancy indexing)」 Outside , All the indexing methods given above are called 「view」: They don't store data , It will not reflect the changes of the original array when the data is indexed .
All methods that include fancy indexes are variable : They allow the contents of the original array to be modified by assignment , As shown above . This feature avoids the habit of always copying arrays by splitting them into different parts .

Python List and NumPy Comparison of arrays
In order to obtain NumPy Data in array , Another super useful method is Boolean index (boolean indexing), It supports the use of all kinds of logical operators :
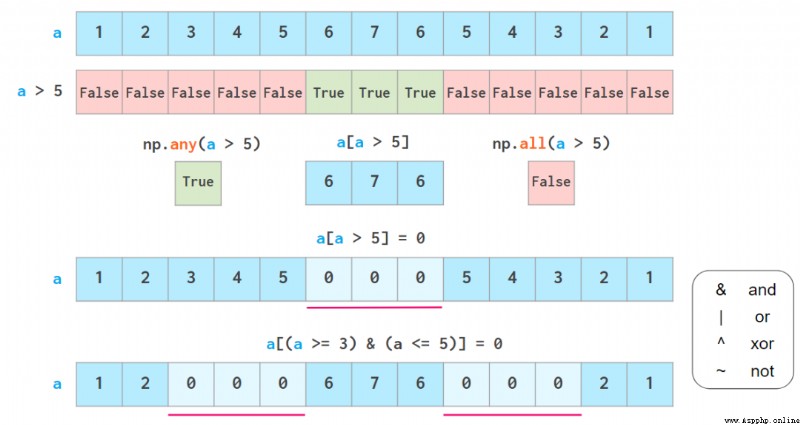
any and all The role of and in Python It's similar to , But no short circuit .
But be careful , Not supported here Python Of 「 Ternary comparison 」, such as 3<=a<=5.
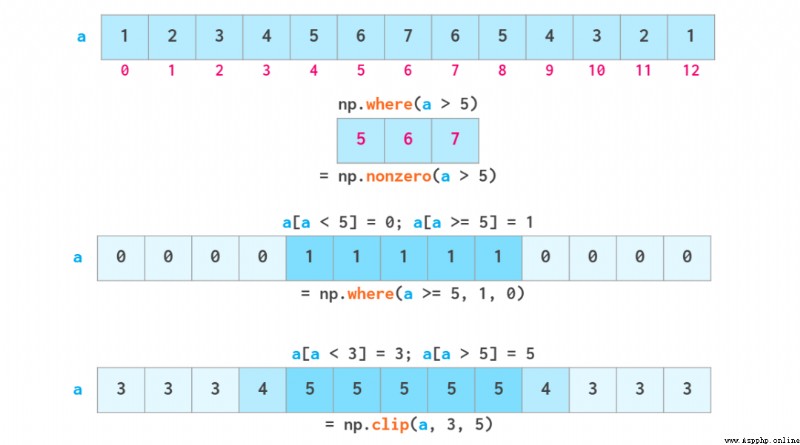
As shown above , Boolean indexes are also writable . Its two common functions have their own special functions : Overloaded np.where Functions and np.clip function . Their meanings are as follows :
Vector operations
NumPy One of the great applications of speed is arithmetic . Vector operators are converted to C++ At the level of execution , So as to avoid slow Python The cost of recycling .NumPy Support the operation of the entire array just like the operation of ordinary numbers .
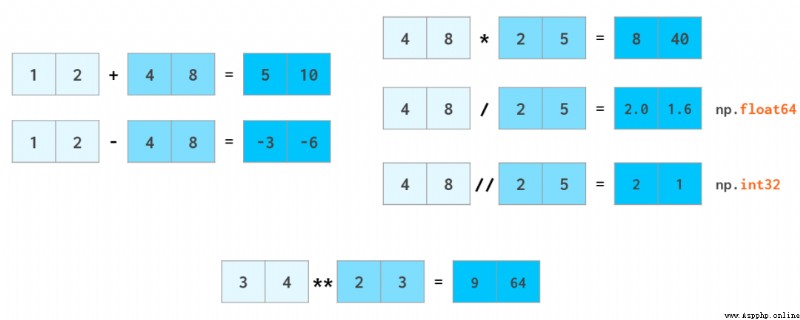
And Python Syntax is the same ,a//b Express a except b( The quotient of division ),x**n Express xⁿ.
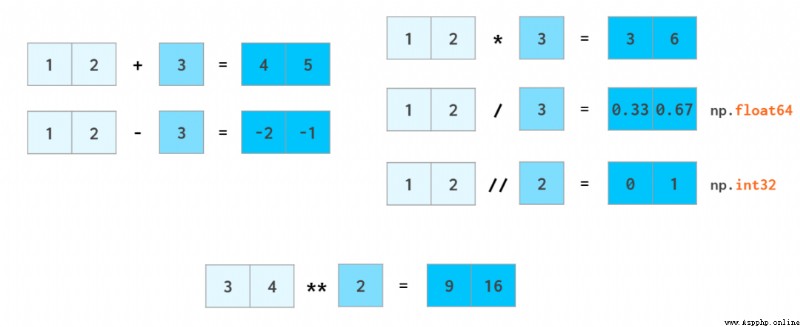
Just like adding and subtracting floating-point numbers, integer numbers are converted to floating-point numbers , Scalars are also converted to arrays , This process takes place in NumPy It's called broadcasting (broadcast).
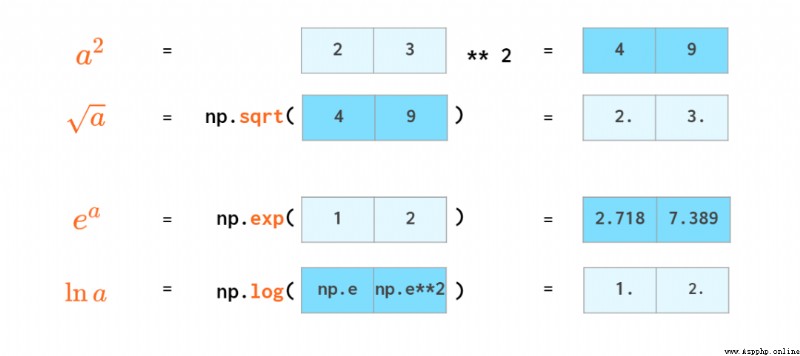
Most mathematical functions have functions for dealing with vectors NumPy The corresponding function :
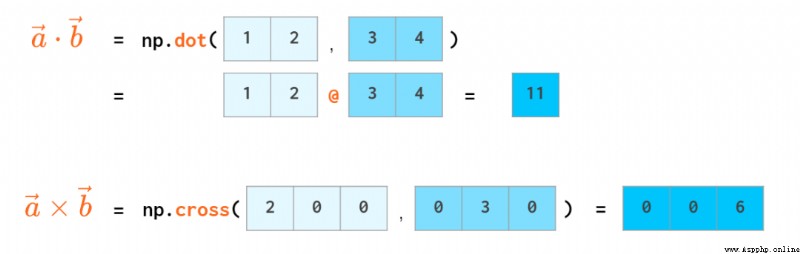
Scalar products have their own operators :
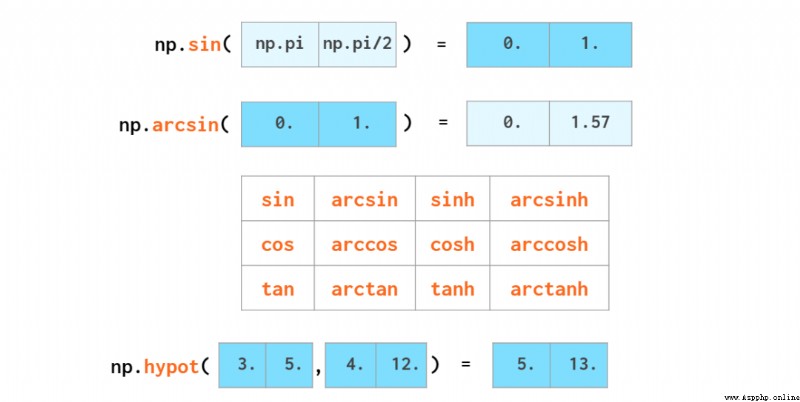
You don't have to loop to perform trigonometric functions :
We can round the array as a whole :

floor To give up 、ceil In order to enter ,around Is rounded to the nearest integer ( among .5 Will be abandoned )
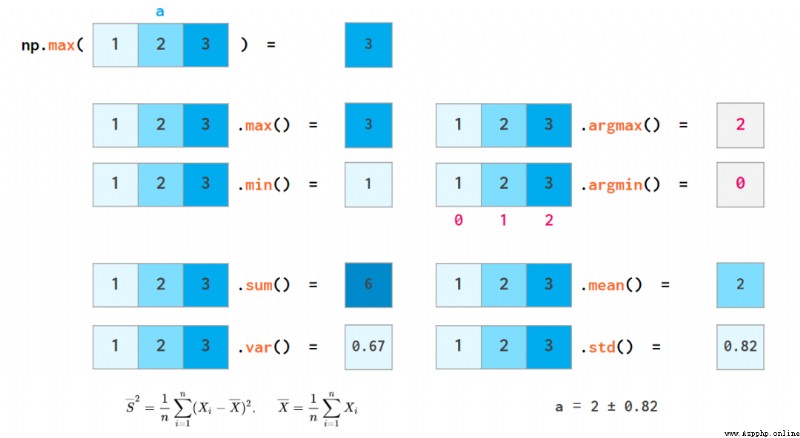
NumPy Can also perform basic statistical operations :
NumPy The sort function of does not have Python The sorting function is so powerful :

Python List and NumPy Array sorting function comparison
In the case of one dimension , If there is a lack of reversed keyword , Then simply reverse the result , The end result is the same . The two-dimensional case is more difficult ( People are asking for this function ).
Search for elements in a vector
And Python The list is the opposite ,NumPy Array has no index method . People have been asking for this function for a long time , But it hasn't come true yet .
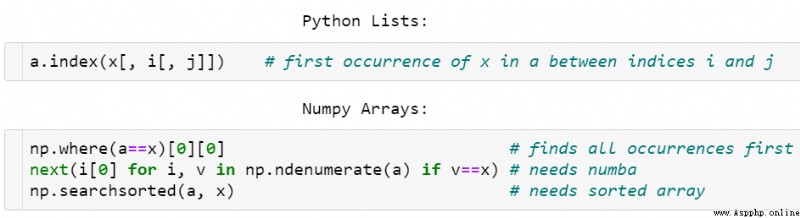
Python List and NumPy Comparison of arrays ,index() The square brackets in can be omitted j Or omit at the same time i and j.
One way to find elements is np.where(a==x)[0][0], But this approach is neither elegant , Not fast either , Because it needs to check all the elements in the array , Even if the target is at the beginning of the array .
Another way to use it is faster Numba To speed up next((i[0] for i, v in np.ndenumerate(a) if v==x), -1).
Once the array is sorted , It's much easier to search :v = np.searchsorted(a, x); return v if a[v]==x else -1 It's very fast , The time complexity is O(log N), But it needs O(N log N) Time first .
in fact , use C It's not a problem to implement it and speed up the search . The problem is floating point comparisons . This is not a simple and directly available task for any data .
Compare floating-point numbers
function np.allclose(a, b) Can compare floating-point number array under certain tolerance .
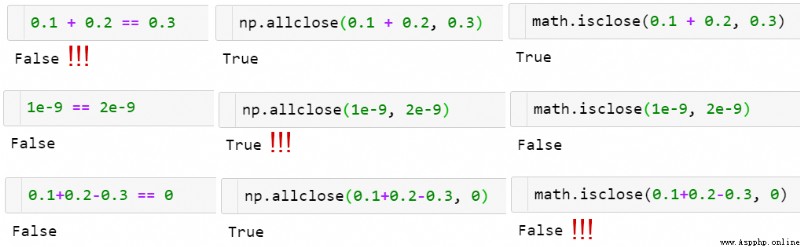
function np.allclose(a, b) Example of working process of . There is no universal way !
np.allclose Suppose that all the numbers being compared are in the typical 1 Within the scope of . for instance , If you want to complete the calculation in nanoseconds , You need to use the default atol The parameter value is divided by 1e9:np.allclose(1e-9, 2e-9, atol=1e-17) == False.
math.isclose No assumptions are made about the number to be compared , It depends on the user to give a reasonable abs_tol value ( For typical 1 Values in the range of , Take the default np.allclose atol value 1e-8 That's good enough ):math.isclose(0.1+0.2–0.3, abs_tol=1e-8)==True.
besides ,np.allclose There are still some small problems in the formula of absolute value and relative tolerance , for instance , For a given a and b, There is allclose(a, b) != allclose(b, a). These questions are already in ( Scalar ) function math.isclose It has been solved , We'll talk about it later . For more on this , see also GitHub Floating point guide on and the corresponding NumPy problem (https://floating-point-gui.de/errors/comparison/).
matrix : Two dimensional array
NumPy There was a special matrix class , But now it's abandoned , So this article will alternate 「 matrix 」 and 「 Two dimensional array 」 These two terms .
The initialization syntax of a matrix is similar to that of a vector :
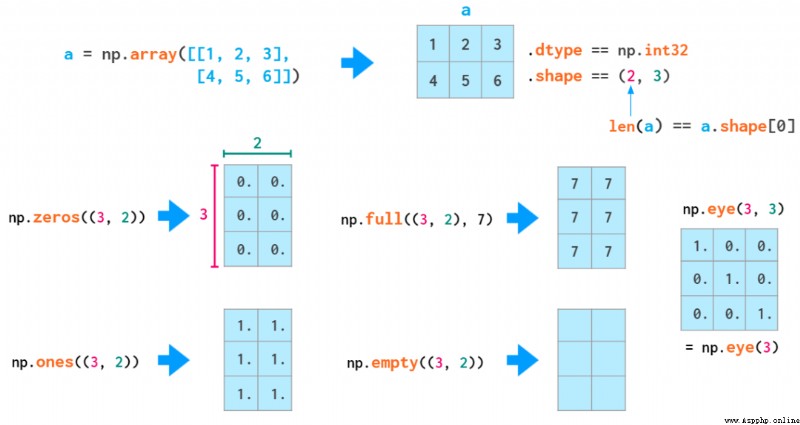
You have to use double brackets here , Because the second positional parameter is dtype( Optional , Also accept integers ).
The syntax of random matrix generation is similar to that of vector generation :

The syntax of two-dimensional index is more convenient than nested list :
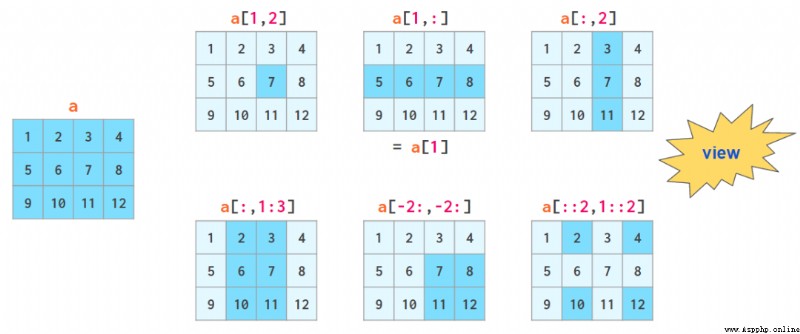
view The symbol means that when you slice an array, you don't actually copy it . When the array is modified , These changes will also be reflected in the segmentation results .
axis Parameters
In many operations ( such as sum), You need to tell NumPy Whether the operation is performed on a column or a row . In order to obtain a general symbol suitable for any dimension ,NumPy Introduced axis The concept of : in fact ,axis The value of the parameter is the number of indexes in the related problem : The first index is axis=0, The second index is axis=1, And so on . So in two dimensions ,axis=0 It's in columns ,axis=1 It's by line .

Matrix arithmetic operation
In addition to the regular operators that are executed on an element by element basis ( such as +、-、、/、//、*), There's also a way to compute the product of matrices @ Operator :
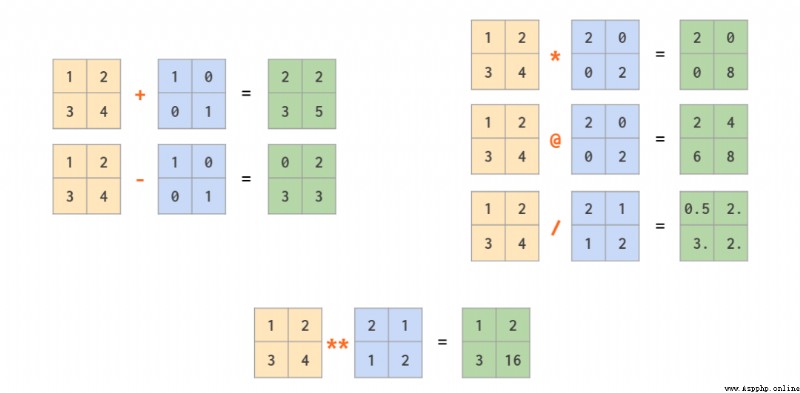
We've covered scalar to array broadcasting in the first part , After generalization based on it ,NumPy Mixed operation of support vector and matrix , Even the operation between two vectors :
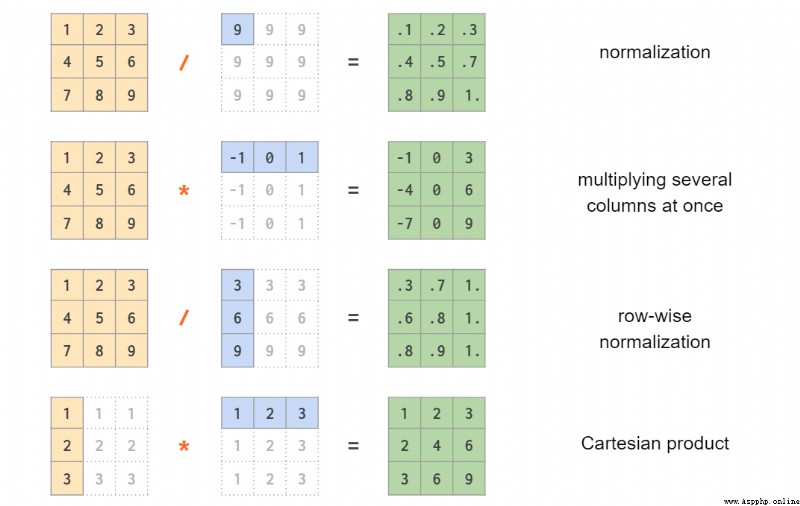
Broadcast in a two-dimensional array
Row vector and column vector
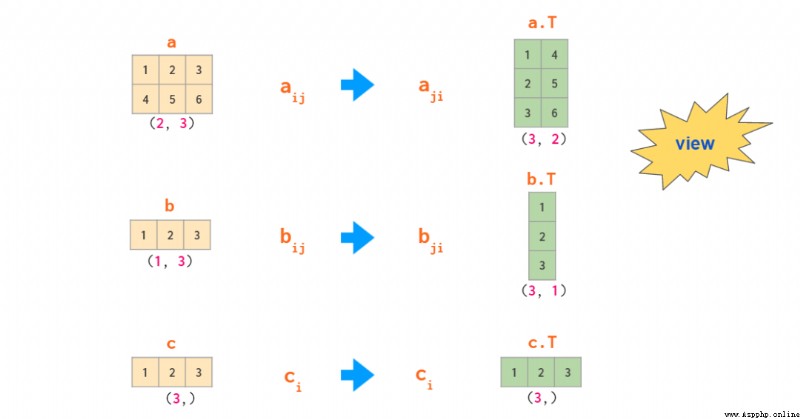
As the example above shows , In two dimensions , Row vectors and column vectors are treated differently . This is the same as having some kind of one-dimensional array NumPy Practice is different ( Like two-dimensional arrays a— Of the j Column a[:,j] It's a one-dimensional array ). By default , One dimensional arrays are treated as row vectors in two-dimensional operations , So when you multiply a matrix by a row vector , You can use shapes (n,) or (1, n)—— The result is the same . If you need a column vector , There are many ways to get it based on one-dimensional arrays , But here's the surprise 「 Transposition 」 Not one of them .
There are two operations to get two-dimensional array based on one-dimensional array : Use reshape Shape and use newaxis Index :
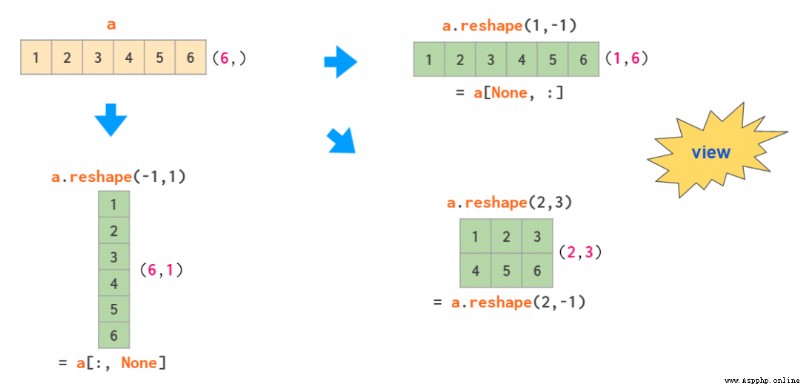
among -1 This parameter tells reshape Automatically calculate the size of one of the dimensions , In square brackets None Is used as np.newaxis Shortcut to , This will add an empty axis.
therefore ,NumPy There are three types of vectors : One dimensional vector 、 Two dimensional row vectors and two dimensional column vectors . The figure below shows how these three vectors are transformed :

One dimensional vector 、 The transformation between two-dimensional row vector and two-dimensional column vector . According to the principles of broadcasting , One dimensional arrays can be implicitly treated as two-dimensional row vectors , So there's usually no need to perform a transition between the two —— So the corresponding area is shaded .
Matrix operation
There are two main arrays of merge functions :
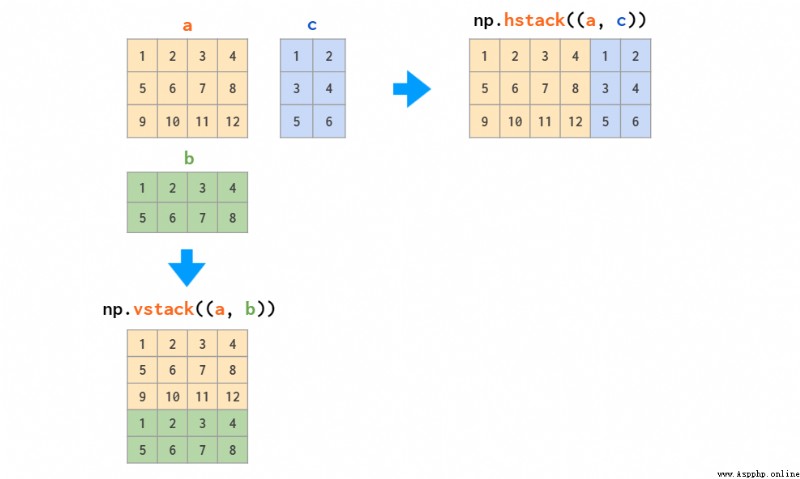
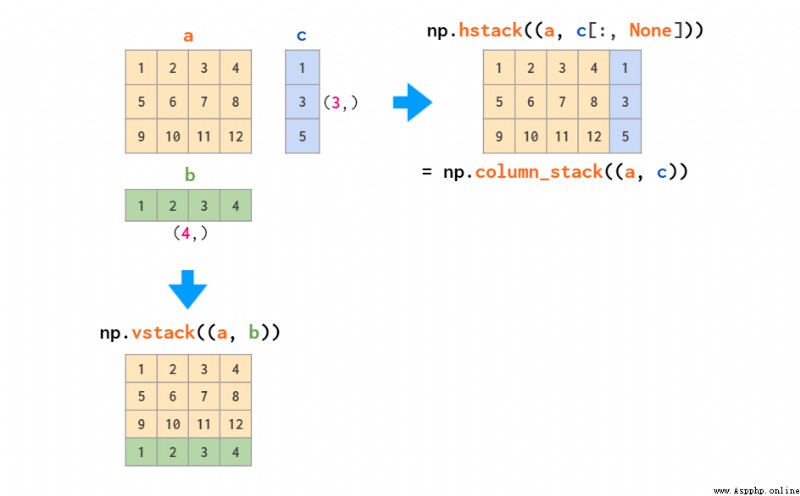
These two functions work for stacking only matrices or stacking only vectors , But when you need to stack one-dimensional arrays and matrices , Only vstack It can work :hstack There will be a dimension mismatch error , The reasons are described above , One dimensional arrays are treated as row vectors , Instead of column vectors . In response to this question , The solution is either to convert it to a row vector , Or you can do it automatically column_stack function :
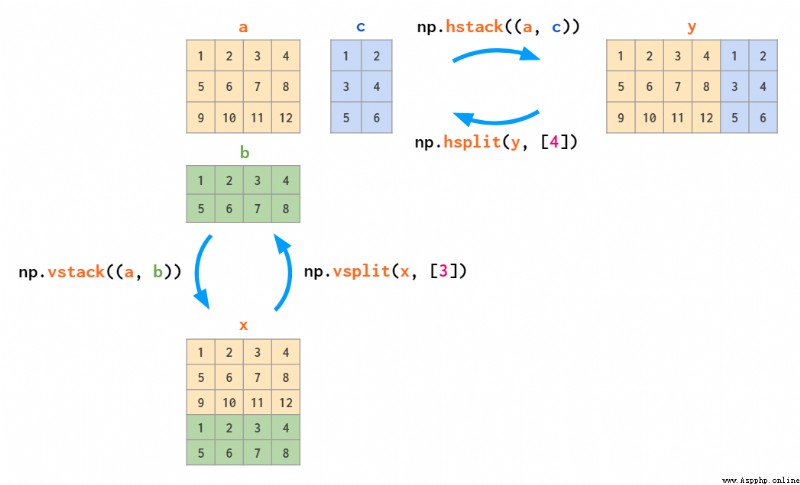
The reverse operation of stacking is splitting :
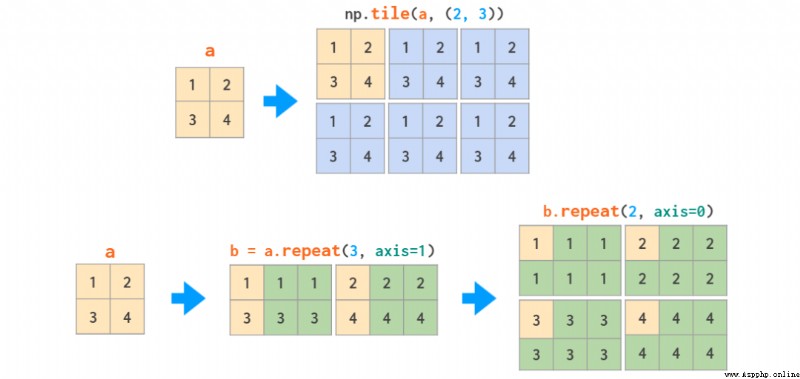
There are two ways to copy a matrix : Copy - Pasted tile And page printing repeat:
delete You can delete specific rows and columns :
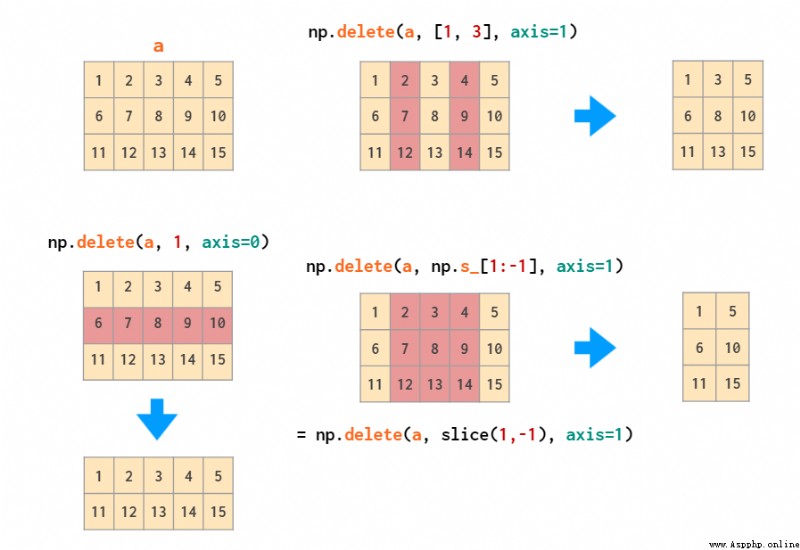
The reverse operation of deletion is used as insertion , namely insert:
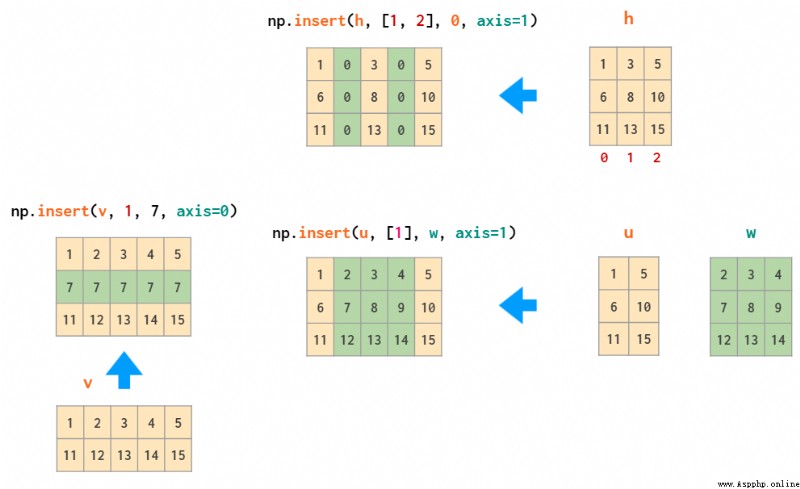
append Functions are like hstack equally , Cannot transpose one-dimensional arrays automatically , So again , Or you need to change the shape of the vector , Or you need to add a dimension , Or use column_stack:
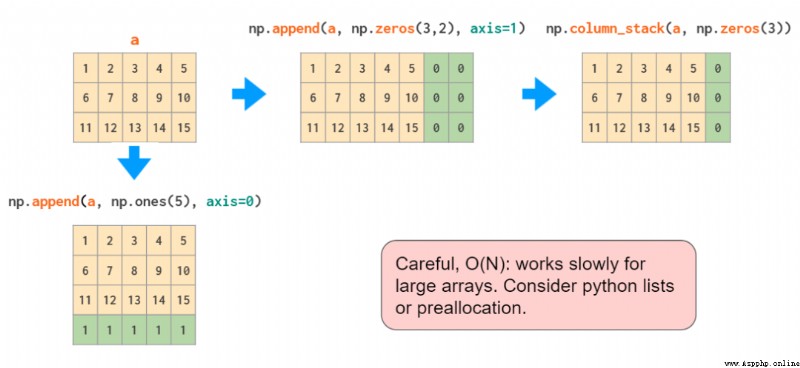
in fact , If you just need to add constant values to the edge of the array , that ( Slightly more complicated )pad Functions should be enough :
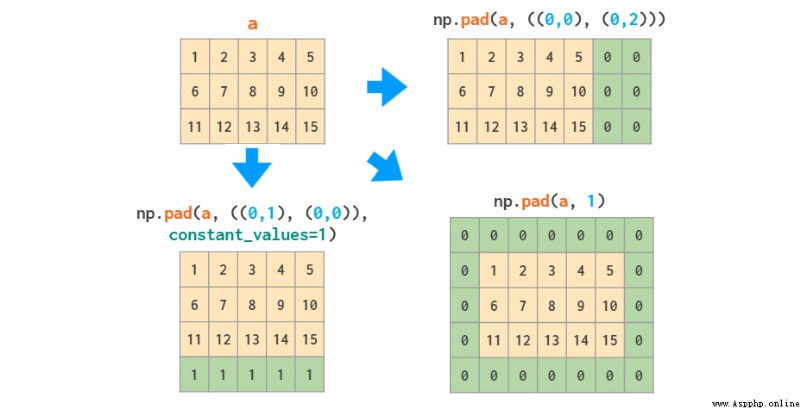
grid
Broadcast rules make it easier to manipulate the grid . Suppose you have the following matrix ( But it's very big ):

Use C And use Python Create a matrix comparison
These two methods are slow , Because they use Python loop . To solve such problems ,MATLAB The way to do this is to create a grid :
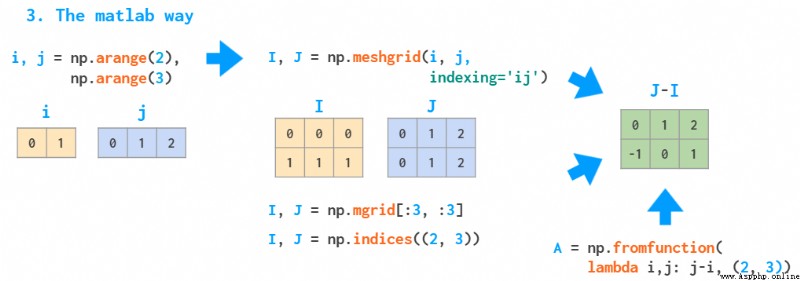
Use MATLAB Create a sketch of the grid
Use the parameters provided above I and J,meshgrid Function takes any set of indexes as input ,mgrid It's just segmentation ,indices Only full index ranges can be generated ,fromfunction The function provided is called only once .
But actually ,NumPy There's a better way to do it . We don't have to spend all our memory on I and J On the matrix . It's enough to store vectors of the right shape , Broadcasting rules can do the rest of the work .

Use NumPy Create a sketch of the grid
No, indexing=’ij’ Parameters ,meshgrid Will change the order of these parameters :J, I= np.meshgrid(j, i)—— This is a kind of xy Pattern , To visualize 3D Charts are useful .
Get matrix Statistics
and sum equally ,min、max、argmin、argmax、mean、std、var And all other statistical functions support axis Parameters and can be used to complete statistical calculation :
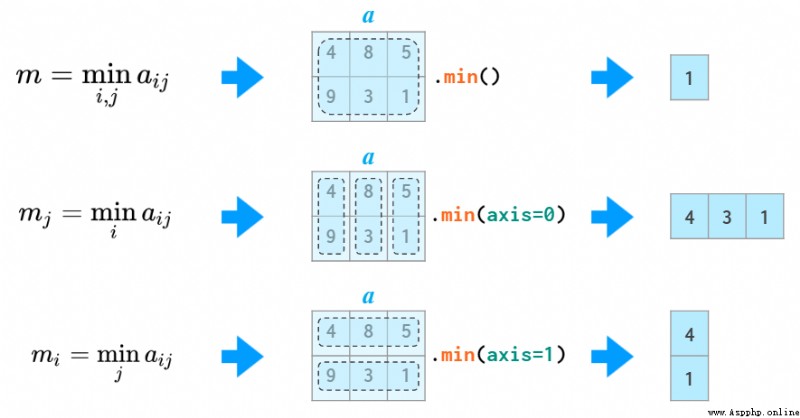
Three examples of statistical functions , In order to avoid and Python Of min Conflict ,NumPy The corresponding function in is called np.amin.
For two-dimensional and higher dimensional argmin and argmax The function returns the first instance of the minimum and maximum values , There's a bit of trouble returning the expanded index . In order to convert it into two coordinates , Need to use unravel_index function :
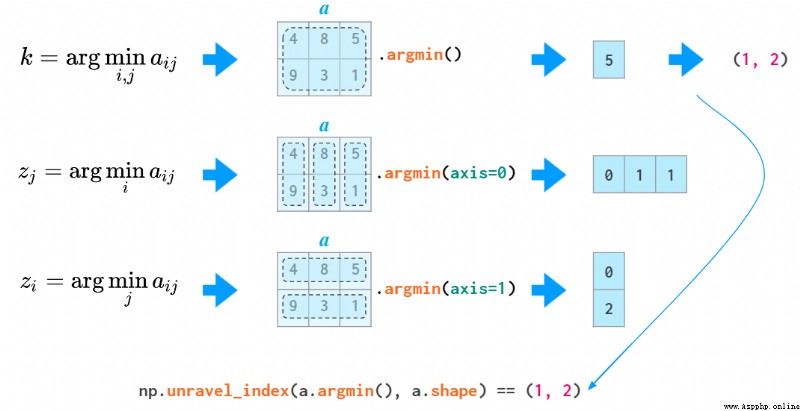
Use unravel_index Example of a function
all and any Functions also support axis Parameters :
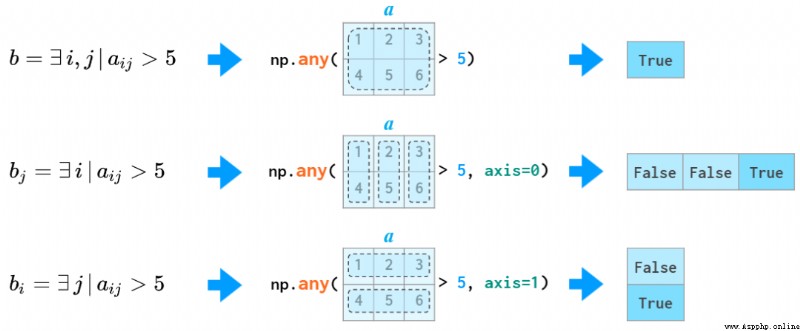
Use all and any Example of a function
Matrix ordering
axis Parameters are useful for the functions listed above , But it's useless for sorting :

Use Python List and NumPy Arrays perform sort comparisons
This is usually not the result you want to see when sorting a matrix or spreadsheet :axis There is no substitute for key Parameters . But fortunately ,NumPy Provides some auxiliary functions to support sorting by column —— Or sort by multiple columns if necessary :
1. a[a[:,0].argsort()] You can sort the array by the first column :
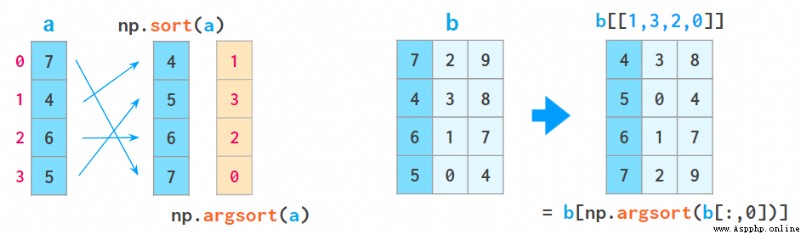
here argsort Will return the sorted index of the original array .
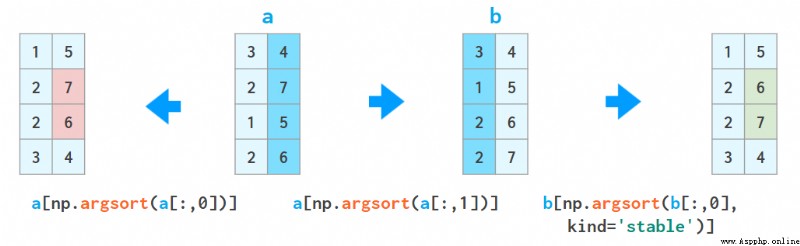
This technique can be repeated , But you have to be careful , Don't let the next sort disturb the result of the previous sort :
a = a[a[:,2].argsort()]
a = a[a[:,1].argsort(kind='stable')]
a = a[a[:,0].argsort(kind='stable')]
2. lexsort Function can sort all columns in the same way , But it's always on line , And the order of the rows to be sorted is reversed ( From the bottom up ), So it's a bit unnatural to use it , such as
- a[np.lexsort(np.flipud(a[2,5].T))] First of all, according to article 2 Column sorting , then ( When the first 2 When the values of the columns are equal ) And then according to 5 Column sorting .
– a[np.lexsort(np.flipud(a.T))] Will sort from left to right according to all columns .
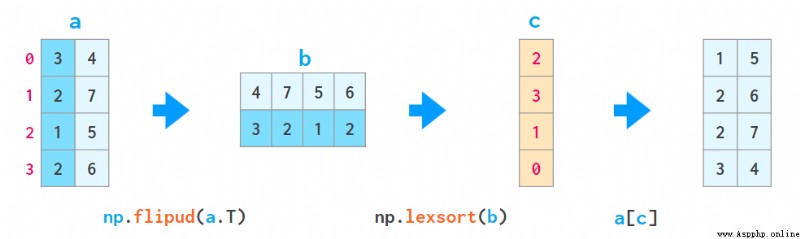
here ,flipud The matrix is flipped up and down ( To be exact axis=0 Direction , And a[::-1,...] equally , Three of the dots represent 「 All the other dimensions 」, So flipping this one-dimensional array is all of a sudden flipud, instead of fliplr.
3. sort One more order Parameters , But if it's normal at first ( Unstructured ) Array , It's not fast to execute , It's not easy to use .
4. stay pandas It's probably a better choice to execute it in , Because in pandas in , This particular operation is much more readable , It's not so easy to make mistakes :
– pd.DataFrame(a).sort_values(by=[2,5]).to_numpy() I'll start with 2 Column sorting , And then according to section 5 Column sorting .
– pd.DataFrame(a).sort_values().to_numpy() Will sort from left to right according to all columns .
Three dimensions and higher
When you adjust the shape of a one-dimensional vector or transform nested vectors Python List to create 3D Array time , The meaning of index is (z,y,x). The first index is the number of planes , And then there are the coordinates on that plane :
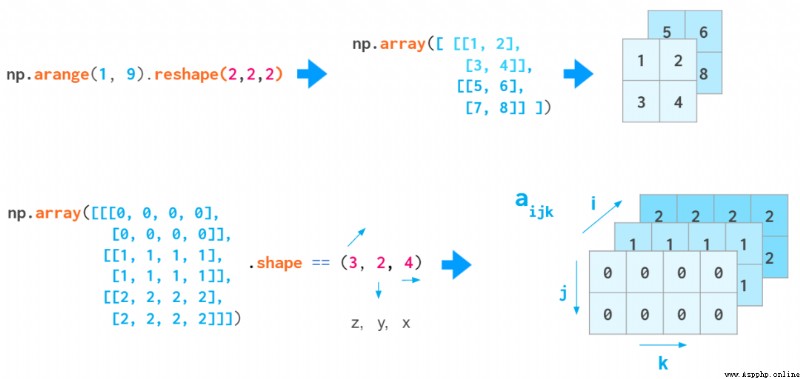
Exhibition (z,y,x) A schematic diagram of the sequence
This index order is very convenient , for instance , It can be used to save some grayscale images :a[i] It's index number i A shortcut to an image .
But this index order is not universal . When operating RGB In the picture , You usually use (y,x,z) The order : First, two pixel coordinates , The last one is the color coordinates (Matplotlib Medium is RGB,OpenCV Medium is BGR):
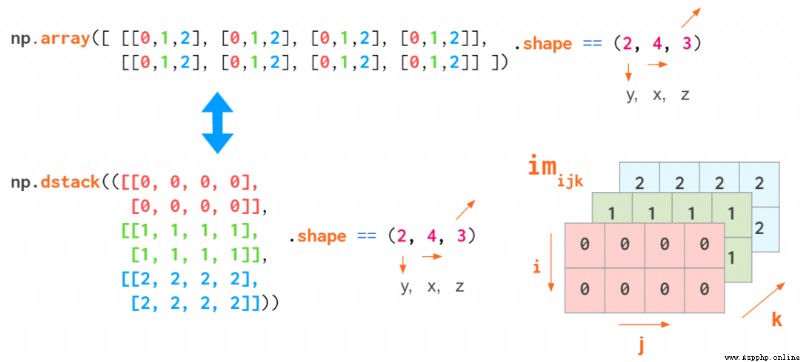
Exhibition (y,x,z) A schematic diagram of the sequence
such , We can easily index specific pixels :a[i,j] Can provide (i,j) Positional RGB Tuples .
therefore , The actual command to create the geometry depends on the conventions in your field :
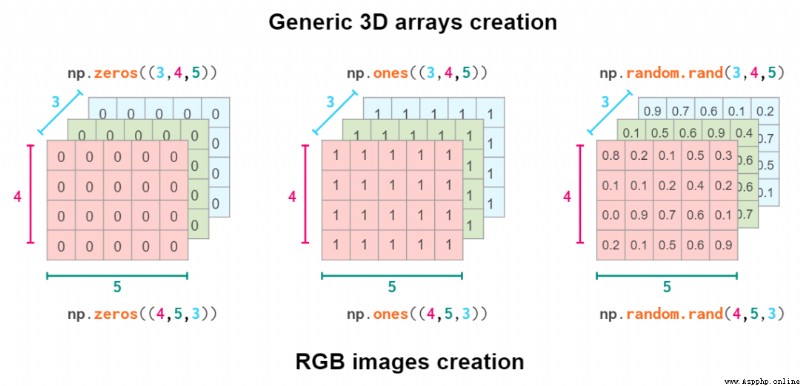
Create general 3D arrays and RGB Images
Obviously ,hstack、vstack、dstack These functions don't support these conventions . They're hard coded (y,x,z) Index order of , namely RGB The order of the images :
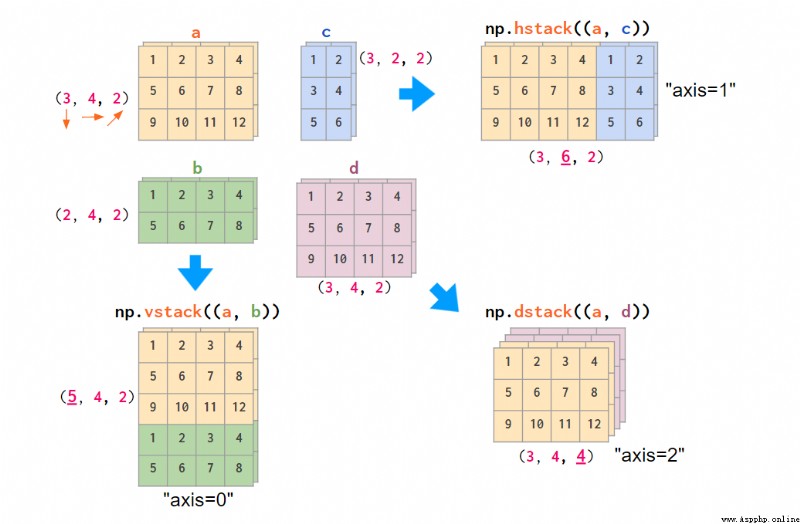
NumPy Use (y,x,z) A schematic diagram of the sequence , The stack RGB Images ( There are only two colors here )
If your data layout is different , Use concatenate It's more convenient to stack images with the command , To one axis Parameter enter a clear index value :
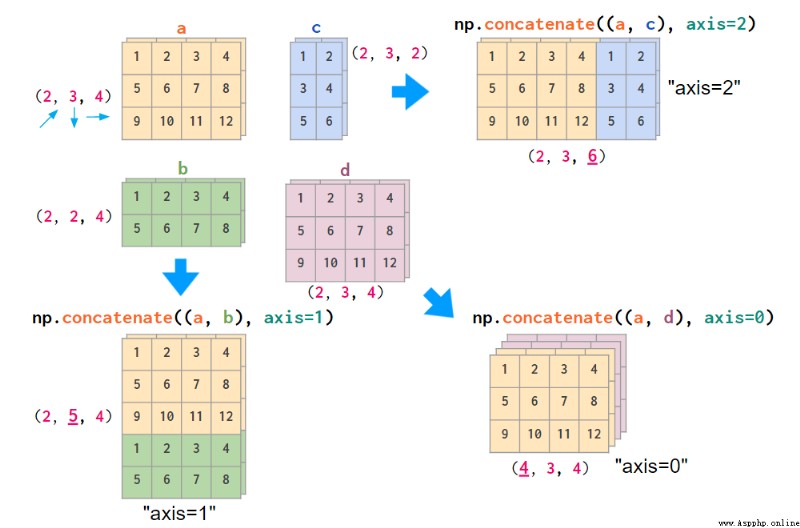
Stack general 3D arrays
If you're not used to thinking axis Count , You can convert the array to hstack And so on :

Convert an array to hstack In the form of hard coded schematic diagram
The cost of this conversion is very low : No actual replication is performed , It's just the order of the mixed indexes during execution .
Another operation that can mix index order is array transpose . Understanding it may make you more familiar with 3D arrays . According to what you decide to use axis The order is different , The actual command to transpose all planes of the array will be different : For general arrays , It exchanges indexes 1 and 2, Yes RGB The image is 0 and 1:
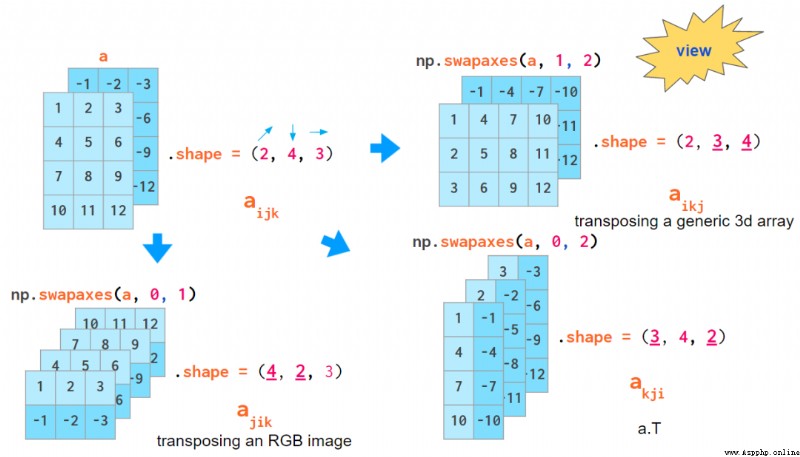
The command to transpose all planes of a 3D data
But here's the interesting thing ,transpose Default axes Parameters ( And the only a.T Operation mode ) Will rotate the direction of the index order , This is not consistent with the above two index order conventions .
Last , There is also a function that prevents you from using too much training when dealing with multidimensional arrays , It also makes your code simpler ——einsum( Einstein's summation ):

It sums the array along the repeated index . In this particular case ,np.tensordot(a, b, axis=1) Enough to deal with both , But in more complex cases ,einsum It could be faster , And it's usually easier to read and write —— As long as you understand the logic behind it .
If you want to test your NumPy Skill ,GitHub Yes 100 A rather difficult exercise :https://github.com/rougier/numpy-100.
Your favorite NumPy What is the function ? Please share with us !
Link to the original text :https://medium.com/better-programming/numpy-illustrated-the-visual-guide-to-numpy-3b1d4976de1d
Past highlights
It is suitable for beginners to download the route and materials of artificial intelligence ( Image & Text + video ) Introduction to machine learning series download Chinese University Courses 《 machine learning 》( Huang haiguang keynote speaker ) Print materials such as machine learning and in-depth learning notes 《 Statistical learning method 》 Code reproduction album machine learning communication qq Group 955171419, Please scan the code to join wechat group 