Reference blog , I also read this article to get started .
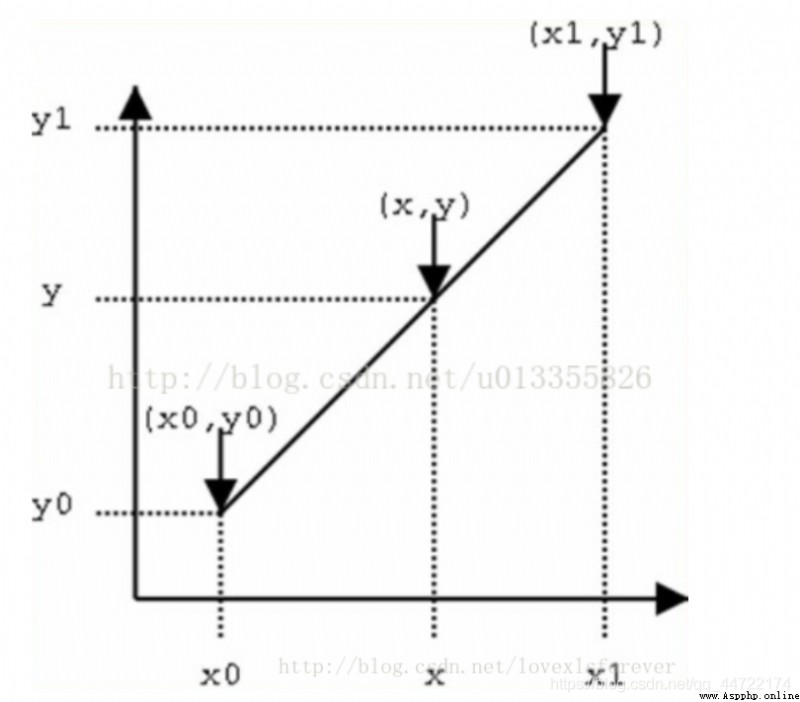
The simple linear interpolation is just like the expression of the function obtained by the two-point method in junior high school , utilize y0 and y1 Weighted representation of y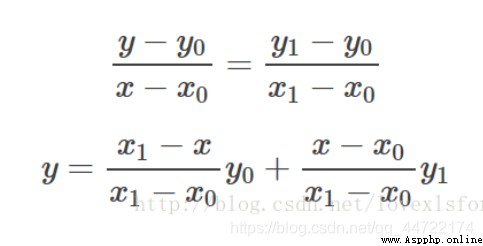
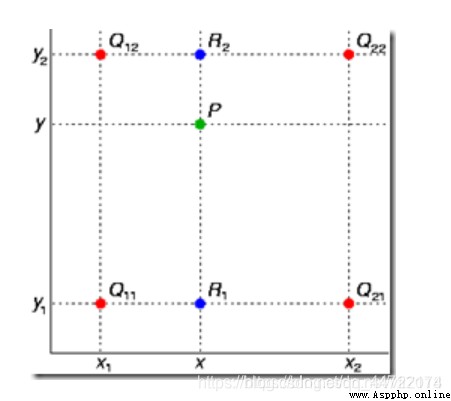
Interpolate from two directions respectively :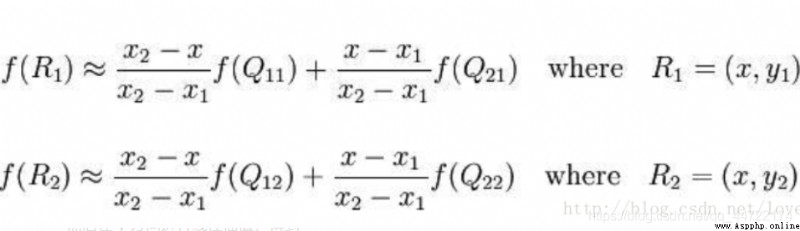
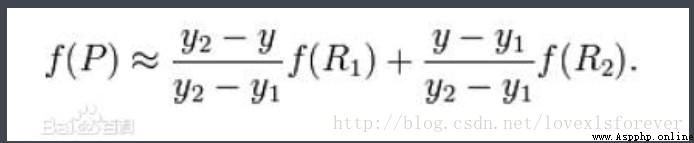
Merge the above formula :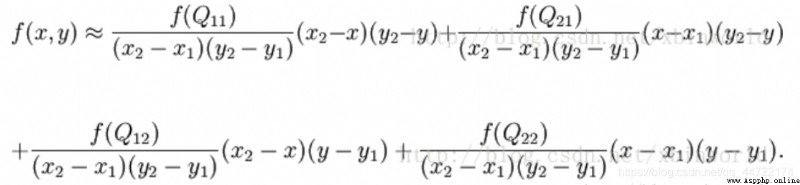
Double line interpolation algorithm is a better image scaling algorithm , It makes full use of the four real pixel values around the virtual points in the source image to jointly determine a pixel value in the target image , Therefore, the scaling effect is much better than simple nearest neighbor interpolation . Because image bilinear interpolation only uses adjacent 4 A little bit , Therefore, the denominator of the following formula is 1. Algorithm description : For a destination pixel , Set the floating-point coordinates obtained by inverse transformation to (i+u,j+v) ( among i、j Are integer parts of floating-point coordinates ,u、v Is the decimal part of the floating-point coordinates , It's a value [0,1) Floating point numbers in intervals ), Then the value of this pixel f(i+u,j+v) The coordinates in the original image can be (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1) The corresponding values of the surrounding four pixels determine , namely :
f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)
among f(i,j) Represents the source image (i,j) Pixel value at , And so on . Single linear interpolation : Known data (x0, y0) And (x1, y1), To calculate [x0, x1] Somewhere in the interval x On a straight line y value . Bilinear interpolation : Known functions f stay Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) as well as Q22 = (x2, y2) The value of four points . Find unknown function f At point P = (x, y) Value .
from PIL import Image
from datetime import datetime
import matplotlib.pyplot as plt
import numpy as np
import math
import os
img_path = r'D:\jupyter_py\in50.jpg' # The address of the source graph
target_size = (600,800, 3) # The size of the target image
img_arr = np.array(Image.open(img_path), np.uint8)
source_img = Image.fromarray(img_arr.astype(np.uint8)) # Source image coding
plt.imshow(source_img)
plt.show()
source_size = img_arr.shape # Source image size
print(source_size)
ratio_x, ratio_y = source_size[0]/target_size[0], source_size[1]/target_size[1] # Length width ratio of source image to target image
def cal(x, y, c): # What is passed in is the coordinate value from the target image to the original image , But it's not an integer
x, y = math.modf(x), math.modf(y) # Get the integer and decimal parts of the input value
mod_x, int_x, mod_y, int_y = round(x[0],4),int(x[1]),round(y[0],4),int(y[1]) # The decimal part is reserved 4 position , Index must be an integer
#print(int_x, int_y)
if int_x<source_size[0]-1 and int_y<source_size[1]-1: # If this condition is not added , The index value will overflow
p1 = (1-mod_x)*(1-mod_y)*img_arr[int_x, int_y, c] + mod_x*(1-mod_y)*img_arr[int_x+1, int_y, c]
p2 = (1-mod_x)*mod_y*img_arr[int_x, int_y+1, c] + mod_x*mod_y*img_arr[int_x+1, int_y+1, c]
else:
p1 = (1-mod_x)*(1-mod_y)*img_arr[int_x, int_y, c] + mod_x*(1-mod_y)*img_arr[int_x, int_y, c]
p2 = (1-mod_x)*mod_y*img_arr[int_x, int_y, c] + mod_x*mod_y*img_arr[int_x, int_y, c]
p = p1 + p2 # The principle formula
return p # The above treatment is hasty ,x,y Three times of condition judgment shall be strictly conducted for each overflow
if __name__ == '__main__':
start = datetime.now() # Calculate the operation time
resized_img = [cal(i*ratio_x, j*ratio_y, c) for i in range(target_size[0]) for j in range(target_size[1]) for c in range(target_size[2])] # Calculate from three dimensions
resized_img = np.array(resized_img).reshape((target_size[0], target_size[1], target_size[2]))
end = datetime.now()
seconds = (end-start).seconds
print('process cost {}s'.format(seconds)) # Output calculation time
resized_show = Image.fromarray(resized_img.astype(np.uint8))
resized_show.save(r"./1.jpg") # Save the target image
plt.imshow(resized_show) # Display the target image
plt.show()

