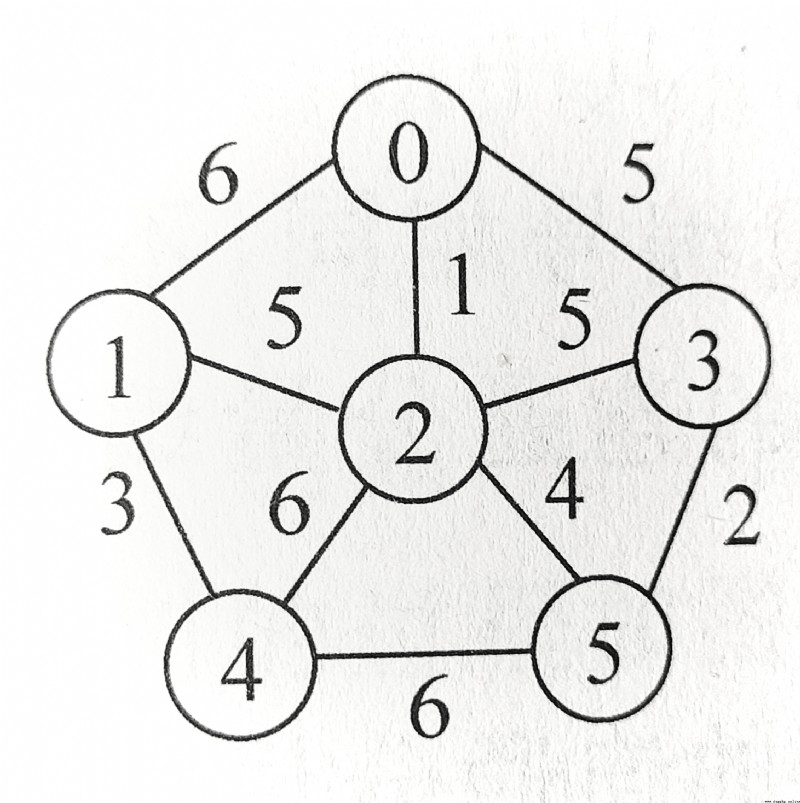
Use the following code to create
import copyfrom typing import ListMAXV = 10 # Maximum number of vertices INF = 0x3f3f3f3f # ( Hexadecimal ) Express ∞# Design adjacency matrix class class MatGraph: def __init__(self, n=0, e=0): self.edges = [] self.vexs = [] self.n = n self.e = edef CreateMatGraph(self,a,n,e): # Create an adjacency matrix self.n = n # Number of vertices n self.e = e # Number of edges e self.edges = copy.deepcopy(a) # Deep copy to adjacency matrix adef DisMatGraph(self): # Adjacency matrix of output graph for i in range(self.n): for j in range(self.n): if self.edges[i][j] == INF: print("%4s"%("∞"),end='') else: print("%5d"%(self.edges[i][j]),end='') print()# Prim The algorithm constructs the minimum spanning tree def Prim(g,v): global min, k lowcost = [0]*MAXV # Build array : Minimum weight closest = [0]*MAXV # Build array : Some recent for i in range(g.n): # to lowcost[] and closest[] Set the initial value ,i Is the number of a vertex lowcost[i] = g.edges[v][i] # lowcost[] Record the weight of the edge closest[i] = v # closest[] Record the nearest vertex for i in range(1,g.n): # Find all the edges of the minimum spanning tree min = INF # use INF Not connected ( The weight is infinite ) k = -1 # use -1 Indicates that the edge does not exist for j in range(g.n): # Find out the distance from ( Pick vertex set )U Nearest vertex k if lowcost[j] != 0 and lowcost[j]<min: # If the weight of the selected edge is less than the value in the corresponding vertex list min = lowcost[j] # Then update the array ( Shortest path ) The value is the weight of the edge k = j # k Record the number of the smallest vertex print("(%d,%d):%d"%(closest[k],k,+min),end='') # Output the edges of the minimum spanning tree lowcost[k] = 0 # to update lowcost Array to record changes for j in range(g.n): # Find the minimum distance array if lowcost[j] != 0 and g.edges[k][j] < lowcost[j]: # Determine the minimum weight lowcost[j] = g.edges[k][j] # modify lowcost closest[j] = k # modify closestif __name__ == '__main__':
