什麼是相機標定?
隨著科技和經濟的蓬勃發展,機器人作業、汽車自動導航等技術已經得到廣泛應用,在很大程度上推動了社會生產力的發展。不論是主動光學視覺傳感或者是被動光學視覺傳感,要從圖像推知物空間的三維信息,或反之,從空間三維信息推知二維圖像坐標,都必須確定相機在參考坐標系中的空間位置和取向,以及相機本身的幾何和光學參數為解決這個問題所需用到相機標定技術
相機標定的作用在於消除由於相機產生的圖像畸變,從而校正圖像,為處理計算出精確數值提供可能。
由此,相機標定成了系統准確的先決條件。
從真實的三維世界坐標,可以得到二維的相機坐標,
但是我們從二維的相機坐標,能否准確的推算出真實的三維世界的坐標呢?這就是相機標定的意義。
相機標定的原理是什麼?
相機標定指建立相機圖像像素位置與場景點位置之間的關系,根據相機成像模型,由特征點在圖像中坐標與世界坐標的對應關系,求解相機模型的參數。相機需要標定的模型參數包括內部參數和外部參數。
針孔相機成像原理其實就是利用投影將真實的三維世界坐標轉換到二維的相機坐標上去,其模型示意圖如下圖所示: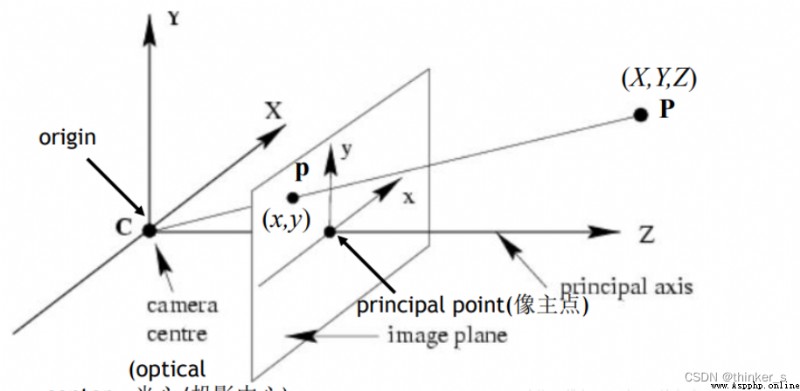
從圖中我們可以看出,在世界坐標中的一條直線上的點在相機上只呈現出了一個點,其中發生了非常大的變化,同時也損失和很多重要的信息,這正是我們3D重建、目標檢測與識別領域的重點和難點。實際中,鏡頭並非理想的透視成像,帶有不同程度的畸變。理論上鏡頭的畸變包括徑向畸變和切向畸變,切向畸變影響較小,通常只考慮徑向畸變。
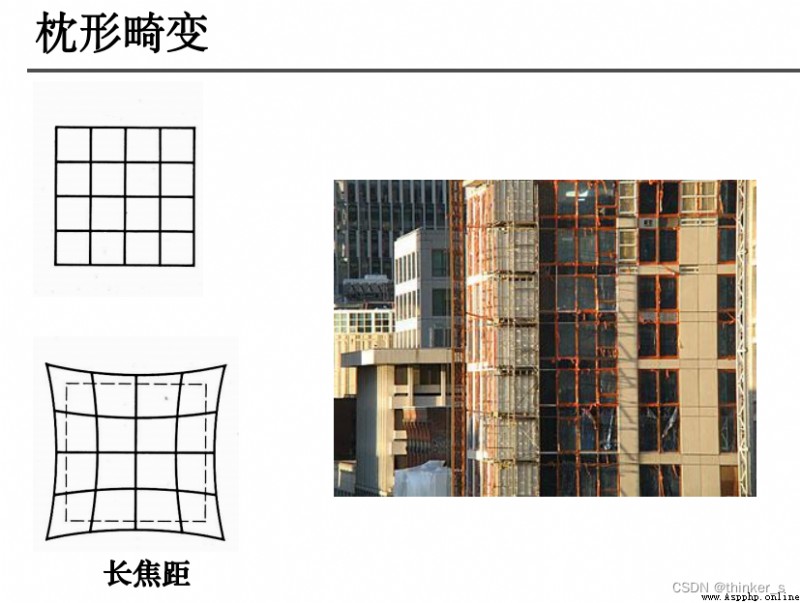
徑向畸變:
徑向畸變主要由鏡頭徑向曲率產生(光線在遠離透鏡中心的地方比靠近中心的地方更加彎曲)。導致真實成像點向內或向外偏離理想成像點。其中畸變像點相對於理想像點沿徑向向外偏移,遠離中心的,稱為枕形畸變;徑向畸點相對於理想點沿徑向向中心靠攏,稱為桶狀畸變。
# -*- codeing =utf-8 -*-
import cv2
import numpy as np
import glob
# 找棋盤格角點
# 阈值
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
#棋盤格模板規格
w = 11 #內角點個數,內角點是和其他格子連著的點
h = 8
# 世界坐標系中的棋盤格點,例如(0,0,0), (1,0,0), (2,0,0) ....,(8,5,0),去掉Z坐標,記為二維矩陣
objp = np.zeros((w*h,3), np.float32)
objp[:,:2] = np.mgrid[0:w,0:h].T.reshape(-1,2)
# 儲存棋盤格角點的世界坐標和圖像坐標對
objpoints = [] # 在世界坐標系中的三維點
imgpoints = [] # 在圖像平面的二維點
images = glob.glob('./ima/*.jpg') # 標定所用圖像
for fname in images:
img = cv2.imread(fname)
img = cv2.resize(img, (700, 375), interpolation=cv2.INTER_AREA)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# 找到棋盤格角點
# 棋盤圖像(8位灰度或彩色圖像) 棋盤尺寸 存放角點的位置
ret, corners = cv2.findChessboardCorners(gray, (w,h),None)
# 如果找到足夠點對,將其存儲起來
if ret == True:
# 角點精確檢測
# 輸入圖像 角點初始坐標 搜索窗口為2*winsize+1 死區 求角點的迭代終止條件
cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
objpoints.append(objp)
imgpoints.append(corners)
# 將角點在圖像上顯示
cv2.drawChessboardCorners(img, (w,h), corners, ret)
cv2.imshow('findCorners',img)
cv2.waitKey(1000)
cv2.destroyAllWindows()
#標定、去畸變
# 輸入:世界坐標系裡的位置 像素坐標 圖像的像素尺寸大小 3*3矩陣,相機內參數矩陣 畸變矩陣
# 輸出:標定結果 相機的內參數矩陣 畸變系數 旋轉矩陣 平移向量
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
# mtx:內參數矩陣
# dist:畸變系數
# rvecs:旋轉向量 (外參數)
# tvecs :平移向量 (外參數)
print (("ret:"),ret)
print (("mtx:\n"),mtx) # 內參數矩陣
print (("dist:\n"),dist) # 畸變系數 distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print (("rvecs:\n"),rvecs) # 旋轉向量 # 外參數
print (("tvecs:\n"),tvecs) # 平移向量 # 外參數
# 去畸變
img2 = cv2.imread('./ima/2.jpg')
h,w = img2.shape[:2]
# 我們已經得到了相機內參和畸變系數,在將圖像去畸變之前,
# 我們還可以使用cv.getOptimalNewCameraMatrix()優化內參數和畸變系數,
# 通過設定自由自由比例因子alpha。當alpha設為0的時候,
# 將會返回一個剪裁過的將去畸變後不想要的像素去掉的內參數和畸變系數;
# 當alpha設為1的時候,將會返回一個包含額外黑色像素點的內參數和畸變系數,並返回一個ROI用於將其剪裁掉
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),0,(w,h)) # 自由比例參數
dst = cv2.undistort(img2, mtx, dist, None, newcameramtx)
# 根據前面ROI區域裁剪圖片
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('./ima/calibresult.jpg',dst)
# 反投影誤差
# 通過反投影誤差,我們可以來評估結果的好壞。越接近0,說明結果越理想。
# 通過之前計算的內參數矩陣、畸變系數、旋轉矩陣和平移向量,使用cv2.projectPoints()計算三維點到二維圖像的投影,
# 然後計算反投影得到的點與圖像上檢測到的點的誤差,最後計算一個對於所有標定圖像的平均誤差,這個值就是反投影誤差。
total_error = 0
for i in range(len(objpoints)):
imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
total_error += error
print (("total error: "), total_error/len(objpoints))
輸入圖片樣例:

輸出:

輸出參數:
ret: 3.2089084482428625
mtx:
[[298.22403646 0. 349.40224378]
[ 0. 249.9301803 308.87597705]
[ 0. 0. 1. ]]
dist:
[[-0.01542965 -0.05742923 0.04474822 0.0136368 0.01877975]]
rvecs:
[array([[-0.30947814],
[ 0.33401078],
[ 2.41641327]]), array([[-0.11406369],
[-0.03094208],
[ 1.12212397]]), array([[-0.09734436],
[-0.01784972],
[ 1.48696195]]), array([[-0.2939506 ],
[ 0.50513446],
[ 3.02645373]]), array([[0.09769781],
[0.37093298],
[3.07432249]]), array([[-0.14125134],
[-0.40375224],
[-1.67651102]]), array([[-0.15323876],
[-0.37674176],
[-1.65194111]]), array([[-0.065466 ],
[-0.36197005],
[-1.95960452]]), array([[ 0.13847532],
[-0.1150688 ],
[-2.01085342]]), array([[-0.17608388],
[-0.32411952],
[-1.32817709]]), array([[-0.20703879],
[ 0.00763589],
[ 0.28986026]])]
tvecs:
[array([[ 8.9229434 ],
[-8.32737698],
[16.89551684]]), array([[ 0.87209331],
[-15.33212787],
[ 13.59312779]]), array([[ 3.59921773],
[-14.90849088],
[ 13.571556 ]]), array([[ 4.8131481 ],
[-2.24922584],
[14.75699795]]), array([[ 3.22211236],
[-1.80439912],
[13.44002642]]), array([[-2.34496458],
[-2.33449517],
[12.09128798]]), array([[-2.22919308],
[-2.35073525],
[12.0281442 ]]), array([[-2.13702847],
[-2.76957196],
[12.54089188]]), array([[-1.05509505],
[-5.39874714],
[12.34265496]]), array([[-1.72209533],
[-2.87686218],
[13.2875987 ]]), array([[ -4.15293414],
[-12.73524946],
[ 14.8851007 ]])]
total error: 0.3381936202146006