What is camera calibration ?
With the vigorous development of science and technology and economy , Robot work 、 Auto navigation and other technologies have been widely used , To a great extent, it has promoted the development of social productive forces . Whether it is active optical vision sensing or passive optical vision sensing , To infer the three-dimensional information of object space from the image , Or vice versa , Deduce two-dimensional image coordinates from three-dimensional spatial information , The spatial position and orientation of the camera in the reference coordinate system must be determined , And the geometric and optical parameters of the camera itself. Camera calibration technology is needed to solve this problem
The function of camera calibration is to eliminate the image distortion caused by the camera , Thus, the image is corrected , It provides the possibility for processing and calculating accurate values .
thus , Camera calibration has become a prerequisite for the accuracy of the system .
From the real three-dimensional world coordinates , You can get two-dimensional camera coordinates ,
But we start with two-dimensional camera coordinates , Can we accurately calculate the coordinates of the real three-dimensional world ? This is the meaning of camera calibration .
What is the principle of camera calibration ?
Camera calibration refers to establishing the relationship between camera image pixel position and scene point position , According to the camera imaging model , The correspondence between the coordinates of feature points in the image and the world coordinates , Solve the parameters of the camera model . The model parameters to be calibrated include internal parameters and external parameters .
The imaging principle of pinhole camera is to convert the real three-dimensional world coordinates to two-dimensional camera coordinates by projection , The model diagram is shown in the figure below :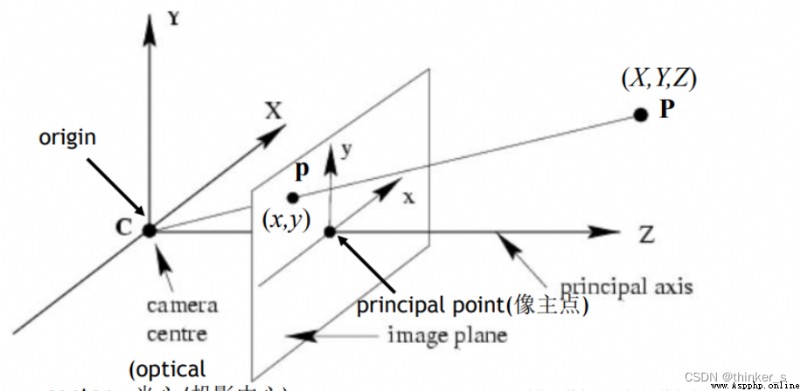
As we can see from the picture , A point on a straight line in world coordinates shows only one point on the camera , Great changes have taken place , At the same time, it also loses and a lot of important information , This is exactly what we 3D The reconstruction 、 Key points and difficulties in the field of target detection and recognition . In the actual , The lens is not ideal for perspective imaging , With varying degrees of distortion . Theoretically, lens distortion includes radial distortion and tangential distortion , Tangential distortion has little effect , Usually only radial distortion is considered .
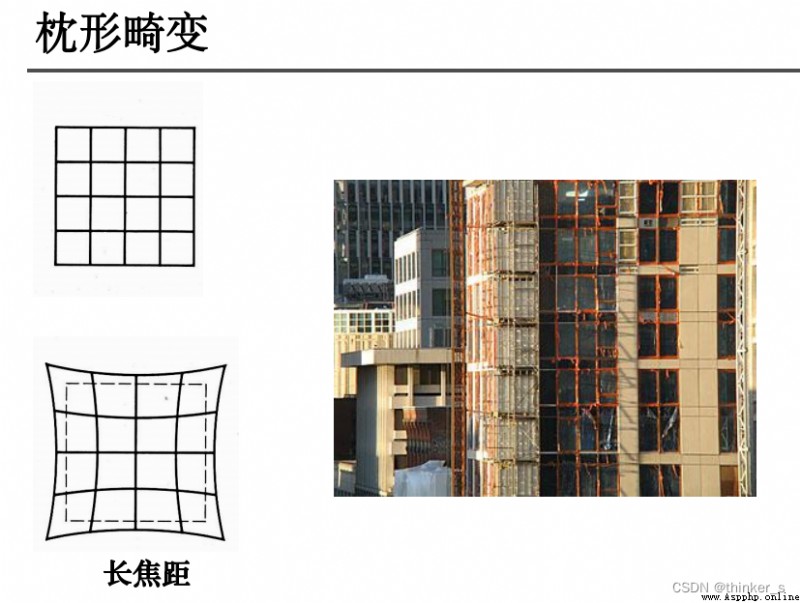
Radial distortion :
Radial distortion is mainly caused by the radial curvature of the lens ( The light is more curved away from the center of the lens than near the center ). Cause the real imaging point to deviate inward or outward from the ideal imaging point . The distorted image point is offset radially outward relative to the ideal image point , Far from the center , It's called occipital distortion ; The radial abnormal point is close to the center along the radial direction relative to the ideal point , Called barrel distortion .
# -*- codeing =utf-8 -*-
import cv2
import numpy as np
import glob
# Find the corner of the chessboard
# threshold
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# Checkerboard template specification
w = 11 # Number of inner corners , The inner corner is the point connected with other grids
h = 8
# Checkerboard grid points in the world coordinate system , for example (0,0,0), (1,0,0), (2,0,0) ....,(8,5,0), Get rid of Z coordinate , Write it down as a two-dimensional matrix
objp = np.zeros((w*h,3), np.float32)
objp[:,:2] = np.mgrid[0:w,0:h].T.reshape(-1,2)
# Save the world coordinate and image coordinate pair of checkerboard corner points
objpoints = [] # Three dimensional points in the world coordinate system
imgpoints = [] # Two dimensional points in the image plane
images = glob.glob('./ima/*.jpg') # Image used for calibration
for fname in images:
img = cv2.imread(fname)
img = cv2.resize(img, (700, 375), interpolation=cv2.INTER_AREA)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# Find the corner of the chessboard
# Chessboard image (8 Bit grayscale or color image ) Chessboard size Where to store the corners
ret, corners = cv2.findChessboardCorners(gray, (w,h),None)
# If you find enough right , Store it
if ret == True:
# Accurate corner detection
# The input image Initial coordinates of corner points The search window is 2*winsize+1 dead zone Find the iterative termination condition of the corner
cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
objpoints.append(objp)
imgpoints.append(corners)
# Show corners on image
cv2.drawChessboardCorners(img, (w,h), corners, ret)
cv2.imshow('findCorners',img)
cv2.waitKey(1000)
cv2.destroyAllWindows()
# calibration 、 To distort
# Input : Position in the world coordinate system Pixel coordinates The pixel size of the image 3*3 matrix , Camera intrinsic parameter matrix Distortion matrix
# Output : Calibration results The internal parameter matrix of the camera Distortion coefficient Rotation matrix Translation vector
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
# mtx: Internal parameter matrix
# dist: Distortion coefficient
# rvecs: Rotating vector ( External parameters )
# tvecs : Translation vector ( External parameters )
print (("ret:"),ret)
print (("mtx:\n"),mtx) # Internal parameter matrix
print (("dist:\n"),dist) # Distortion coefficient distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print (("rvecs:\n"),rvecs) # Rotating vector # External parameters
print (("tvecs:\n"),tvecs) # Translation vector # External parameters
# To distort
img2 = cv2.imread('./ima/2.jpg')
h,w = img2.shape[:2]
# We've got intrinsic distortion coefficient of the camera , Before de distorting the image ,
# We can also use cv.getOptimalNewCameraMatrix() Optimize internal parameters and distortion coefficient ,
# By setting the free scale factor alpha. When alpha Set to 0 When ,
# It will return a clipped internal parameter and distortion coefficient that will remove the unwanted pixels after de distortion ;
# When alpha Set to 1 When , An inner parameter and distortion coefficient containing additional black pixels will be returned , And return a ROI Used to cut it out
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),0,(w,h)) # Free scale parameter
dst = cv2.undistort(img2, mtx, dist, None, newcameramtx)
# According to the front ROI Region crop picture
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('./ima/calibresult.jpg',dst)
# Back projection error
# Through the back projection error , We can evaluate the results . The closer the 0, It shows that the more ideal the result is .
# Through the internal parameter matrix calculated before 、 Distortion coefficient 、 Rotation matrix and translation vector , Use cv2.projectPoints() Calculate the projection from 3D points to 2D images ,
# Then calculate the error between the point obtained by back projection and the point detected on the image , Finally, calculate an average error for all calibrated images , This value is the back projection error .
total_error = 0
for i in range(len(objpoints)):
imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
total_error += error
print (("total error: "), total_error/len(objpoints))
Input picture sample :

Output :

Output parameters :
ret: 3.2089084482428625
mtx:
[[298.22403646 0. 349.40224378]
[ 0. 249.9301803 308.87597705]
[ 0. 0. 1. ]]
dist:
[[-0.01542965 -0.05742923 0.04474822 0.0136368 0.01877975]]
rvecs:
[array([[-0.30947814],
[ 0.33401078],
[ 2.41641327]]), array([[-0.11406369],
[-0.03094208],
[ 1.12212397]]), array([[-0.09734436],
[-0.01784972],
[ 1.48696195]]), array([[-0.2939506 ],
[ 0.50513446],
[ 3.02645373]]), array([[0.09769781],
[0.37093298],
[3.07432249]]), array([[-0.14125134],
[-0.40375224],
[-1.67651102]]), array([[-0.15323876],
[-0.37674176],
[-1.65194111]]), array([[-0.065466 ],
[-0.36197005],
[-1.95960452]]), array([[ 0.13847532],
[-0.1150688 ],
[-2.01085342]]), array([[-0.17608388],
[-0.32411952],
[-1.32817709]]), array([[-0.20703879],
[ 0.00763589],
[ 0.28986026]])]
tvecs:
[array([[ 8.9229434 ],
[-8.32737698],
[16.89551684]]), array([[ 0.87209331],
[-15.33212787],
[ 13.59312779]]), array([[ 3.59921773],
[-14.90849088],
[ 13.571556 ]]), array([[ 4.8131481 ],
[-2.24922584],
[14.75699795]]), array([[ 3.22211236],
[-1.80439912],
[13.44002642]]), array([[-2.34496458],
[-2.33449517],
[12.09128798]]), array([[-2.22919308],
[-2.35073525],
[12.0281442 ]]), array([[-2.13702847],
[-2.76957196],
[12.54089188]]), array([[-1.05509505],
[-5.39874714],
[12.34265496]]), array([[-1.72209533],
[-2.87686218],
[13.2875987 ]]), array([[ -4.15293414],
[-12.73524946],
[ 14.8851007 ]])]
total error: 0.3381936202146006