Baidu explains
Blog explanation
The Mohr tree stores Hashi values
A mokol tree , Each leaf node in the tree corresponds to a hash value .
The height of the mokol tree is h, So every mokol tree can record 2**h Integrity summary values .
Every time a leaf node is updated , You need to update the hash values of all nodes on the path from the leaf node to the root .
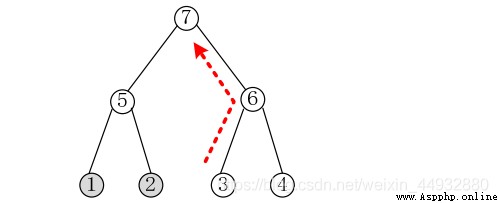
Pictured , node 1 And nodes 2 Integrity information has been stored , The new integrity information will be saved in the node 3, And because of the node 3 The value of has changed , This leads to the need to recalculate nodes 6 And nodes 7 Hash value of .
from algorithm.g_hash import G_hash
"""" l The left node r Right node p Parent node hash Stored hash value , The leaf node is updated upward every time it is modified data Other data """
class Node:
def __init__(self):
self.l=None
self.r=None
self.p=None
self.hash="\\"
self.data="\\"
def change_data(self,data):
self.data=data
self.hash=G_hash(data)
return self.hash
""" init Initialization tree root The root node h The height of the tree ,0 Represents only the root node leaf The number of leaves left add() from root Recursively add... Down h The nodes of the story height creat() establish h Tall trees ( The root node does not count ) update() It is actually adding data to the spare leaves from left to right up_update() Update the node up to know the parent node show2 Hierarchical traversal tree , Show show2 from show_tree() call sum() Is to return the number of all points of the root node """
class merkle_tree:
def __int__(self):
self.root = None
self.h=0
self.leaf=0
# add to h Nodes of the layer tree
def add(self,item,h):
l= Node()
r=Node()
l.p=item
item.l=l
r.p=item
item.r=r
h = h - 1
if h==0:
return
else:
self.add(l,h)
self.add(r,h)
# The height of the mokol tree is h, So every mokol tree can record 2h One electron
# Integrity summary value of evidence fragment .
# Except that the root node needs h layer
def creat(self,h):
self.root=Node()
self.h=h
self.leaf=2**h
self.add(self.root,h)
return self.root
# Add leaf nodes from left to right
def update(self,data,hash):
if self.leaf==0:
print(" This tree is full ")
return
temp=self.root
h=self.h
leaf=self.leaf
# For each node p,
# If the genus has more than half of its remaining leaf nodes , The next spare leaf is on the left
# p The remainder of the left node of is equal to p Subtract half of all leaf nodes from the remaining leaf nodes
# Otherwise it's on the right
# The number of leaf nodes starts from the root node and each layer is 2**(h-1)
# h=1 Is the leaf node layer
while(h!=0):
if leaf>2**(h-1):
leaf=leaf-2**(h-1)
temp=temp.l
else:
temp=temp.r
h=h-1
self.leaf-=1
temp.data=data
temp.hash=hash
self.up_update(temp)
return temp
def up_update(self,temp):
if temp.p!=None:
temp=temp.p
temp.hash=G_hash(temp.l.hash+temp.r.hash)
self.up_update(temp)
# Left to right Traverse
def show1(self,root):
if root.l!=None:
print(" towards the left ",end="")
self.show(root.l)
print(" towards the right ", end="")
self.show(root.r)
if root.l==None:
print(root.hash)
print(root.data)
# Level traversal
def show2(self,root):
x=[]
cc=[]
x.append(root)
print("\t",root.hash)
while x!=[]:
if x[0].l==None:
break
for _ in range(len(x)):
print("\t",'%-70s' % x[_].l.hash,end="")
print("\t",'%-70s' % x[_].r.hash,end="")
cc.append(x[_].l)
cc.append(x[_].r)
print("")
x=cc
cc=[]
def show_tree(self):
root=self.root
self.show2(root)
# Except for the root node
def sum(self,root):
if root.l!=None and root.r!=None:
return 2+self.sum(root.l)+self.sum(root.r)
if root.l==None or root.r ==None:
return 0
# test
b=merkle_tree()
b.creat(4)
print(b.sum(b.root))
b.update("1","1.hash")
b.update("2","2.hash")
b.update("3","3.hash")
b.show_tree()