Search for It refers to the algorithm process of finding a specific element from the element set , The search process usually returns True or False, Indicates whether the element exists .Python Through the operator in To check whether an element is in the element collection , as follows :
print("C" in ["C", "S", "D", "N"])
print("C" in (1, 2, 3))
print("c" in {
"a": "A", "b": "B", "c": "C"})
print("c" in {
1, "123", "ab"})
The operation results are as follows :
With python As an example , Because its elements have a linear or sequential relationship , Each element has a unique subscript , And the subscripts are ordered , Can be accessed sequentially , So as to carry out Sequential search . The concept of sequential search is to find elements from left to right , From the first element , If it is not found at the end of the list, it means that the element is not in the list .
The time complexity of sequential search with unordered list and sequential list is O(n), Only when there is no target element to search in the list , The efficiency of sequential search of ordered elements is higher .
The sequence search code of the unordered list is as follows :
# Order search of unordered list
def sequential_Search(alist, item): # Pass in two parameters : An unordered list with elements to search
pos = 0 # Subscript value from 0 Start
found = False
while pos < len(alist) and not found: # Until the search for elements stops
if alist[pos] == item: # If the element corresponding to the current subscript value is equal to the element to be searched ,found Variable value is True
found = True
else:
pos = pos + 1 # Subscript value plus one , Continue to search
return found
# Sequential search of an ordered list
def orderedSequential_Search(alist, item): # Pass in two parameters : A list of sequences and elements to search
pos = 0 # Subscript value from 0 Start
found = False
stop = False
while pos < len(alist) and not found and not stop:
if alist[pos] == item: # If the element corresponding to the current subscript value is equal to the element to be searched ,found The variable is equal to True
found = True
else:
if alist[pos] > item: # If the current subscript value is greater than the element to be searched , be stop The variable is equal to True
stop = True
else:
pos = pos + 1 # Subscript value plus one , Continue to search
return found
print(sequential_Search([6, 4, 5, 0], 6))
print(orderedSequential_Search([1, 2, 3, 4, 5], 6))
The operation results are as follows :
Binary search compared to sequential search , It doesn't start searching the list from the first element , But start with the middle element , So it's called Two point search . If this element is target element to search , Stop searching immediately ; If not , You can take advantage of the ordered nature of the list , Exclude half of the elements , Go down in turn , Until the target element is searched . In a nutshell , That is to divide a big problem into small problems , So as to narrow the scope , In turn, to solve .
For an ordered list , The time complexity of binary search algorithm in the worst case is O(logn), The binary search code for the ordered list is as follows :
# Binary search of ordered list
def binarySearch(alist, item): # Pass in two parameters : A list of sequences and elements to search
first = 0
last = len(alist) - 1 # The subscript value of the last element of the list
found = False
while first <= last and not found:
midpoint = (first + last) // 2 # Divide by two
if alist[midpoint] == item:
found = True
else:
if item < alist[midpoint]:
last = midpoint - 1
else:
first = midpoint + 1
return found
print(binarySearch([1, 6, 9, 10, 13, 14, 18], 14))
The operation results are as follows :
Steps to resolve :
Binary search is improved by using recursive method , The code is as follows :
# The recursive method of binary search
def binarySearch(alist, item):
if len(alist) == 0:
return False
else:
midpoint = len(alist) // 2
if alist[midpoint] == item:
return True
else:
if item < alist[midpoint]:
return binarySearch(alist[:midpoint], item) # alist[:midpoint] It means to get from the beginning to midpoint Subscript value
else:
return binarySearch(alist[midpoint + 1:], item) #alist[midpoint + 1:] It means to take from the end to midpoint+1 Subscript value
print(binarySearch([1, 6, 9, 10, 13, 14, 18], 14))
The operation results are as follows :
According to whether the contents to be sorted are in memory Sorting can be divided into inner sorting and outer sorting , Internal order The whole sorting process of is in memory , and External sorting Because there is too much to sort , Memory cannot hold , External storage is required , That is, the sorting process is included 、 Data can only be exchanged between external memory .
Bubble sort By comparing adjacent elements in pairs , If the reverse order , That is, when the big one is in front and the small one is in the back, it will be exchanged , The small elements are swapped to the front , Until there is no reverse order , It is called bubble sort because in the sorting process , The smaller elements will float to the surface like bubbles after exchange , That is, the smallest element will go to the front of the sequence , The largest element will sink to the bottom of the sequence .
No matter how the elements are arranged in bubble sort , To contain n The list of elements needs to be traversed for bubble sorting n-1 round , The time complexity of the algorithm is O(n2), In the best case , The list is already in order and no exchange operation is required ; And in the worst case , Each comparison will result in an exchange .
The program code for bubble sorting is as follows :
# Bubble sort
def BubbleSort(alist):
for passnum in range(len(alist) - 1, 0, -1): # range() The length of the list in the function is reduced by one to 0, Each cycle -1
for i in range(passnum):
if alist[i] > alist[i + 1]: # If the subscript in the list is i The element of is greater than the subscript i+1 The elements of , Then perform the following operations to exchange two variables
temp = alist[i] # Intermediate variable temp The storage subscript is i The elements of
alist[i] = alist[i + 1] # Exchange two elements
alist[i + 1] = temp # Intermediate variable temp Assign a value to the subscript i+1 The elements of
print(alist)
BubbleSort([3, 0, 1, 9, 10, -2])
The operation results are as follows :
The specific implementation steps are as follows :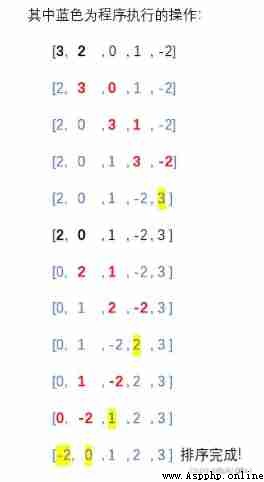
1、 because python Characteristics of , By assigning values at the same time, the exchanged three lines of statements are directly replaced by one statement :
temp = alist[i]
alist[i] = alist[i + 1]
alist[i + 1] = temp
Replace with a,b=b,a In the form of , So as to directly exchange :
alist[i], alist[i + 1] = alist[i + 1], alist[i]
def BubbleSort(alist):
for passnum in range(len(alist) - 1, 0, -1): # range() The length of the list in the function is reduced by one to 0, Each cycle -1
for i in range(passnum):
if alist[i] > alist[i + 1]: # If the subscript in the list is i The element of is greater than the subscript i+1 The elements of , Then perform the following operations to exchange two variables
alist[i], alist[i + 1] = alist[i + 1], alist[i] # Directly use a statement to exchange
print(alist)
BubbleSort([3, 0, 1, 9, 10, -2])
The operation results are as follows :
2、 Short bubbling
Bubble sorting is inefficient , Because the elements must be exchanged before the final location is determined , It iterates through the unordered parts of the list .
If no exchange occurs in a round of traversal , It indicates that the elements in the list have been ordered , At this time, the program can be terminated by modifying the program , be called Short bubble sort , Among variables passnum Control the number of cycles of the cycle , Thus, it terminates when no exchange occurs in the traversal , The code is as follows :
# Short bubble sort
def ShortBubbleSort(alist):
exchanges = True # Variable exchanges The value starts with True
passnum = len(alist) - 1 # Variable passnum The value is the length of the list minus one
while passnum > 0 and exchanges:
exchanges = False
for i in range(passnum):
if alist[i] > alist[i + 1]:
exchanges = True
alist[i], alist[i + 1] = alist[i + 1], alist[i]
passnum = passnum - 1
print(alist)
ShortBubbleSort([3, 0, 1, 9, 10, -2])
The operation results are as follows :
Selection sort Each time the list is traversed, only one exchange is made , Find the maximum value at each iteration , And put it in the right place after traversing . If given n Order of elements , Need to traverse n-1 round , This is because the last element is going to n-1 After the wheel traverses, it is in place , The time complexity of the algorithm is also O(n2).
The code for selecting sorting is as follows :
# Selection sort
def SelectSort(alist):
for i in range(len(alist) - 1, 0, -1): # range() The length of the list in the function is reduced by one to 0, Each cycle -1
positionOfMax = 0
for location in range(1, i + 1): # Exchange every time you traverse the list
if alist[location] > alist[positionOfMax]:
positionOfMax = location
alist[i], alist[positionOfMax] = alist[positionOfMax], alist[i]
print(alist)
SelectSort([9, 12, 0, -6, 7, 36, 1])
The operation results are as follows :
The specific implementation steps are as follows :
By comparing bubble sort with selection sort , Sort list [9, 12, 0, -6, 7, 36, 1], Choosing to sort only swaps 5 Time , And bubble sort up to a dozen times , Therefore, choosing a sorting algorithm is usually faster .
Insertion sort The principle of is to maintain an ordered sublist at one end of the list , Put the elements on the other side one by one Insert To this ordered list , Each round compares the current element with the elements in the ordered sublist , An ordered sublist moves its elements to the right , When it is smaller or reaches the end of the sublist , Insert the current element , Finally, make the whole list orderly , The time complexity of insertion sorting is also O(n2).
The code for inserting sorting is as follows :
# Insertion sort
def InsertSort(alist):
for index in range(1, len(alist)): # for The number of cycles is 1 Length to list -1
currentvalue = alist[index]
position = index
while position > 0 and alist[position - 1] > currentvalue:
alist[position] = alist[position - 1]
position = position - 1
alist[position] = currentvalue
print(alist)
print(InsertSort([2, 0, 9, -3, 1, 4]))
The operation results are as follows :
The specific implementation steps are as follows , The numbers marked in red on the left are arranged in good order :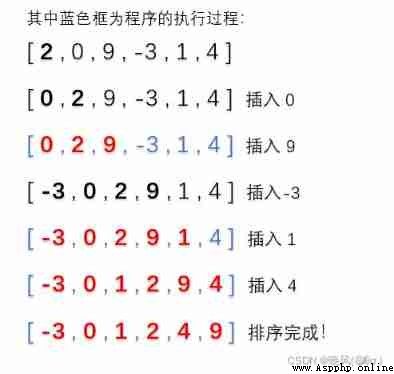
Shell Sort It is a sort algorithm improved by inserting sort , It splits the sorted list into multiple sub lists , Then insert and sort each sub list , Where the shard list uses an increment ( Or step size ) Select elements with a certain increment interval to form a sub list , Increment of sublistcount = len(alist) // 2, Then reduce the increment to sublistcount = sublistcount // 2 Continue to slice the list , Finally, the increment at this time is 1 To insert and sort .
The time complexity of Hill sort using the following code is O(n1) to O(n2) Between , The program code for Hill sorting is as follows :
# Shell Sort
def ShellSort(alist):
sublistcount = len(alist) // 2 # Select in increments of the length of the list 2 Division of , Segmentation list
while sublistcount > 0:
for startposition in range(sublistcount):
InsertSort(alist, startposition, sublistcount)
print(" Currently selected increment :", sublistcount, " Current list order :", alist)
sublistcount = sublistcount // 2 # Continue to slice the list
def InsertSort(alist, start, gap): # Insertion sort
for i in range(start + gap, len(alist), gap):
currentvalue = alist[i]
position = i
while position > 0 and alist[position - gap] > currentvalue:
alist[position] = alist[position - gap]
position = position - gap
alist[position] = currentvalue
ShellSort([2, 0, 9, -3, 1, 4])
The operation results are as follows :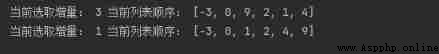
The specific implementation steps are as follows :
Merge sort It's a recursive algorithm , Each operation divides the current list into two Split , If the separated sublist is empty or has only one element , It can be considered as orderly ; If the sub list is not empty, the list will be divided into two , Recursively call merge sort on both parts , Go ahead one by one , When the list of two molecules divided into two parts is ordered , And then Merger For a sequence table , That is to finish sorting .
The time complexity of merging and sorting is O(nlogn), But the merging process requires additional storage space , The program code for merging and sorting is as follows :
# Merge sort
def MergeSort(alist):
print(" segmentation ", alist)
if len(alist) > 1: # If the length of the list is greater than 1 Then execute the following code
mid = len(alist) // 2 # Split the current list in two
left_half = alist[:mid] # The split left sub list
right_half = alist[mid:] # The right sub list of the split
MergeSort(left_half) # Recursively call its own function
MergeSort(right_half) # Recursively call its own function
i, j, k = 0, 0, 0
while i < len(left_half) and j < len(right_half): # Merge the split list into a sequential table
if left_half[i] < right_half[j]:
alist[k] = left_half[i]
i = i + 1
else:
alist[k] = right_half[j]
j = j + 1
k = k + 1
while i < len(left_half):
alist[k] = left_half[i]
i = i + 1
k = k + 1
while j < len(right_half):
alist[k] = right_half[j]
j = j + 1
k = k + 1
print(" Merger ", alist)
MergeSort([2, 0, 9, -3, 4, 1])
The operation results are as follows :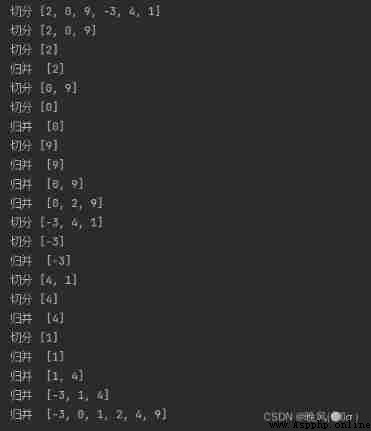
The specific implementation steps are as follows :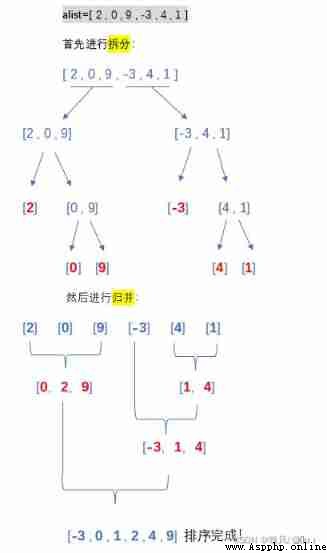
Just like merge sort , Quick sort also uses the method of dividing one into two , But it doesn't take up extra storage space , However, the list may not be split in two to affect efficiency .
First , Quick sort selects a benchmark value to be used to segment the list , That is, the separation point ; And then partition , Place elements larger than and smaller than the reference value on both sides , among leftmark and rightmark Variables represent the beginning and end elements of all remaining elements in the list .
The quick sort program code is as follows :
# Quick sort
def quickSort(alist):
quickSortHelper(alist, 0, len(alist) - 1)
print(alist)
def quickSortHelper(alist, first, last): # Recursive function
if first < last:
splitpoint = partition(alist, first, last)
quickSortHelper(alist, first, splitpoint - 1)
quickSortHelper(alist, splitpoint + 1, last)
def partition(alist, first, last): # Partition function
pivotvalue = alist[first]
leftmark = first + 1
rightmark = last
done = False
while not done:
while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
leftmark = leftmark + 1
while alist[rightmark] >= pivotvalue and rightmark >= leftmark:
rightmark = rightmark - 1
if rightmark < leftmark:
done = True
else:
alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]
alist[first], alist[rightmark] = alist[rightmark], alist[first]
return rightmark
quickSort([2, 7, -1, 0, 9, -3, 4, 1])
The operation results are as follows :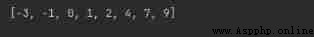
The specific implementation steps are as follows :