Blue Bridge Cup algorithm training digital game Python 90 points

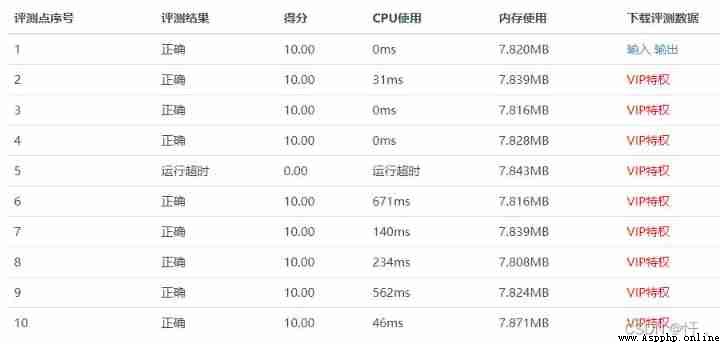
“ Add two adjacent numbers ” Get the next number , A typical Yanghui triangle . Yang Hui triangle No 4 Layer for ：contribute = [1, 3, 3, 1]

Record output weight = [3, 1, 2, 4], With the knowledge of Linear Algebra ：contribute @ weight.T = 16

So the basic idea is ：

1. Use integers n Find out Yang Hui's triangle number n layer , Write it down as contribute
2. Start enumerating from the sequence with the smallest dictionary order , Verify that the output meets the conditions

Using the property that every number in Yanghui triangle is a combinatorial number , Write this function to find contribute

def Pascal_triangle(num):
""" Yang hui triangle """
basic = 1
cont = [basic]
ele, is_even = divmod(num + 1, 2)
# ele Is the boundary of non repeating elements
for idx in range(1, ele):
basic *= (num - idx) / idx
cont.append(round(basic))
if is_even:
mirror = reversed(cont)
# Even number line : There is no need to go back
else:
mirror = reversed(cont[:-1])
# Odd line : Need to go back
cont.extend(mirror)
return cont

num On behalf of the n layer

The dictionary order is initialized to ：list(range(1, n + 1)), The function to find the next lexicographic order is ：

def next_permutation(seq):
""" Find the next dictionary order
exp: 8 3 7 6 5 4 2 1
| | """
n = len(seq)
left = -1
for idx in range(n - 2, -1, -1):
if seq[idx] < seq[idx + 1]:
# Find the right boundary of the sequence area
left = idx
break
if left != -1:
left_val = seq[left]
for right in range(n - 1, left, -1):
right_val = seq[right]
if left_val < right_val:
# Find the swap bit
seq[left] = right_val
seq[right] = left_val
seq[left + 1:] = reversed(seq[left + 1:])
# Reverse order
return seq

With [8, 3, 7, 6, 5, 4, 2, 1] For example , What this function does is ：

1. Search from right to left , because 3 < The first number on the right , So remember 3 The index of is left
2. Find the ratio from right to left 3 Large number , obtain 4 The index of is marked as right
3. In exchange for left and right The corresponding number , At this point, the sequence becomes [8, 4, 7, 6, 5, 3, 2, 1]
4. You can see left The right side is in reverse order ( namely 4 The right side of the ), So reverse seq[left + 1: ] obtain [8, 4, 1, 2, 3, 5, 6, 7]

With this function, you can enumerate the output , Each output is marked as weight. Because the blue bridge cup does not support numpy Of , So use this function to verify ：

def cal(order):
return sum([m * n for m, n in zip(order, contribute)]) == summary

 90 Good score , end