Ternary subsequence python with increasing force deduction -- greed

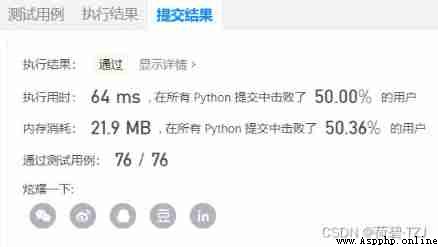
  Uncomfortable , Recently, it's really dynamic planning. When you see a problem, you think about dynamic planning first . I don't have the habit of analyzing time complexity , But today, when I saw the test example of Li Kou, I realized , want Analyze the worst time complexity

The idea of dynamic planning refers to “ The longest increasing subsequence ”, Use a one-dimensional list to record the status ,dp[n] Express nums[: n+1] The longest increasing subsequence length of , When you get the length > 3 Exit from time

Now given nums length n ( The scale of the problem ),if The statement will execute about 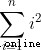 , Time complexity O()

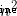class Solution(object):
def increasingTriplet(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
dp = [1 for _ in range(len(nums))]
for cur in range(1, len(nums)):
cur_num = nums[cur]
# Record cur The number pointed to by the pointer
for last in range(cur):
if nums[last] < cur_num:
# When : last The number of the pointer < cur The number of the pointer
dp[cur] = max([dp[cur], dp[last] + 1])
# State shift
if dp[cur] >= 3:
return True
return False

The sample given by the test is very long , The assumption is [1, 2] * 4000 Well , The running time is 3.65 s

The greedy idea is ： use p1 Points to the minimum value of the searched area , use p2 Points to the minor value of the searched area , These two values don't need to be in order

class Solution(object):
def increasingTriplet(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
if len(nums) < 3:
return False
p1 = nums[0]
p2 = 1 << 32
# keep p1 < p2
for p3 in nums[1:]:
if p1 < p2 < p3:
return True
if p3 > p1:
p2 = min([p2, p3])
# p2 Take the minor value
else:
p1 = p3
# p1 Minimum value
return False

With [7, 6, 3, 4, 1, 2, 5] As an example, let's push it again

Each read , Will choose Output 、 change p1、 change p2, That is to say p1 and p2 Will not change at the same time

1. change p1 when ,p1 It will only become a smaller value , Still satisfied p1 < p2, When p2 < p3 The correct results can still be output
2. change p2 when , Judgment required p3 > p1,p2 take min([p2, p3]), here p3 It must be in the position p1 after , That is, after the change p2 It must be p1 after
3. Numerically ：p1 < p2 Hang up ; position ： There must be x Satisfy p1 < x < p2,x The position of is p2 front

The worst time complexity is from dynamic programming O(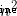) Down to the present O(n), nudges