Blue Bridge Cup [11th finals] supply Python 20 points

Although only 20 branch , But because thinking is more important , Or decided to record

This question n The data scale of is [1, 20], So the idea is chart + State compression

First read the input , The adjacency matrix of this graph is obtained

from math import inf
num, limit = map(int, input().split())
loc = [list(map(int, input().split())) for idx in range(num)]
# Record the coordinates of each vertex
adj = [[inf for _ in range(num)] for __ in range(num)]
# Initialize adjacency matrix
for begin in range(num):
x_b, y_b = loc[begin]
for end in range(begin + 1, num):
x_e, y_e = loc[end]
value = ((x_b - x_e) ** 2 + (y_b - y_e) ** 2) ** 0.5
# Calculated distance
if value <= limit:
adj[begin][end] = adj[end][begin] = value
# If the distance allows, the adjacency matrix is filled directly 

Use binary numbers to represent passing places . Such as 0000 It means to stay at the starting point ( The first 1 Locations ) Not passing through any place ,0010 It means starting from the starting point and passing through the 2 Locations ,1111 It means starting from the starting point and passing through the 2、3、4 Place and return to the starting point . Now according to “ Passing through several places ” Hierarchical binary states

bin Function to convert an integer to a binary string , Such as ：5 -> "0b101". Defined function count_1 Get the number of places you pass n, Then, the bit operation is used to screen out all the contents 1 Status of sites . Suppose there are 4 Locations , Because the first 1 A place is the last to arrive , So the final state should be 1111 (15), namely (1 << 4) - 1, Put this state on the last level

def count_1(num):
return bin(num).count("1")
dp = [{} for _ in range(num + 1)]
# The index for n The dictionary record of has passed the starting point and n Status of sites
for choose in range(1 << num):
if not choose & 1:
# Filter out all states that contain starting points
dp[count_1(choose)][choose] = inf
dp[-1][(1 << num) - 1] = inf
# Add a state containing the starting point at the last level
dp[0][0] = 0
# Initialization start state 

When creating the adjacency matrix, it has been ensured that the distance of a single flight of the aircraft will not exceed the limit , But this makes it necessary to consider that a certain place has been passed many times during the state transition 、 State transitions are too cumbersome . So use it Floyd The algorithm deals with the adjacency matrix , Find the shortest path of multiple sources

def Floyd():
for mid in range(num):
for begin in range(num):
for end in range(begin + 1, num):
state = min([adj[begin][end], adj[begin][mid] + adj[mid][end]])
adj[begin][end] = adj[end][begin] = state
Floyd()
# Find the shortest path of multiple sources 

I remember that the tutorial I read used three-dimensional matrix , But I don't think it's necessary , Just do it directly on the adjacency matrix . The author is not just , I can't say why

Use a one-dimensional list stay Record the corresponding dwell point for each state , You can do state transition layer by layer

stay = [num for _ in range(1 << num)]
# Record the final dwell point corresponding to each state
stay[0] = 0
for count in range(1, num + 1):
for last_choose in dp[count - 1]:
# Traverse the previous state
last_dist = dp[count - 1][last_choose]
# The distance corresponding to the previous state
begin = stay[last_choose]
# The dwell point of the previous state is recorded as begin
if last_dist < inf:
for cur_choose in dp[count]:
# Traverse the current state
if last_choose | cur_choose == cur_choose:
# State transition is legal
cur_dist = dp[count][cur_choose]
new = len(bin(cur_choose - last_choose)[2:]) - 1
# The current status dwell point is recorded as new
state = last_dist + adj[begin][new]
# The distance corresponding to the current state
if state < cur_dist:
# Compare and take the best
stay[cur_choose] = new
dp[count][cur_choose] = state

last_choose ( Binary status ) Taken from the dp[count-1],cur_choose Taken from the dp[count], Therefore, the number of places that have passed must meet ：cur_choose - last_choose == 1. hypothesis last_choose yes 0010,cur_choose yes 0101, utilize last_choose | cur_choose == cur_choose This condition can screen out this illegal state transition

hypothesis last_choose yes 0010,cur_choose yes 0110,cur_choose - last_choose = 0100, use len(bin(cur_choose - last_choose[2:])) - 1 You can find the index of the new passing places

Finally, the only state value of the last layer is output

result = dp[-1].popitem()[1]
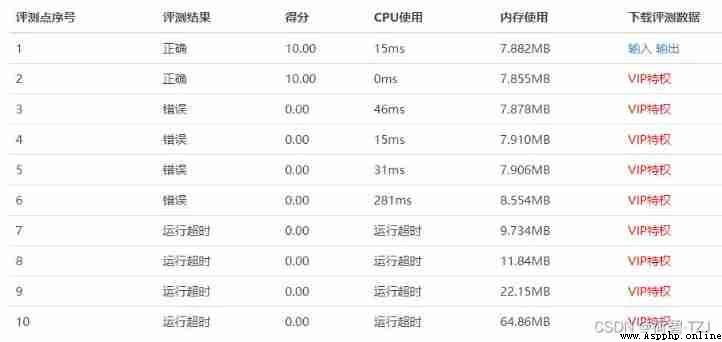
print(f"{round(result, 2):.2f}")

The train of thought looks ok , It would be great if a kind-hearted person proofread the evaluation data —— Please correct me