Recently, I wrote this question on the official website of brush force button , Because I applied for the Blue Bridge Cup , So I will write some solutions selectively ( Does not include too simple 、 It's too hard 、 Not in the scope of my examination )

The following are all questions that I think are worth thinking about  

character string

 1. Verify the palindrome string

This question mainly uses ASCII code , Write a check Function to filter out numbers 、 english , Write a casefold The function converts letters to lowercase , Then there is the double pointer comparison

Speed ：map / filter > for > while

class Solution(object):
def isPalindrome(self, s):
def check(asc):
return 97 <= asc <= 122 or 65 <= asc <= 90 or 48 <= asc <= 57
# Use ASCII Code to judge numbers 、 english
def casefold(asc):
if asc <= 90:
asc += 32
return asc
# utilize ASCII Code for lowercase conversion
s = map(ord, s)
# Convert all characters to ASCII code
s = tuple(map(casefold, filter(check, s)))
# Filter out numbers 、 english , And convert English to lowercase
if s:
sum_ = len(s) - 1
# Index sum of two pointers
for begin in range(len(s) // 2):
end = sum_ - begin
if s[begin] != s[end]:
return False
return True
else:
return True

2. Split palindrome string

  The basic idea is ：

• Whether all substrings are palindrome strings is obtained by dynamic programming bool
• Recursive function search feasible solution

Initializes a square matrix whose length and width are both string lengths dp, The first dimension represents the starting point begin, The second dimension represents the end point end, Such as dp[2][4] Express s[2: 4 + 1] Whether it is palindrome string , The value rules in this square matrix are as follows ：

• When begin == end, That is, the substring has only 1 Characters ,dp[begin][end] = True
• When end - begin == 1, That is, the substring has 2 Characters ,dp[begin][end] Taken from the s[begin] == s[end]
• When end - begin >= 2, That is, the substring is more than 2 Characters ,dp[begin][end] Taken from the dp[begin + 1][end - 1] And s[begin] == s[end]

class Solution(object):
def partition(self, s):
dp = [[False for _ in s] for _ in s]
for begin in range(len(s) - 1):
dp[begin][begin] = True
dp[begin][begin + 1] = s[begin] == s[begin + 1]
dp[len(s) - 1][len(s) - 1] = True
# initialization end - begin <= 1 The palindrome string of bool
for pace in range(2, len(s)):
# Enumerate substring steps
for begin in range(len(s)):
for end in range(begin + pace, len(s)):
dp[begin][end] = s[begin] == s[end] and dp[begin + 1][end - 1]
# Whether it is palindrome string : The substring is a palindrome string and Both characters are the same 

Last dp The effective value in the square matrix is only the upper triangle ( namely begin <= end)

 result = []
def DFS(begin, state):
if begin == len(s):
# That is, the end has been reached
result.append(state)
else:
for end in range(begin, len(s)):
if dp[begin][end]:
DFS(end + 1, state[:] + [s[begin: end + 1]])
DFS(0, [])
return result

Join the search for feasible solutions , It's done.

3. Word splitting

  The first time I did it, I used recursion , because Too much backtracking leads to timeout , So we use dynamic programming

First initialize the one-dimensional list dp, Whether the record can start with the corresponding index ,dp[3] Express s[:3] Have been combined by words , New words can be combined from this position

class Solution(object):
def wordBreak(self, s, wordDict):
wordDict = set(wordDict)
dp = [False for _ in range(len(s) + 1)]
dp[0] = True
max_len = max(list(map(len, wordDict)))
# Maximum word length
for begin in range(len(s)):
if dp[begin]:
# When this position can be used as the starting point of a word
for pace in range(1, max_len + 1):
# Enumeration substring length ( No longer than the maximum length of the word )
end = begin + pace
if end <= len(s) and s[begin: end] in wordDict:
# The destination is legal 、 The substring is the word
dp[end] = True
return dp[-1]

dp[-1] namely dp[len(s)], Index representation len(s) Whether it can be used as the starting point of a word , That is the final answer

4. Word splitting Ⅱ

Little knowledge ：Python Inside list It's a sequential storage structure ,set Is a hash table storage structure , Search aspect set faster , But the occupied space is relatively high

Because of this wordDict The longest is 1000, So it is necessary to change it into set. a move DFS The game is over

class Solution(object):
def wordBreak(self, s, wordDict):
wordDict = set(wordDict)
max_len = max(list(map(len, wordDict)))
# Maximum word length
result = []
def DFS(begin, state):
if begin == len(s):
result.append(" ".join(state))
else:
for pace in range(1, max_len + 1):
# Enumeration substring length
end = begin + pace
if end <= len(s) and s[begin: end] in wordDict:
# The destination is legal 、 The substring is the word
DFS(end, state[:] + [s[begin: end]])
DFS(0, [])
return result

5. Implement prefix tree

Inherit dict Type to write a class , Rewrite it __getitem__, The function of this rewriting is ：trie["a"] When the corresponding value cannot be found , It won't report mistakes like a dictionary , It's going back to None

class Trie(dict):
end_of_word = "#"
""" Prefix tree """
def __init__(self):
super(Trie, self).__init__()
# call dict Of __init__()
def __getitem__(self, item):
return self.get(item, None)
def insert(self, word):
head, *tail = word
tar_node = self[head]
# Try to search the next node
if not tar_node:
tar_node = Trie()
self[head] = tar_node
if tail:
tar_node.insert(tail)
else:
tar_node[self.end_of_word] = True
def search(self, word):
head, *tail = word
next_ = self[head]
# Try to search the next node
if next_ is not None:
return next_.search(tail) if tail else bool(next_[self.end_of_word])
# If there is a tail, continue to search , If there is no tail, find the word Terminator
else:
return False
def startsWith(self, word):
head, *tail = word
next_ = self[head]
# Try to search the next node
if next_ is not None:
return next_.startsWith(tail) if tail else True
# If there is a tail, continue to search , If there is no tail, it returns True
else:
return False

  Let's test it ：

tree = Trie()
tree.insert("apple")
print(tree)
print(tree.search("app"), tree.search("apple"))

{'a': {'p': {'p': {'l': {'e': {'#': True}}}}}}
False True 

Not very good in terms of speed

Array

1. Product maximum subarray

The idea of this question is a bit like the previous one Split palindrome string . Initialize the two-dimensional square matrix , The first dimension represents the starting point of an interval , The second dimension represents the end point of the interval ,dp[begin][end] Represents the starting point begin End end The interval product of . Because the starting point begin and End end Satisfy ：begin <= end, So the effective region of the final matrix is the upper triangle

class Solution(object):
def maxProduct(self, nums):
dp = [[0 for _ in range(len(nums))] for _ in range(len(nums))]
max_ = max(nums)
# Interval starting point 、 The maximum value at which the end points are consistent
for begin in range(len(nums) - 1):
end = begin + 1
value = nums[begin] * nums[end]
max_ = max([value, max_])
dp[begin][end] = value
# initialization end - begin == 1 Part of
for pace in range(2, len(nums)):
# enumeration end - begin Value
for begin in range(len(nums) - 1):
end = begin + pace
if end < len(nums):
# When the end position is legal
value = dp[begin][end - 1] * nums[end]
max_ = max([value, max_])
dp[begin][end] = value
# Fill in interval product data
return max_

The test pass rate of this code is 98.4 %, Finally, it got stuck in a length 15000 Example . I think the optimization direction is the storage of the upper triangular matrix , But this 98.4 % I have satisfied the passing rate of

 2. Most elements  

This question uses the Moore voting method ：

Suppose that each different number in the array represents a country , The number of numbers represents the number of people in this country , They scuffled together , That is, every two two die together . We can know that the one whose number is more than half the length of the array will win .

Even if we take tenthousand steps back , Everyone else has come to attack this country with the largest number of people , Every two of them died together , What is left is the mode .

author ： Data structures and algorithms
https://leetcode-cn.com/leetbook/read/top-interview-questions/xm77tm/?discussion=POk1ka

  With reference to the idea of two people dying together , The code is simple

class Solution(object):
def majorityElement(self, nums):
major = nums[0]
count = 1
# Take out No 1 Elements as the main force
for new in nums[1:]:
if new == major:
count += 1
# The number of +1
elif count == 0:
major = new
count = 1
# Change the main faction
else:
count -= 1
# Dry turn 1 people
return major

3. Increasing ternary subsequences

  Use greedy thinking to do , It is a very valuable question for me , Specially written in another article ：

Power button Increasing ternary subsequences Python —— greedy https://hebitzj.blog.csdn.net/article/details/122789370

4. Search for a two-dimensional matrix

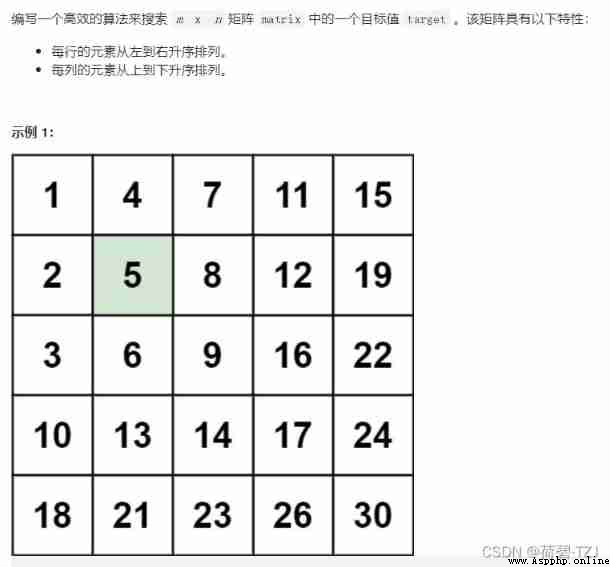
  According to the idea of dichotomy , Find a position where you can jump left and right , That is, the upper right corner or the lower left corner —— Take the upper right corner as an example ：

  Current value value Initialize to the upper right corner , And target value target Compare ：

• if value > target, Move left
• if value < target, Then move down
• if value == target, Then return to True
• If you move out of bounds , Then return to False

class Solution(object):
def searchMatrix(self, matrix, target):
rows = len(matrix)
cols = len(matrix[0])
row_ = 0
col_ = cols - 1
value = matrix[row_][col_]
while value != target:
if value > target:
col_ -= 1
# Search left
else:
row_ += 1
# Search down
if col_ < 0 or row_ >= rows:
return False
value = matrix[row_][col_]
return True

 5. Merge two ordered arrays

Initialize two pointers p1、p2, And point to the tail of the two arrays , Compare the number corresponding to the pointer , And then from nums1 Start inserting numbers after —— Add one blank Indicate the insertion position . With nums1 = [2, 4, 6, 0, 0, 0],nums2 = [1, 3, 7] For example

p1p2blanknums1225[2, 4, 6, 0, 0, 7]214[2, 4, 6, 0, 6, 7]113[2, 4, 6, 4, 6, 7]012[2, 4, 3, 4, 6, 7]001[2, 2, 3, 4, 6, 7]-100[1, 2, 3, 4, 6, 7]-1-1-1[1, 2, 3, 4, 6, 7]

The sign of the end of the consolidation process is p2 < 0. When comparing the value of the corresponding position of the pointer , consider p1 < 0 That's it

class Solution(object):
def merge(self, nums1, m, nums2, n):
p1 = m - 1
p2 = n - 1
blank = p1 + n
while p2 >= 0:
# That is to say, it has not been consolidated
if p1 < 0 or nums2[p2] >= nums1[p1]:
# Be careful p1 < 0 The situation of
nums1[blank] = nums2[p2]
p2 -= 1
else:
nums1[blank] = nums1[p1]
p1 -= 1
blank -= 1

Pile up 、 Stack and queue

1. Median in data stream

  The initial sequence is an empty column , The basic idea of this question is ：

• Every time you add an integer , Take turns to join Big root pile 、 Heap , The purpose is to maintain the difference between the nodes of two heaps <= 1
• The characteristic of large root heap is that the value of root node is the largest , The same goes for small root piles . When the root node value of the large root heap <= The root node value of the small root heap , The elements in the large root heap are the first half of the ordered sequence , The elements in the small root heap are the last half of the ordered sequence
• When you need to find the median , Adjust to   The root node value of the large root heap <= The root node value of the small root heap , Then you know how to do it

Python Provides a standard library of small root heaps (heapq), The use details are as follows ：

heapify(seq)

In situ small root stacking

heappush(heap, ele)

Add heap nodes

heappop(heap)

Eject the top of the pile , And rearrange

nsmallest(n, seq)

Back before ascending n Elements

nlargest(n, seq)

Return to before descending n Elements

import heapq
class Min_Heap(list):
""" Heap """
def __init__(self, seq):
super(Min_Heap, self).__init__(seq)
heapq.heapify(self)
# Heap the elements in place
def push(self, ele):
# Elements into the heap
heapq.heappush(self, ele)
def poproot(self):
# Pop up the top elements and rearrange
return heapq.heappop(self)

Heap is a complete binary tree structure , So just use list Storage . This library actually has functions with large root heap , But the function is not complete , Function names are also hidden , Therefore, it is not recommended to directly call . If the function of the small root heap is used to make the large root heap , Is that every element is negated ：push and pop Plus a minus sign

import heapq
class Max_Heap(list):
""" Big root pile """
def __init__(self, seq=[]):
super(Max_Heap, self).__init__(self._negative(seq))
heapq.heapify(self)
def push(self, ele):
# Elements into the heap
heapq.heappush(self, - ele)
def poproot(self):
# Pop up the top elements and rearrange
return - heapq.heappop(self)
def _negative(self, seq):
# Numerical inversion
return map(lambda x: -x, seq)
def value(self):
return list(self._negative(self))

The test code is annotated in great detail , Look directly at ：

import heapq
class MedianFinder(object):
def __init__(self):
self.max_heap = []
self.min_heap = []
self._flag = True
def addNum(self, num):
"""
:type num: int
:rtype: None
"""
num = float(num)
if self._flag:
# That is, the length of large root heap and small root heap are equal
heapq.heappush(self.max_heap, -num)
# The new element -> Big root pile
self._flag = False
else:
# Number of large root heap nodes - Number of small root nodes == 1
heapq.heappush(self.min_heap, num)
# The new element -> Heap
self._flag = True
def findMedian(self):
"""
:rtype: float
"""
if self.min_heap:
# Make sure that the small root heap is not empty
while - self.max_heap[0] > self.min_heap[0]:
pop = - heapq.heappop(self.max_heap)
heapq.heappush(self.min_heap, pop)
# Big root pile top -> Heap
pop = - heapq.heappop(self.min_heap)
heapq.heappush(self.max_heap, pop)
# The top of the pile -> Big root pile
if self._flag:
# That is, the length of large root heap and small root heap are equal
return (- self.max_heap[0] + self.min_heap[0]) / 2
else:
return - self.max_heap[0]

Originally, it has been overtime —— But after modification 、 When submitting the last time , I didn't think of

2. In order matrix k Small elements

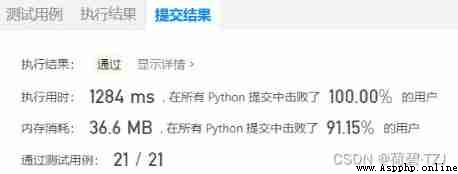
  There's a train of thought that I don't think is very useful in this problem , But I still feel it necessary to say

   Assuming that a given 9 * 9  Matrix , Before speculation 9  The distribution of the smallest elements is found , These smallest elements always come together , From then on, we can narrow the search area to this range

• row = 1,col = k // 1 = 9, That is, it is all distributed in the first line
• row = 2,col = k // 2 = 4, That is, the first two lines are distributed separately 4 individual , The remaining 1 On the first line
• row = 3,col = k // 3 = 3, That is, the first three lines are distributed separately 3 individual
• row = 4,col = k // 4 = 2, That is, the first four lines are distributed 2 individual , The remaining 1 On the first line
• row = 5,col = k // 5 = 1, And so on

  Organize the elements of this area into a list , Then use the heap to find the target

class Solution(object):
def kthSmallest(self, matrix, k):
import heapq
row_bound = min([k, len(matrix)])
cols = len(matrix[0])
# Get the row and column search boundary
seq = []
for row in range(row_bound):
col_bound = k // (row + 1)
# Calculate the element distribution boundary
seq += matrix[row][:min([col_bound, cols])]
# The element distribution boundary is compared with the actual number of columns
result = heapq.nsmallest(k, seq)[-1]
# Before stacking k Elements : Efficiency is higher than for loop
return result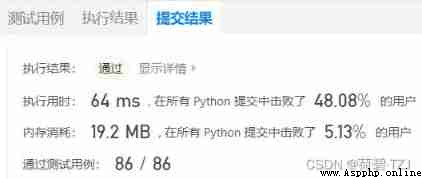

3. Basic calculator Ⅱ

  Let's start with a function ：eval(string), You can convert strings into variables return, Such as string = "2 * 3 + 2", Then we get To 8 —— So this problem can be completed in one line of code

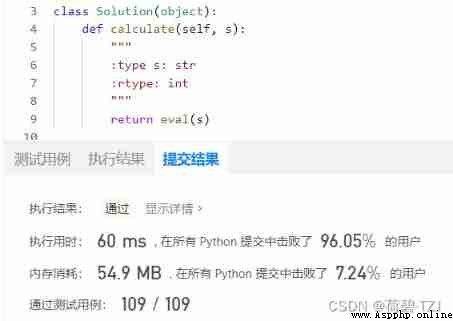
  It's about the process , Let's implement it with multiple lines of code . If a given "1 * 2 + 3"：

• Scan from scratch , Read "1 * 2" We are not sure whether we can calculate ( Suppose there is a ratio * Higher priority Operators )
• Read "1 * 2 + 3", We can be sure of 2 This number is with 1 still 3 Forget it together —— because * Has a higher priority than +, therefore Whether it can be calculated The condition is ： Priority of the previous operator >= The current operator

The only operators in this question are +、-、*、/, Consider the boundary conditions , add to Start character 、 Terminator That's all right.

class Solution(object):
def calculate(self, s):
from re import findall
s = findall(r"[+\-*/]|\d+", s) + ["$"]
# re Regular expressions : Separate numbers from operators
oper = ["#"]
num = []
# Initialize the value stack 、 Operator stack
priority = {"#": -1, "$": 0, "+": 1, "-": 1, "*": 2, "/": 2}
# Record priority : "#" Start flag , "$" End mark
for ele in s:
if ele in priority:
# Operator : Compare with the previous operator first , Calculate and then stack
while priority[oper[-1]] >= priority[ele]:
# Priority of the previous operator >= The current operator
last_oper = oper.pop()
num1 = num.pop()
num2 = num.pop()
# Pop up the number to be calculated
new = eval("{}{}{}".format(num2, last_oper, num1))
num.append(new)
# Calculate the previous combination
oper.append(ele)
else:
# Numbers : Go straight to the stack
num.append(ele)
return int(num.pop())

Sorting and Retrieval

1. The maximum number

  The second example shows ：nums = [3, 30, 34, 5, 9], The ideal sort is [9, 5, 34, 3, 30], This is similar to the result sorted by dictionary —— The result of Lexicographic sorting is [9, 5, 34, 30, 3], stay Python It converts all elements into character classes , After sorting, you can get the result close to the answer , Take advantage of this feature of character types , To make a small adaptation of the character class

class Solution:
def largestNumber(self, nums):
class new_str(str):
def __le__(self, other):
return self + other <= other + self
# encounter <= Operator
def __ge__(self, other):
return self + other >= other + self
# encounter >= Operator
def __lt__(self, other):
return self + other < other + self
# encounter < Operator
def __gt__(self, other):
return self + other > other + self
# encounter > Operator
nums = map(new_str, nums)
result = "".join(sorted(nums, reverse=True))
return str(int(result))

Original "9" and "30" The comparison is direct "9" > "30", Now it is "930" > "309", obtain "9" > "30"

Original "3" and "30" The comparison is direct "3" < "30", Now it is "330" > "303", obtain "3" > "30", To achieve an end

Dynamic programming

1. There are at least k The longest substring of repeated characters

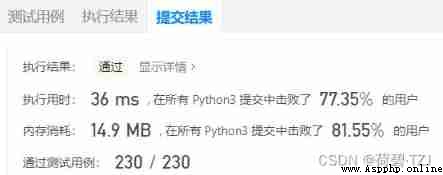
The substring is continuous , Subsequences are discontinuous . This question is in Chinese Counter To do it , Use a one-dimensional list dp To store state , Such as dp[idx] End point idx ( The starting point is unknown ) Substring Counter

The basic steps of the code are as follows ：

1. If the length of the input string < k, Go straight back to 0
2. otherwise , initialization dp,dp[idx] Express s[0: idx + 1] Of Counter ( prune ： Skip length is less than k Of ), While initializing, check whether it meets the problem conditions , Record the maximum length length
3. Enumeration substring start begin ( from 1 Start ),dp[idx] = dp[idx] - Counter(s[begin - 1]), It's the original dp[idx] yes  s[begin - 1: idx + 1] Of Counter, After updating, it becomes s[begin: idx + 1] Of Counter ——   Check whether the problem conditions are met while updating , Record the maximum length length ( prune ： Skip length is less than max([k, length]) Of )

class Solution:
def longestSubstring(self, s: str, k: int) -> int:
if len(s) < k:
return 0
else:
def check(counter):
for value in counter.values():
if value < k:
return False
return True
# Detection counter : Whether the number of occurrences of each character is >= k
from collections import Counter
dp = [None for _ in range(len(s))]
dp[k - 1] = Counter(s[:k])
if check(dp[k - 1]):
length = k
else:
length = 0
# Initialize the current maximum length
for end in range(k, len(s)):
# Ignore length less than k String
dp[end] = dp[end - 1] + Counter(s[end])
if check(dp[end]):
length = end + 1
# dp[idx]: Starting from 0、 The finish for idx The counter of the substring of
for begin in range(1, len(s) - max([k, length]) + 1):
# such as : length 6, k=3, Then there is no need to search to index 4 A substring for the starting point
# Such as begin = 1, dp[idx] Still indicates that the starting point is 1、 The finish for idx The string of
next_end = begin + max([k, length]) - 1
# hypothesis begin = 2, max([k, length]) = 4, be end Directly from 5 Start
for end in range(next_end, len(s)):
dp[end] -= Counter(s[begin - 1])
# To put begin from 1 Turn into 2, You need to dp Subtract... From each counter in s[1]
if check(dp[end]):
length = end - begin + 1
# Because always search in the best direction , So update directly
return length

After the pruning is done in place , The program will always search in a better direction , So you don't need to use max Function update length

The test pass rate is 91.4%, Finally it got stuck in a length 7801 String

2. The maximum path in a binary tree and

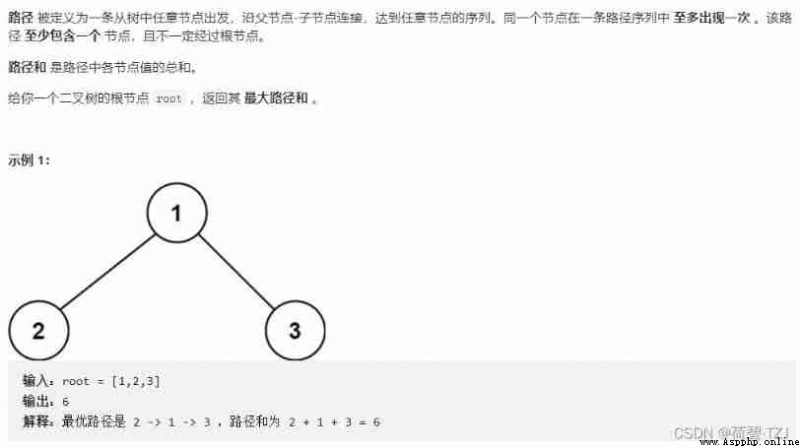
Only one inflection point is allowed for a path in a binary tree , Take each node as the inflection point , Find the maximum path sum under the inflection point —— Take the maximum path sum of all inflection points as the answer

use ReLU Function to discard negative paths and branches , Add one more DFS Function can be done

class Solution:
def maxPathSum(self, root) -> int:
def ReLU(num):
return num if num > 0 else 0
# Set the negative value to zero ( Discard negative paths and branches )
state = []
# Record the maximum path and when all nodes are used as inflection points
def DFS(node):
if node:
left = DFS(node.left)
right = DFS(node.right)
# Returns the left edge 、 The maximum path sum of the right branch ( Its value >= 0)
new = node.val + left + right
state.append(new)
# The path length with the current node as the inflection point of the path , Stored in the status list
return ReLU(max([left, right]) + node.val)
# Returns the longest Branch + The value of the node
else:
return 0
DFS(root)
return max(state)

3. raid homes and plunder houses

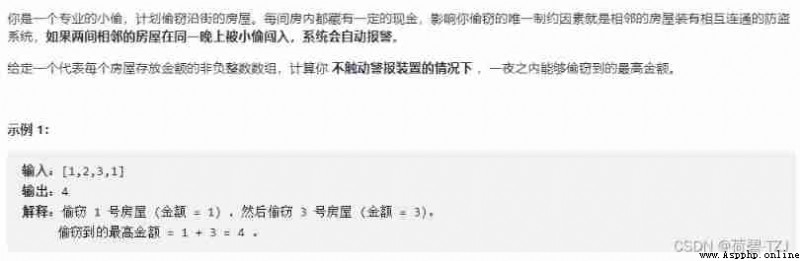
  This question is similar to the one in the Blue Bridge Cup , Refer to another article of mine for details

Blue Bridge Cup [ The first 11 The finals ] Blue jump Python 30 branch _ Hebi ·TZJ The hydrology of -CSDN Blog The score is not high , Or have the cheek to write limit, cond, length = map(int, input().split())mod = 20201114dp = [[0, 0] for _ in range(length + 1)]dp[0] = [1, 0]# Represent the : There is no limit to jumping , Skip limited read input , Then use a one-dimensional list dp To record the status ,dp[0] Represents the state at the starting point , Among them [1, 0] Represent the ：“ There is no limit to jumping ” Number of alternatives 、“ Jumping is limited ” The number of schemes for state transition is very simple , Such as ： At present ...https://hebitzj.blog.csdn.net/article/details/122799362?spm=1001.2014.3001.5502

4. Complete square

First enumerate all n The complete square within , Then save it to the list pace in . Use the idea of backpack to do , Initializes a length of n + 1 A list of bag, Such as bag[13] Represents superimposed to 13 The least square required

class Solution:
def numSquares(self, n: int) -> int:
from math import inf
pace = [num ** 2 for num in range(int(n ** 0.5) + 1)]
bag = [inf for _ in range(n + 1)]
bag[0] = 0
# Initialize knapsack and square list
for sum_ in range(n):
# Enumerate the capacity of the backpack
cur = bag[sum_]
# Minimum square required at current capacity
if cur < inf:
# The current capacity can reach
for weight in pace:
# Enumeration square
next_ = sum_ + weight
if next_ <= n:
bag[next_] = min([bag[next_], cur + 1])
# Add a number , Compare and take the best
else:
break
return bag[-1]

5. Change for

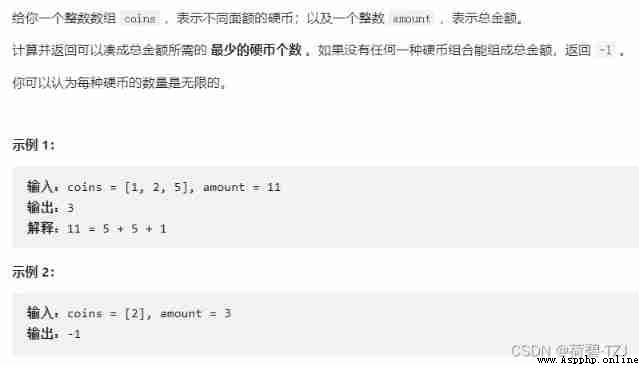
  A great question , I have a detailed discussion in another article

Power button Change for Python —— knapsack _ Hebi ·TZJ The hydrology of -CSDN Blog This problem needs a backpack . The first time I did this problem , A two-dimensional matrix is used to record the state —— The test results are touching because I changed the spatial complexity from O(mn) drop to O(n) When , While simplifying the code , The execution time has also been reduced by about half , So it is also very important to reduce the space complexity from the basic framework , Then consider the boundary conditions with a one-dimensional list bag To record the status ,bag[0] Means to fold to 1￥ The minimum number of coins required ,bag[amount - 1] Indicates the minimum number of coins needed to fold to the total amount . Because the optimal operation is min, therefore bag The initial value of inf = amount + 1...https://hebitzj.blog.csdn.net/article/details/122807809?spm=1001.2014.3001.5502

6. The longest incremental path in the matrix

chart + Memorize DFS, The basic steps are ：

1. Write a function that flattens two-dimensional coordinates into one-dimensional indexes , Preprocessing to get adjacency table
2. Initialize the memory table memory,memory[idx] Means to index idx Is the longest incremental path of the starting point
3. Memory depth first search ： While recalling useful memories , While storing new memories
4. The final answer is memory The maximum of

Not used here Floyd The reason for multi-source shortest circuit is ： This is a directed graph , And the output of each point is not greater than 4, This shows that the adjacency matrix corresponding to this graph is a sparse matrix ,Floyd The algorithm will consume a lot of unnecessary space

class Solution:
def longestIncreasingPath(self, matrix) -> int:
rows = len(matrix)
cols = len(matrix[0])
adj = [[] for _ in range(rows * cols)]
def loc2idx(row, col):
return row * cols + col
# Row column coordinates -> One dimensional index
for r in range(rows):
for c in range(cols):
idx = loc2idx(r, c)
data = matrix[r][c]
# Enumerate each cell in the matrix
for r_, c_ in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
new_r = r + r_
new_c = c + c_
# Enumerate four adjacent cells
if 0 <= new_r < rows and 0 <= new_c < cols:
next_ = matrix[new_r][new_c]
if data < next_:
next_idx = loc2idx(new_r, new_c)
adj[idx].append(next_idx)
# Add to adjacency table
memory = [0 for _ in range(rows * cols)]
# Indicates the longest incremental path under the corresponding starting point of the index
def DFS(idx):
if not memory[idx]:
# If there is no memory at this point
result = [DFS(next_) for next_ in adj[idx]]
if result:
memory[idx] = max(result) + 1
# Take the optimal path + In itself
else:
memory[idx] = 1
# Go to a dead end , The length of the incremental path starting from this point is 1
return memory[idx]
for idx in range(rows * cols):
DFS(idx)
return max(memory)

My idea is relatively clear compared with the practice of direct memorization and deep search , But at the same time, the execution time 、 There is more space . I think , During the game , Still pay attention to balance performance and Readability . High readability -> check bug Easy to , If you blindly pursue performance without considering readability , Once it's out bug It's going to take a lot of time

graph theory

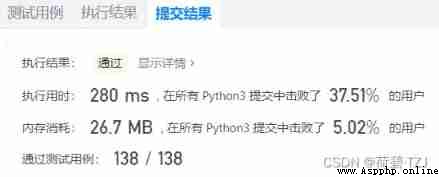
The questions given by Li Kou are very simple , As long as you know a few algorithms, you can do , I just hang up the code

1. Dijkstra Single source shortest path

from math import inf
def Dijkstra(sourse, adj):
""" Single source shortest path ( Without negative weight )
sourse: Source point
adj: Adjacency table of graph """
dist = [[inf, True] for _ in range(64)]
dist[sourse][0] = 0
while 1:
min_idx = -1
min_val = inf
for idx, (dis, flag) in enumerate(dist):
if flag and dis < min_val:
min_val = dis
min_idx = idx
# find min_idx, min_dist
if min_idx != -1:
dist[min_idx][1] = False
for idx, (dis, flag) in enumerate(dist):
if flag:
state = min_val + adj[min_idx][idx]
dist[idx][0] = min([state, dist[idx][0]])
else:
return dist

With a little modification, you can find the longest path , The reverse requires no positive rings

2. Floyd Multi source shortest path

def Floyd(adj):
""" Multi source shortest path ( With negative weight )
adj: Adjacency table of graph """
vertex_num = len(adj)
dist = adj.copy()
for pass_p in range(vertex_num):
for sourse in range(vertex_num):
for end in range(vertex_num):
attempt = dist[sourse][pass_p] + dist[pass_p][end]
dist[sourse][end] = min([dist[sourse][end], attempt])

3. A topological sort

def topo_sort(in_degree, adj):
""" AOV Network topology sorting ( Minimum dictionary order )
in_degree: On the scale
adj: The adjacency matrix of a graph """
seq = []
while 1:
visit = -1
for idx, degree in enumerate(in_degree):
if degree == 0:
visit = idx
in_degree[idx] = inf
seq.append(visit)
# Record : The degree of 0 The summit of
for out, weight in enumerate(adj[visit]):
if 0 < weight < inf:
in_degree[out] -= 1
break
if visit == -1:
break
# End of the search / Existential ring : sign out
return seq

4. Prim Minimum spanning tree

def Prim(sourse, adj):
""" Minimum spanning tree
sourse: Source point
adj: Adjacency table of graph """
low_cost = adj[sourse].copy()
last_vex = [sourse for _ in range(len(adj))]
# Record low_cost The starting point corresponding to the edge weight in
undone = [True for _ in range(len(adj))]
undone[sourse] = False
# Record whether the vertex has been used as the exit point
edges = []
while any(undone):
next_ = low_cost.index(min(low_cost))
begin = last_vex[next_]
edges.append((begin, next_))
# Find the endpoint of the edge with the lowest weight
low_cost[next_] = inf
undone[next_] = False
# Mark the point
for idx, (old, new, flag) in enumerate(zip(low_cost, adj[next_], undone)):
if flag and old > new:
# Meet better, then update
low_cost[idx] = new
last_vex[idx] = next_
return edges

5. Euler path

def Euler_path(sourse, adj, search):
""" Euler path ( Traverse each side 1 Time )
sourse: Path start
adj: Adjacency table of graph
search: Edge search function """
path = []
stack = [sourse]
while stack:
visit = stack[-1]
out = adj[visit]
# visit : Top of stack
if out:
visit, out = search(visit, out)
if out:
stack.append(visit)
# Push : The waypoint conditions have not been met
else:
path.append(visit)
# List : Meet the conditions of the approach point
else:
path.append(stack.pop(-1))
# List : Meet the conditions of the approach point
path.reverse()
return path

mathematics & An operation

 1. A number that appears only once

Two key points can be found after reading the questions ： Only one element appears only once 、 Each of the other elements occurs twice

“ Same as 0, Dissimilarity is 1”, Think of XOR immediately . All elements are XOR together , The final value is the element that appears only once

class Solution(object):
def singleNumber(self, nums):
num = nums.pop()
while nums:
num ^= nums.pop()
return num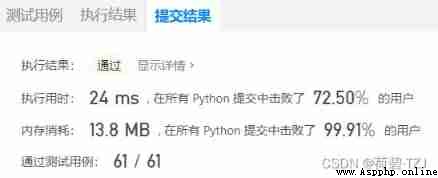

2. Zero after factorial

10 In addition to its own factors there are 1、2、5, That is, the factorial result follows 0 The number of is determined by the factor 5 Determined by the number of ( Factor 2 The number of is always greater than the factor 5 The number of ). All the factors are decomposed into several 5, As a result, there are several followers 0

class Solution(object):
def trailingZeroes(self, n):
count = 0
# Factor 5 The number of
for num in range(n, 0, -1):
while not num % 5:
# When digital analog 5 No remainder
num //= 5
count += 1
return count

although divmod Function can do the remainder division , But it takes about Division operator + The remainder operator Of 1.5 times , Not recommended

3. Count prime

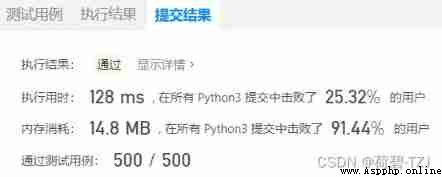
  The basic idea is , Use a one-dimensional list to record the number of prime numbers bool, Suppose every number is a prime number . Every prime number found , Just enumerate the composite numbers with it as a factor , Modify the logo

class Solution:
def countPrimes(self, n: int) -> int:
bound = int(n ** 0.5)
result = [True for _ in range(n)]
# Initializes the prime flag list
for mod in range(2, bound + 1):
if result[mod]:
# Find the prime number , And as the minimum factor
for choose in range(mod ** 2, n, mod):
result[choose] = False
# Enumerating composite numbers : Multiple of the minimum factor
return sum(result[2:])

4. Missing number  

1. An operation

The length is n, Then the number range is [0, n], Add all the numbers in this range to the array , It becomes “ Only one element appears only once 、 Each of the other elements occurs twice ”

class Solution:
def missingNumber(self, nums) -> int:
result = 0
for num in range(1, len(nums) + 1):
result ^= num
for num in nums:
result ^= num
return result

2. A sequence of equal differences

class Solution:
def missingNumber(self, nums) -> int:
n = len(nums)
sum_ = n * (n + 1) // 2
return sum_ - sum(nums)